
6 KL变换 口最小化均方误差 g)=∑平u,-∑u-1) i=d+1 i=d+l 0g(u)- uj )→(Ψ-I)u,=0,j=d+1,,0, 令d=0,有Ψu,=,uj,j=1,,0, →5=∑ j=d+1
6 K-L 变换 最小化均方误差 1 1 ( ) ( 1) T T j j j jj j d j d g u u u uu ( ) 0 ( ) 0, 1, , ; j j j g I jd u u u 0, = , 1, , ; j jj 令 有 d j u u 1 . j j d
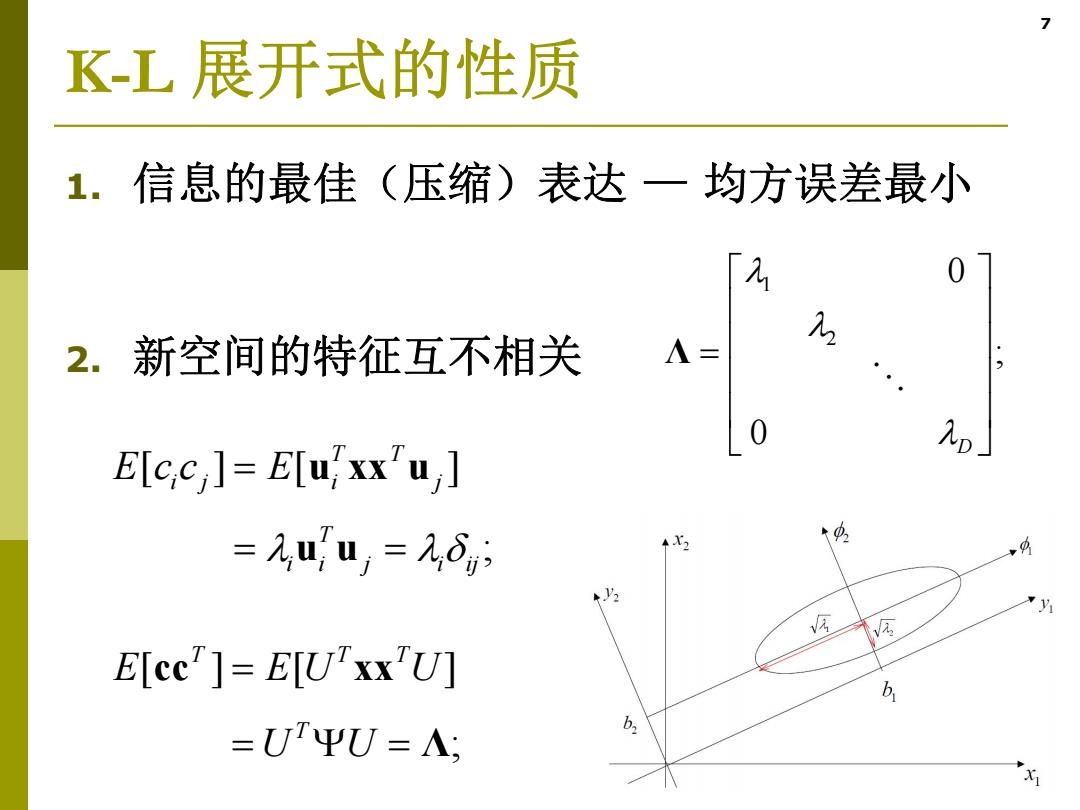
7 K-L展开式的性质 1.信息的最佳(压缩)表达一均方误差最小 0 2.新空间的特征互不相关 Λ= 0 E[c,c ]E[u;xx'u =,uu,=6 4X2 ↑ 归 E[cc"]=E[U'xx'U] 6 =UΨU=A, b 专
7 K-L 展开式的性质 1. 信息的最佳(压缩)表达 — 均方误差最小 2. 新空间的特征互不相关 [] [ ] ; T T ij i j T i i j i ij E cc E u xx u u u [] [ ] ; T TT T E EU U U U cc xx Λ 1 2 0 ; 0 D Λ

8 K-L展开式的性质 3.表示熵最小 归一化展开系数的方差(特征值入) 2,j=12,,D,→0≤,≤1,2元=1 i=1 表示熵 Ha=-2元,1log元
8 K-L 展开式的性质 3. 表示熵最小 归一化展开系数的方差(特征值λj) 表示熵 .1 ,10 ,,,2,1 , 1 1 D i j i D i i j j Dj 1 log . D j j R j H

9 KL展开式的性质 02+ FIGURE 6.1:The KL transform is not always best for pattern recognition.In this example,projection on the eigenvector with the larger eigenvalue makes the two classes coincide.On the other hand,projection on the other eigenvector keeps the classes separated
9 K-L 展开式的性质
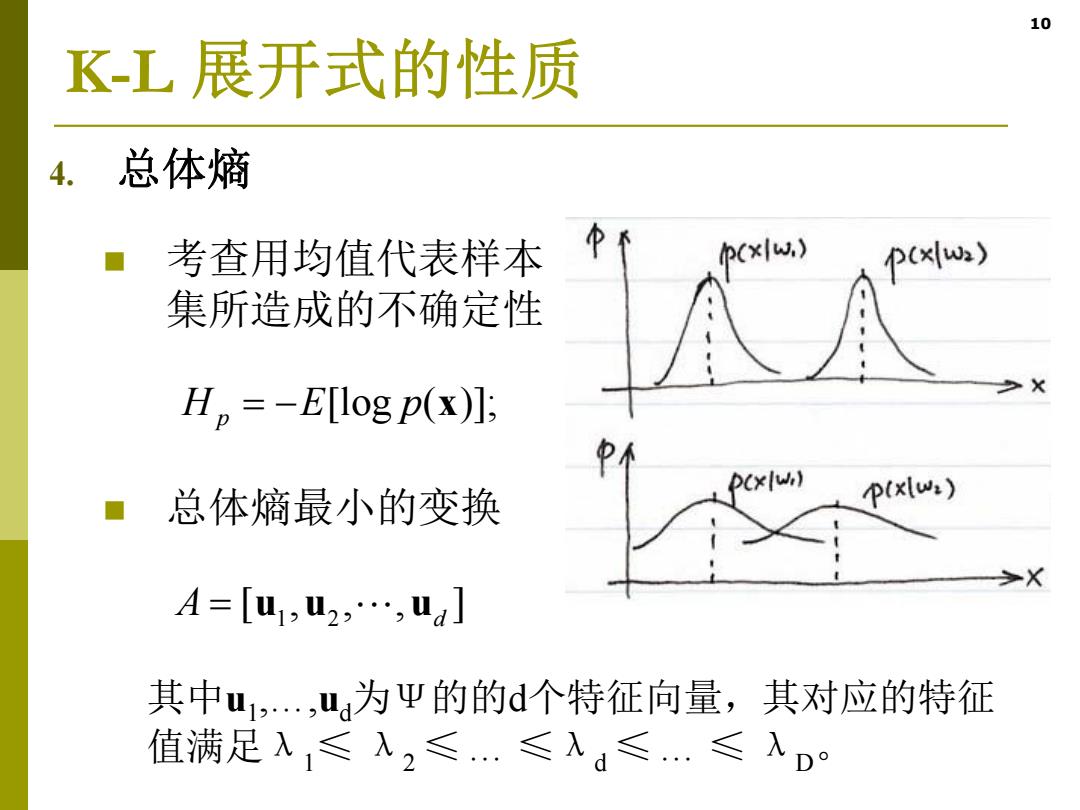
10 K-L展开式的性质 4. 总体熵 考查用均值代表样本 pcxIw.) pcx(w) 集所造成的不确定性 H。=-E[log p(x]: 总体熵最小的变换 A=[u1,u2,…,ua] 其中u1,,为Ψ的的d个特征向量,其对应的特征 值满足入,≤入2≤.≤入≤…≤入D
10 K-L 展开式的性质 4. 总体熵 考查用均值代表样本 集所造成的不确定性 总体熵最小的变换 p pEH x)];([log 1 2 [, , , ] A uu u d 其中u1 ,…,ud 为Ψ的的d个特征向量,其对应的特征 值满足λ1 ≤ λ2 ≤… ≤λd ≤… ≤ λD