For 2n Persons (n=1,2,3,...) 2n-1 -12 n persons left 假设在规模为n 的问题中,解 是m:J(n)=m m-l ?=J(2n)=2m-1=2J(n)-1
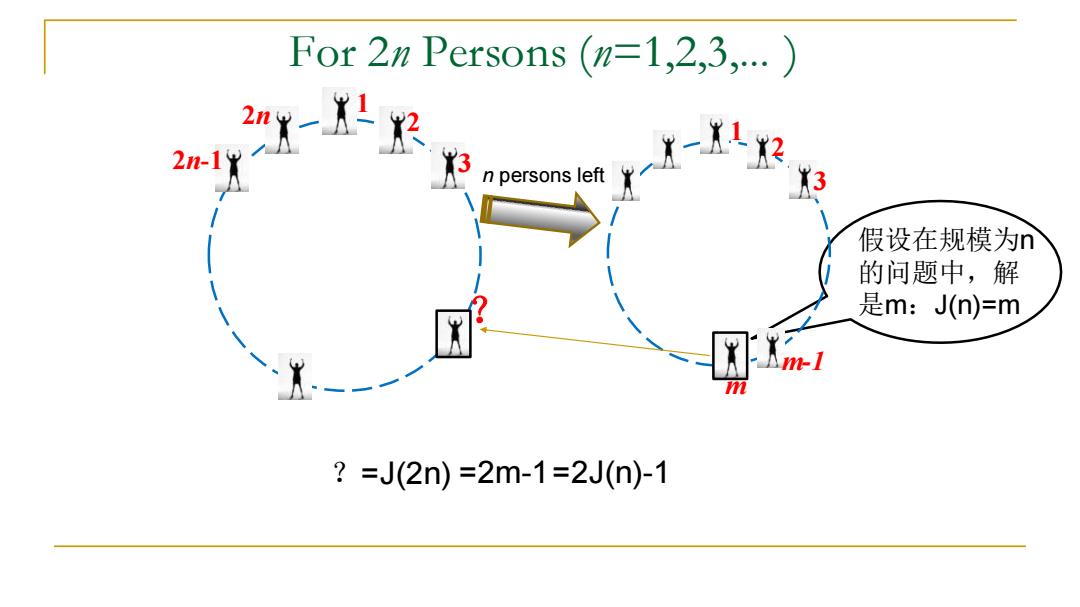
For 2n Persons (n=1,2,3,... ) 1 2n 2 2n-1 3 n persons left ?=J(2n) 假设在规模为n 的问题中,解 是m:J(n)=m 1 2 3 m m-1 ? =2m-1=2J(n)-1
And What about 2n+1 Persons (=1,2,3,... m- 2n 2+y-35 2n-1X do the same: n persons left i- k+1 The smaller problem's solution is:J(n) And the solution of the original problem 2n+1 is 2+1
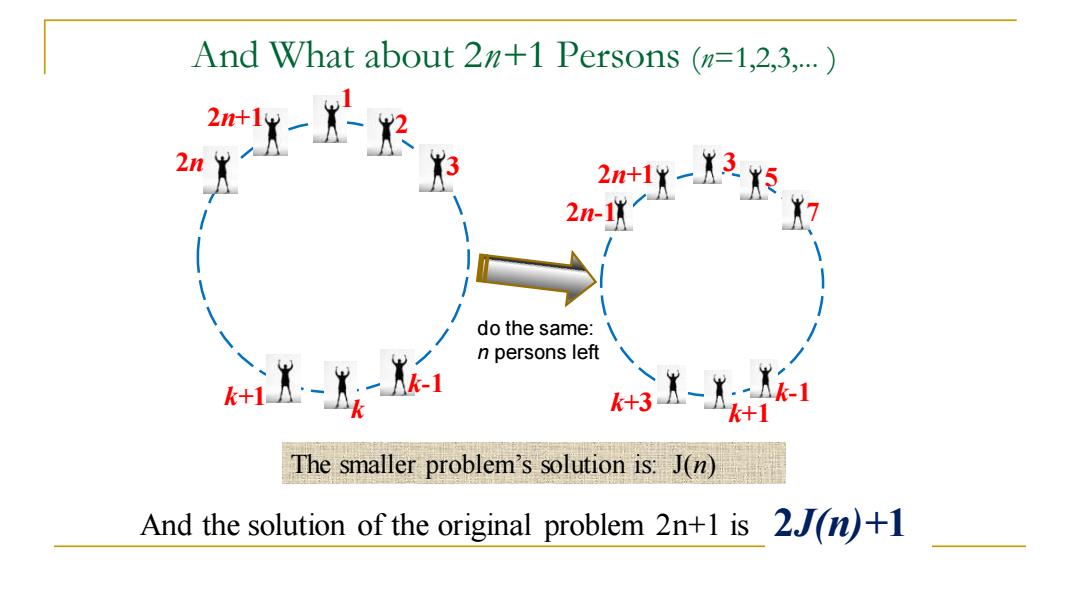
And What about 2n+1 Persons (n=1,2,3,... ) 1 2n+1 2 2n 3 k+1 k k-1 3 2n+1 5 2n-1 7 k+3 k+1 k-1 do the same: n persons left The smaller problem’s solution is: J(n) And the solution of the original problem 2n+1 is ...... 2J(n)+1

递归方程:奇偶数分情况列出 J01)=1; J2m)=2Jn)-1, forn≥1g J2m+1)=2Jm)+1, forn≥1. 间题3 你能解出这个递归式吗? 你能看出什么规律吗? 8 9 10 1112 13 14 15 16 17 J(n) 3 35 3 579 111315 3
递归方程:奇偶数分情况列出 n 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 J(n) 1 1 3 1 3 5 7 1 3 5 7 9 11 13 15 1 3

Eureka! If we write n in the form n=2m+l (where 2m is the largest power of 2 not exceeding n and where is what's left), the solution to our recurrence seems to be: J2m+l)=2L+1,form≥0and0≤l<2m As an example:J(100)=J(64+36)=36*2+1=73 问题48 你能否想出一种简单易行的计算功办法?
Eureka! If we write n in the form n = 2m + l, (where 2m is the largest power of 2 not exceeding n and where l is what's left), the solution to our recurrence seems to be: As an example: J(100) = J(64+36) = 36*2+1 = 73

用二进制表示 Suppose n's binary expansion is n (bmbm-1...b1 bo)2 then:n (1bm-1bm-2...b1 bo)2, L=(0bm-1bm-2.b1bo)2, 2L=(bm-1bm-2.b1bo0)2, 2L+1=(bm-1bm-2..b1bo1)2, J(n)=(bm-1bm-2...bi bobm)2 倒如:100=(1100100)2→(1001001)2=73
用二进制表示 ◼ Suppose n’s binary expansion is : ◼ then: 例如:100 = (1100100)2 → (1001001)2 = 73