
Dijkstra算法正确性
Dijkstra算法 正确性
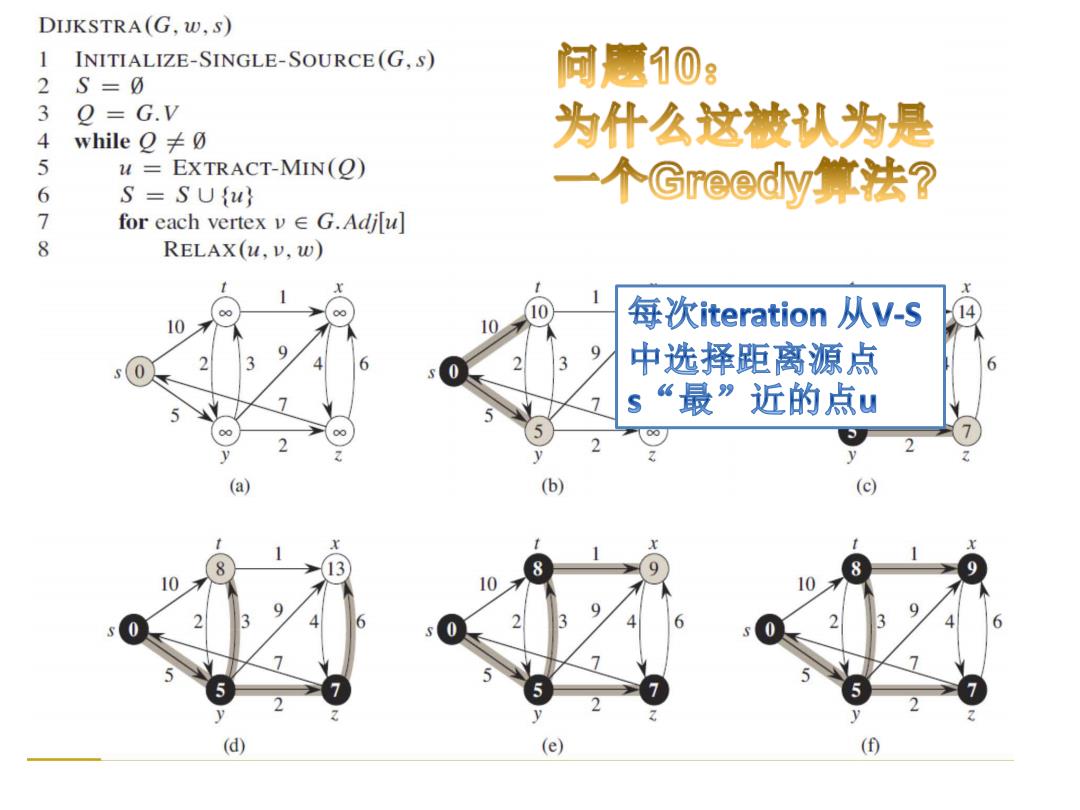
DIJKSTRA(G,w,s) 1 INITIALIZE-SINGLE-SOURCE(G,S) 2 问题1@8 S=0 3 O=G.V 4 while O≠0 为什么这被认为是 5 24= EXTRACT-MIN(O) 6 S=SUfu 一个Greedy.算法? 7 for each vertex v G.Adjlu] 8 RELAX(u,v,w) 10 14 10 10 每次iteration从V-S 9 9 3 3 中选择距离源点 6 “最”近的点u 00 (a) (b) (c) r 8 13 8 9 8 9 10 10 10 9 2 3 6 3 6 5 (d) (e) (f)

DIJKSTRA(G.w.s) 1 INITIALIZE-SINGLE-SOURCE(G.S) 2S=0 3 0=G.V Dijkstra算法正确性 4 while O≠0 5 EXTRACT-MIN(O) 6 S=SUfu 7 for each vertex vE G.Adjlu] 8 RELAX(u.V.w) Corollary 24.7 If we run Dijkstra's algorithm on a weighted,directed graph G =(V,E)with nonnegative weight function w and source s,then at termination,the predecessor subgraph G is a shortest-paths tree rooted at s. predecessor-subgraph property Theorem 24.6 (Correctness of Dijkstra's algorithm) Dijkstra's algorithm,run on a weighted,directed graph G =(V,E)with non- negative weight function w and source s,terminates with u.d =8(s,u)for all vertices u e V
Dijkstra算法 正确性 predecessor-subgraph property

DIJKSTRA(G.w.s) 1 INITIALIZE-SINGLE-SOURCE(G.S) 2 S=0 3 O=G.V Dijkstra算法正确性 4 while O≠g 5 EXTRACT-MIN(O) 6 S=SUfu 7 for each vertex vE G.Adjlu] 8 RELAX(u.V.w) Theorem 24.6(Correctness of Dijkstra's algorithm) Dijkstra's algorithm,run on a weighted,directed graph G=(V,E)with non- negative weight function w and source s,terminates with u.d =8(s,u)for all vertices u e V. Proof We use the following loop invariant: At the start of each iteration of the while loop of lines 4-8,v.d 8(s,v) for each vertex v∈S. It suffices to show for each vertex u E V,we have u.d =8(s.u)at the time when u is added to set S.Once we show that u.d =8(s.u),we rely on the upper-bound property to show that the equality holds at all times thereafter
Dijkstra算法 正确性

DIJKSTRA(G.w.s) 1 INITIALIZE-SINGLE-SOURCE(G.S) 2S=0 3 0=G.V Dijkstra算法正确性 4 while O≠0 5 EXTRACT-MIN(O) 6 S=SUu 7 for each vertex v G.Adjlu] 8 RELAX(.v.w) 初始阶段(Initialization): -S=0,不变式显然成立 0 运行期间(Maintenance): We wish to show that in each iteration,u.d =o(s,d)for the vertex u added to set S. ·终止时刻(Termination) Termination:At termination,=0 which,along with our earlier invariant that O=V-S,implies that S=V.Thus,u.d =8(s,u)for all vertices u V
Dijkstra算法 正确性 • 初始阶段(Initialization): – 𝑆 = ∅, 不变式显然成立 • 运行期间(Maintenance): – We wish to show that in each iteration, 𝒖. 𝒅 = 𝜹(𝒔, 𝒅) for the vertex 𝒖 added to set S. • 终止时刻(Termination)