
Definition of three kinds of charge density Volume density do p= Charge per unit volume dxdydz Area density Charge per unit area d№=pd dxdy Linear density 1= Charge per unit length de =ody=pdyd dx Always used in different dimensionalities according to different symmetries. 6
Volume density Charge per unit volume Area density Charge per unit area Linear density Charge per unit length dxdydz dQ dz dxdy dQ dy dydz dx dQ x y z Always used in different dimensionalities according to different symmetries. Definition of three kinds of charge density 6

Calculation of electric static field Example 1 Calculate the electricfield at above the midpoint ofa straight line segment of length 21. which carries a uniform charge ofQ For a long thin straight wire,although it has three dimensionalities,we can use linear charge density to describe the charge distribution when the scale length we study is much larger than their its transverse size. 40 p= + πd21 九= Q/1 十 E(z) 21 0 Z ++ Discuss: l.l→infinite 2.z>>1 E=E.e.= 1 21 4πE0z√z2+12
For a long thin straight wire, although it has three dimensionalities, we can use linear charge density to describe the charge distribution when the scale length we study is much larger than their its transverse size. d Q l d l Q / 4 2 7 Calculation of electric static field + + + + + + + + + + + + E(z) 2l z q Example 1 Calculate the electric field at z above the midpoint of a straight line segment of length 2l, which carries a uniform charge of Q. z z z e z z l l E E e ˆ 2 4 1 ˆ 2 2 0 e Discuss: 1. l infinite 2. z>>l
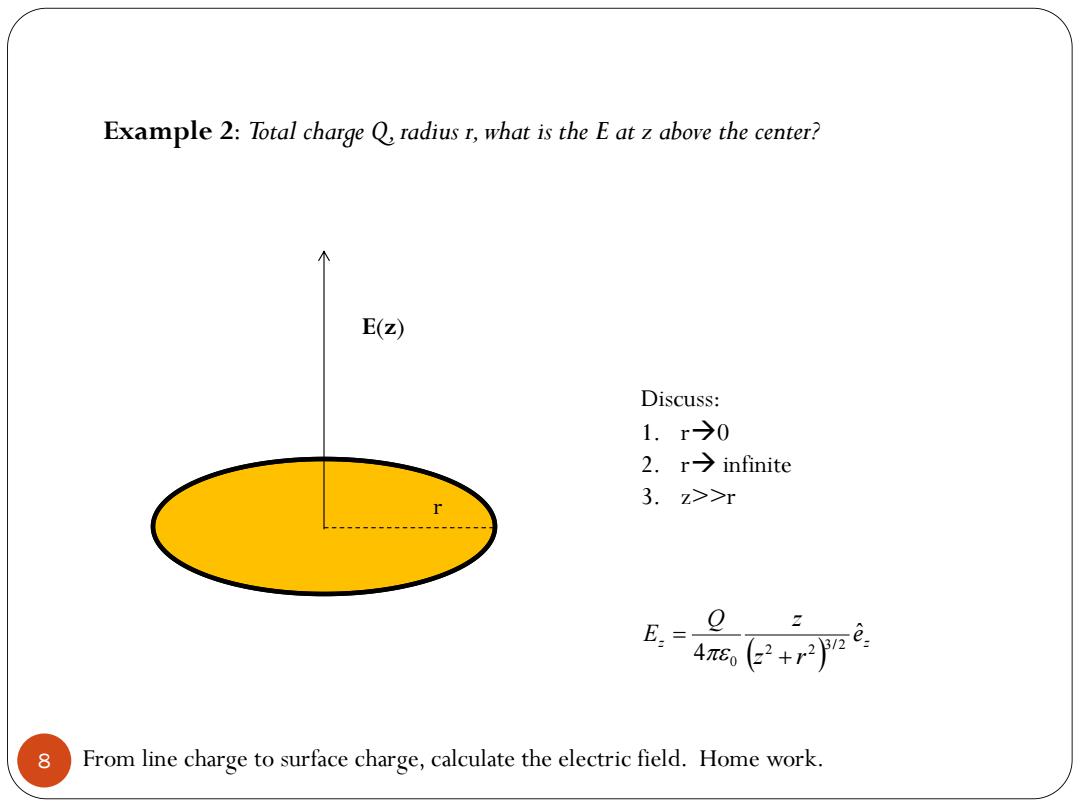
Example 2:Total charge Q radius r,what is the E atz above the center? 个 E(z) Discuss: 1.r→0 2.r→infinite 3.z>>r Q 8 From line charge to surface charge,calculate the electric field.Home work
8 Example 2: Total charge Q,radius r,what is the E at z above the center? r E(z) Discuss: 1. r0 2. r infinite 3. z>>r From line charge to surface charge,calculate the electric field. Home work. z z e z r Q z E ˆ 4 3/ 2 2 2 0 e

Example 3:Infinite Plane Sheet of Charge,surface density of charge. d Divide the plane into slides with width of dx along y direction. dq=oLdx,then the line density is=odx From Ex.1,we know dE=odx/r2To 12l 它=Ee,=460N2+ e. a -c0 o 2 arctan- 三 a 9
9 Example 3: Infinite Plane Sheet of Charge,surface density of charge . Divide the plane into slides with width of dx along y direction. dq= Ldx, then the line density is = dx From Ex.1, we know dE= dx/r2e0 z z z e z z l l E E e ˆ 2 4 1 ˆ 2 2 0 e 0 0 2 2 0 0 2 arctan 1 2 2 sin 2 e e e q e a x a a dx a x a dx r E dEz
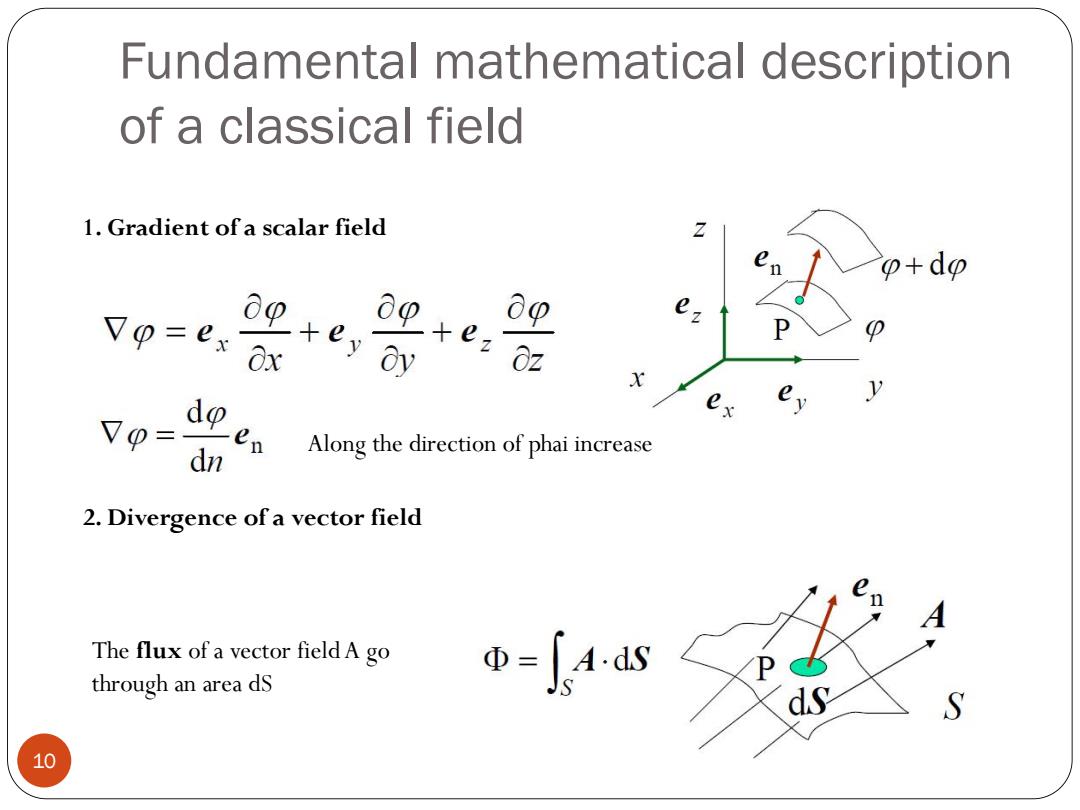
Fundamental mathematical description of a classical field 1.Gradient of a scalar field P+do o⑨+eyy o=ex Ox 09+ez02 00 1 V0二 dn Along the direction of phai increase 2.Divergence of a vector field The flux of a vector field A go through an area dS w-Jas 10
Fundamental mathematical description of a classical field 10 1. Gradient of a scalar field Along the direction of phai increase 2. Divergence of a vector field The flux of a vector fieldA go through an area dS