
第12卷第5期 智能系统学报 Vol.12 No.5 2017年10月 CAAI Transactions on Intelligent Systems 0ct.2017 D0I:10.11992/tis.201703042 网络出版地址:http:/kns.cmki.net/kcms/detail/23.1538.TP.20170702.1547.036.html 具有两类请求的云计算中心服务器数量的优化 张江强,赵宁,刘文奇 (昆明理工大学理学院,云南昆明650500) 摘要:为提高云计算中心的服务质量,节约系统成本,针对具有两类用户请求的云计算中心,提出云计算中心的服 务器数量的优化方案。首先.建立了具有两类用户请求的排队模型,分析系统的稳态概率分布、平均队长等性能指 标:然后,建立了云计算中心的能耗模型:最后,联合系统的等待成本和能耗成本,构建系统的成本函数,对系统的服 务器数量进行优化,从而使系统的成本最小。数值分析结果表明最优服务器数量是用户请求到达率的非减函数,为 了使系统成本最小,云计算中心需要动态调整服务器的数量。 关键词:云计算:排队系统:两类请求:性能指标:能耗:成本:服务器数量的优化 中图分类号:TP393.02文献标志码:A文章编号:1673-4785(2017)05-0601-07 中文引用格式:张江强,赵宁,刘文奇.具有两类请求的云计算中心服务器数量的优化[J].智能系统学报,2017,12(5):601-607. 英文引用格式:ZHANG Jiangqiang,ZHAO Ning,LIU Wengi..Optimization of the number of servers in a cloud computation center with two demand classes[J].CAAI transactions on intelligent systems,2017,12(5):601-607. Optimization of the number of servers in a cloud computation center with two demand classes ZHANG Jiangqiang,ZHAO Ning,LIU Wenqi (Faculty of Science,Kunming University of Science and Technology,Kunming 650500,China) Abstract:In order to improve the service quality and to save the system cost of the cloud computing center,for a cloud computing center with two demand classes,a method to optimize the number of servers was proposed.First,a queuing model having two demand classes was established for analyzing performance measures such as distribution of the probability of stability and mean queue length;next,a power consumption model was established on the cloud computing center;finally,the wait and power-consumption cost of the system were used together to construct the cost function of the system and optimize the server quantity for realizing the lowest cost.The numerical results show that the optimal number of servers is a non-decreasing function of the arrival rate of demands.To minimize the system cost,dynamically adjusting the number of servers is necessary. Keywords:cloud computing;queuing system;two demand classes;performance measure;power consumption; cost;optimization of the number of servers 云计算中心是基于超级计算机系统对外提供 云计算中心作为服务机构,系统的性能指标 计算资源、存储资源等服务的机构或单位,以高性 (用户请求的等待时间、系统的堵塞程度等)是刻画 能计算机为基础面向各界提供高性能计算服务。 服务质量的重要因素。将用户请求看作顾客,云计 当前,云计算中心主要面向大规模科学计算及工程 算中心的超级计算机的处理器作为服务器,而用户 计算应用,并在商业计算、互联网、电子政务、电子 请求的处理过程作为服务过程,云计算中心是一个 商务等领域拥有巨大发展潜力。对云计算中心的 典型的排队系统。很多学者对云计算中心的性能 性能和能耗进行全面地分析具有十分重要的意义。 及调度策略方面展开研究。廖倩文等)提出一种 基于排队论的批量到达的云计算中心性能分析模 收稿日期:2017-03-27.网络出版日期:2017-07-02. 基金项目:国家自然科学基金项目(71501086,61573173). 型,得到系统中用户请求队长的稳态概率分布、系 通信作者:赵宁.E-mail:zhaoning@kmust.cd.cn, 统的阻塞概率、立即服务概率等指标。徐小龙等]
第 12 卷第 5 期 智 能 系 统 学 报 Vol.12 №.5 2017 年 10 月 CAAI Transactions on Intelligent Systems Oct. 2017 DOI:10.11992 / tis.201703042 网络出版地址:http: / / kns.cnki.net / kcms/ detail / 23.1538.TP.20170702.1547.036.html 具有两类请求的云计算中心服务器数量的优化 张江强,赵宁,刘文奇 (昆明理工大学 理学院,云南 昆明 650500) 摘 要:为提高云计算中心的服务质量,节约系统成本,针对具有两类用户请求的云计算中心,提出云计算中心的服 务器数量的优化方案。 首先,建立了具有两类用户请求的排队模型,分析系统的稳态概率分布、平均队长等性能指 标;然后,建立了云计算中心的能耗模型;最后,联合系统的等待成本和能耗成本,构建系统的成本函数, 对系统的服 务器数量进行优化,从而使系统的成本最小。 数值分析结果表明最优服务器数量是用户请求到达率的非减函数,为 了使系统成本最小,云计算中心需要动态调整服务器的数量。 关键词:云计算;排队系统;两类请求;性能指标;能耗;成本;服务器数量的优化 中图分类号:TP393.02 文献标志码:A 文章编号:1673-4785(2017)05-0601-07 中文引用格式:张江强,赵宁,刘文奇.具有两类请求的云计算中心服务器数量的优化[J]. 智能系统学报, 2017, 12(5): 601-607. 英文引用格式:ZHANG Jiangqiang, ZHAO Ning, LIU Wenqi. Optimization of the number of servers in a cloud computation center with two demand classes[J]. CAAI transactions on intelligent systems, 2017, 12(5): 601-607. Optimization of the number of servers in a cloud computation center with two demand classes ZHANG Jiangqiang, ZHAO Ning, LIU Wenqi (Faculty of Science, Kunming University of Science and Technology, Kunming 650500, China) Abstract:In order to improve the service quality and to save the system cost of the cloud computing center, for a cloud computing center with two demand classes, a method to optimize the number of servers was proposed. First, a queuing model having two demand classes was established for analyzing performance measures such as distribution of the probability of stability and mean queue length; next, a power consumption model was established on the cloud computing center; finally, the wait and power⁃consumption cost of the system were used together to construct the cost function of the system and optimize the server quantity for realizing the lowest cost. The numerical results show that the optimal number of servers is a non⁃decreasing function of the arrival rate of demands. To minimize the system cost, dynamically adjusting the number of servers is necessary. Keywords:cloud computing; queuing system; two demand classes; performance measure; power consumption; cost; optimization of the number of servers 收稿日期:2017-03-27. 网络出版日期:2017-07-02. 基金项目:国家自然科学基金项目(71501086,61573173). 通信作者:赵宁. E⁃mail:zhaoning@ kmust.edu.cn. 云计算中心是基于超级计算机系统对外提供 计算资源、存储资源等服务的机构或单位,以高性 能计算机为基础面向各界提供高性能计算服务。 当前,云计算中心主要面向大规模科学计算及工程 计算应用,并在商业计算、互联网、电子政务、电子 商务等领域拥有巨大发展潜力。 对云计算中心的 性能和能耗进行全面地分析具有十分重要的意义。 云计算中心作为服务机构,系统的性能指标 (用户请求的等待时间、系统的堵塞程度等)是刻画 服务质量的重要因素。 将用户请求看作顾客,云计 算中心的超级计算机的处理器作为服务器,而用户 请求的处理过程作为服务过程,云计算中心是一个 典型的排队系统。 很多学者对云计算中心的性能 及调度策略方面展开研究。 廖倩文等[1] 提出一种 基于排队论的批量到达的云计算中心性能分析模 型,得到系统中用户请求队长的稳态概率分布、系 统的阻塞概率、立即服务概率等指标。 徐小龙等[2]

·602. 智能系统学报 第12卷 研究了云计算系统任务调度和数据部署层面的节 统的性能和能耗构建系统的成本函数,对系统处理 能机制,提出一种面向绿色云计算中心的动态数据 器的个数进行优化。 聚集算法。许丞[3)建议将Hadoop云平台的任务监 1 控和任务调度管理功能分离,从而提升云平台的工 系统描述 作效率。倪志伟)综合考虑了用户最短等待时间 假设云计算中心有c个平行的服务器,按照用 资源负载均衡和经济原则,提出一种离散人工蜂群 户的优先级别,将用户请求分为两类,第i类用户请 算法的云任务调度优化策略。 求到达过程是参数为入,的泊松过程,i=1,2。系统 在云计算中心,能耗开销是不容忽视的问题, 最多容纳N个用户请求,当系统中的用户请求个数 著名T企业如Google、Microsoft、Amazon等云计算 小于N,用户请求的到达率为入=入,+入2,否则到达 中心每年能耗超过百万美元,给云计算中心长期运 率入=0。用户请求到达云计算中心后,如果系统中 营带来了巨大经济负担。云计算中心的能耗问题 有空闲的服务器,则用户请求直接进入空闲服务器 最近得到学者的广泛关注。罗亮等[)从处理器性 接受服务,反之则需要在缓冲区中排队等待接受服 能计数器和系统使用情况入手,结合多元线性回归 务。第1类用户请求相对第2类用户请求具有非抢 和非线性回归的数学方法,分析不同参数和方法对 占优先权,即系统中的第1类用户请求被优先服务, 服务器能耗建模的影响,并提出适合云计算中心基 但是第1类用户请求不能打断第2类用户请求的服 础架构的服务器能耗模型。现有内存能耗模型研 务,对于每1类用户请求,系统按照先到先服务的规 究发现,影响内存能耗的主要因素是内存读写的吞 则(FCFS)进行服务。第i类用户请求的服务时间 吐量[6)。何怀文等)]在平均响应时间受限的条件 服从参数为4:的指数分布,i=1,2。 下提出云计算中心异构服务器之间的优化能耗分 2 配方法。针对云计算中心由于服务器空闲而产生 系统性能分析 大量空闲能耗,以及由于任务调度不匹配而产生大 具有两类用户请求的云计算中心是一个非抢 量“奢侈”能耗的问题,文献[8-10]提出通过任务调 占优先权的M1,M2/M,M2/(c/N)排队模型,如图 度的方式优化管理。文献[11]研究了云计算中心 1所示。 的动态迁移问题。文献[12]以利润最大化为目标, 分析了云计算中心的优化配置。针对多个服务器 用 第1类用户请求 切换过程存在大量冗余信号的问题,文献[13]提出 缓冲区 用户请求 了一种改进的多业务切换机制。文献[14]运用遗 到 达 第2类用户 c- 传算法分析用户请求的调度策略,从而提高云计算 请求 c】 中心能源利用率。文献[15-16]对云计算中心的能 耗和性能进行了联合优化。 图1具有两类用户请求的排队系统 以上关于云计算中心的相关研究都假设系统 Fig.1 Queueing system with two demand classes 只有一类用户请求,但实际应用中,云计算中心根 据用户请求的重要程度分为不同等级[]。例如,云 令(L1,2)表示系统的状态,其中(表示系统中 计算中心将实时用户请求赋予高优先权,将非实时 第i类用户请求的个数,该系统的状态空间为 用户请求赋予低优先权。另外,为了吸引更多客 E={(l1,l2),L1,l2=0,1,…,V,l1+l2=N}。 户,云计算中心为用户提供免费体验的服务,而付 费的用户相对免费用户享有高优先权。Lu等[1]运 系统被第i类用户请求占用系统的概率为P:= cμ 用博弈论的方法研究具有多类用户请求的云计算 (i=1,2),令p=P1+P2。当p<1时,该系统存在稳 中心的预约服务策略。 态概率分布。令1=l,+2为系统的水平(即系统中 本文将研究具有两类用户请求的云计算中心 请求总数),对系统的状态按照水平划分,并且每个 能耗和性能的联合优化问题。假设两类用户请求 水平下的状态按照如下规则排序。 的到达过程均为泊松过程,系统有多个平行的处理 l=0的状态:(0,0)。 器,每个用户请求的处理时间服从指数分布,系统 l=1的状态:(1,0),(0,1)。 最多容纳有限的用户请求。我们将该系统构建为 1=2的状态:(2,0),(1,1),(0,2)。 ,个带非抢占优先权的马尔可夫过程,基于排队论 对该系统的性能进行分析。将系统的能耗表示为 l=N的状态:(N,0),(N-1,1),(N-2,2),, 处理器吞吐量和处理器个数的函数。最后,结合系 (2,N-2),(1,N-1),(0,N)
研究了云计算系统任务调度和数据部署层面的节 能机制, 提出一种面向绿色云计算中心的动态数据 聚集算法。 许丞[3]建议将 Hadoop 云平台的任务监 控和任务调度管理功能分离,从而提升云平台的工 作效率。 倪志伟[4] 综合考虑了用户最短等待时间 资源负载均衡和经济原则,提出一种离散人工蜂群 算法的云任务调度优化策略。 在云计算中心,能耗开销是不容忽视的问题, 著名 IT 企业如 Google、Microsoft、 Amazon 等云计算 中心每年能耗超过百万美元,给云计算中心长期运 营带来了巨大经济负担。 云计算中心的能耗问题 最近得到学者的广泛关注。 罗亮等[5] 从处理器性 能计数器和系统使用情况入手,结合多元线性回归 和非线性回归的数学方法,分析不同参数和方法对 服务器能耗建模的影响,并提出适合云计算中心基 础架构的服务器能耗模型。 现有内存能耗模型研 究发现,影响内存能耗的主要因素是内存读写的吞 吐量[6] 。 何怀文等[7] 在平均响应时间受限的条件 下提出云计算中心异构服务器之间的优化能耗分 配方法。 针对云计算中心由于服务器空闲而产生 大量空闲能耗,以及由于任务调度不匹配而产生大 量“奢侈”能耗的问题,文献[8-10]提出通过任务调 度的方式优化管理。 文献[11] 研究了云计算中心 的动态迁移问题。 文献[12]以利润最大化为目标, 分析了云计算中心的优化配置。 针对多个服务器 切换过程存在大量冗余信号的问题,文献[13]提出 了一种改进的多业务切换机制。 文献[14] 运用遗 传算法分析用户请求的调度策略,从而提高云计算 中心能源利用率。 文献[15-16]对云计算中心的能 耗和性能进行了联合优化。 以上关于云计算中心的相关研究都假设系统 只有一类用户请求,但实际应用中,云计算中心根 据用户请求的重要程度分为不同等级[17] 。 例如,云 计算中心将实时用户请求赋予高优先权,将非实时 用户请求赋予低优先权。 另外,为了吸引更多客 户,云计算中心为用户提供免费体验的服务,而付 费的用户相对免费用户享有高优先权。 Liu 等[18]运 用博弈论的方法研究具有多类用户请求的云计算 中心的预约服务策略。 本文将研究具有两类用户请求的云计算中心 能耗和性能的联合优化问题。 假设两类用户请求 的到达过程均为泊松过程,系统有多个平行的处理 器,每个用户请求的处理时间服从指数分布,系统 最多容纳有限的用户请求。 我们将该系统构建为 一个带非抢占优先权的马尔可夫过程,基于排队论 对该系统的性能进行分析。 将系统的能耗表示为 处理器吞吐量和处理器个数的函数。 最后,结合系 统的性能和能耗构建系统的成本函数,对系统处理 器的个数进行优化。 1 系统描述 假设云计算中心有 c 个平行的服务器,按照用 户的优先级别,将用户请求分为两类,第 i 类用户请 求到达过程是参数为 λi 的泊松过程, i = 1,2。 系统 最多容纳 N 个用户请求,当系统中的用户请求个数 小于 N ,用户请求的到达率为 λ = λ1 + λ2 ,否则到达 率 λ = 0。 用户请求到达云计算中心后,如果系统中 有空闲的服务器,则用户请求直接进入空闲服务器 接受服务,反之则需要在缓冲区中排队等待接受服 务。 第 1 类用户请求相对第 2 类用户请求具有非抢 占优先权,即系统中的第 1 类用户请求被优先服务, 但是第 1 类用户请求不能打断第 2 类用户请求的服 务,对于每 1 类用户请求,系统按照先到先服务的规 则(FCFS)进行服务。 第 i 类用户请求的服务时间 服从参数为 μi 的指数分布,i = 1,2。 2 系统性能分析 具有两类用户请求的云计算中心是一个非抢 占优先权的 M1 ,M2 / M1 ,M2 / (c/ N) 排队模型,如图 1 所示。 图 1 具有两类用户请求的排队系统 Fig.1 Queueing system with two demand classes 令(l 1 ,l 2 )表示系统的状态,其中 l i 表示系统中 第 i 类用户请求的个数,该系统的状态空间为 E = l 1 ,l 2 ( ) ,l 1 ,l 2 = 0,1,…,N,l 1 + l 2 { = N} 。 系统被第 i 类用户请求占用系统的概率为 ρi = λi cμi , (i = 1,2), 令 ρ = ρ1 + ρ2 。 当ρ < 1时,该系统存在稳 态概率分布。 令 l = l 1 + l 2 为系统的水平(即系统中 请求总数),对系统的状态按照水平划分,并且每个 水平下的状态按照如下规则排序。 l = 0 的状态: (0,0) 。 l = 1 的状态: (1,0) ,(0,1) 。 l = 2 的状态: (2,0), (1,1), (0,2)。 ︙ l = N 的状态:(N,0),(N-1,1),(N-2,2),…, (2,N-2),(1,N-1),(0,N)。 ·602· 智 能 系 统 学 报 第 12 卷
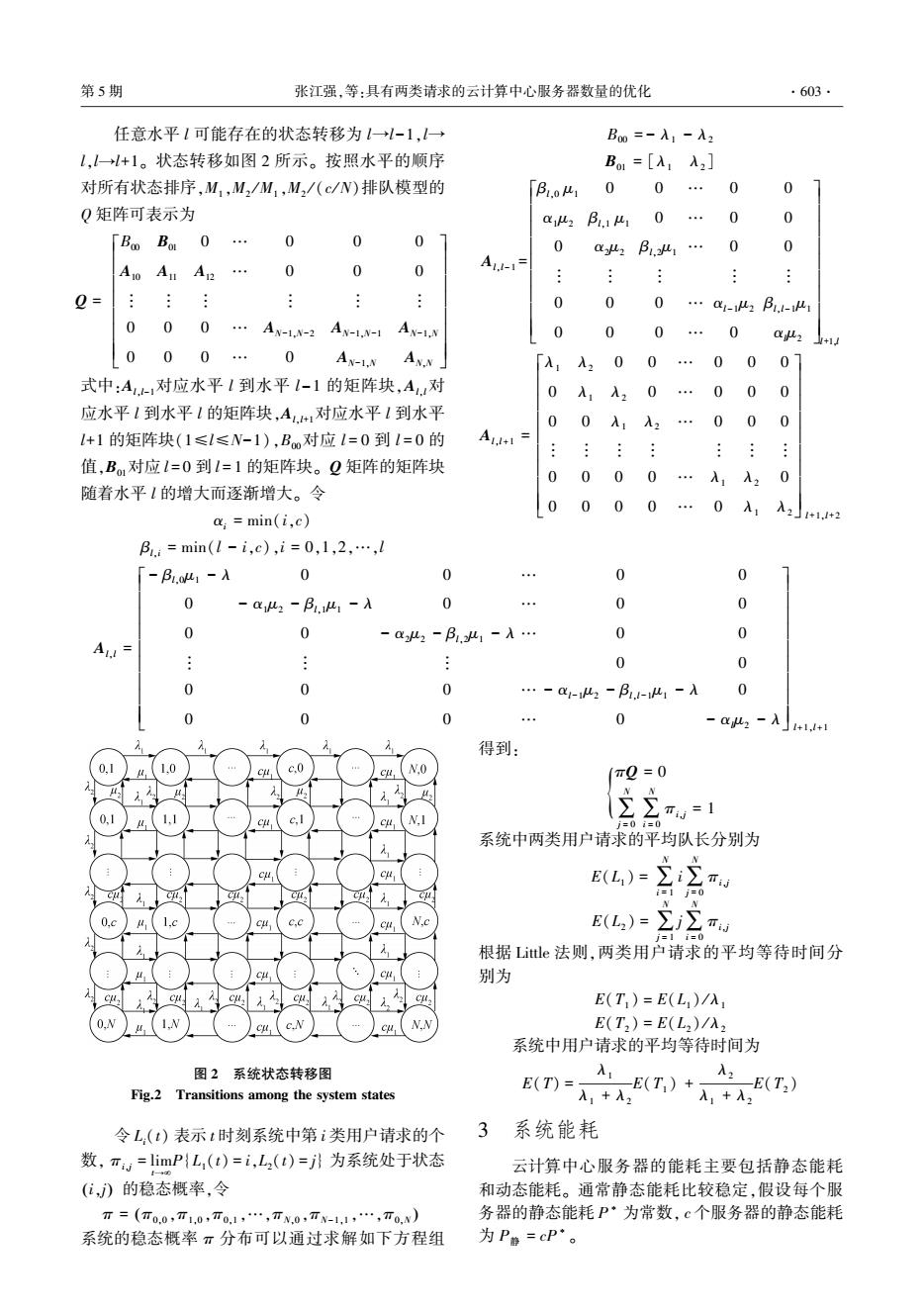
第5期 张江强,等:具有两类请求的云计算中心服务器数量的优化 ·603 任意水平1可能存在的状态转移为1→l-1,【一→ B0=-入1-入2 1,→+1。状态转移如图2所示。按照水平的顺序 Bo1=[A1入2] 对所有状态排序,M,M,/M1,M2/(c/N)排队模型的 B.01 00 0 0 0矩阵可表示为 a Bi. 0 0 0 Bo Bot 0… 0 0 0 42B.业1… 0 0 A10 Au A 0 0 0 A1.-1= 0= 0 0 0 …a1-2B,-1 0 0 0…A-1,N-2A-1-1A-1,N 0 0 0 0 2 +1 000… 0 AN-1N AxN」 「入1入200… 0007 式中:A.对应水平1到水平1-1的矩阵块,A,u对 0入1入2 0 0 0 0 应水平l到水平l的矩阵块,A,1对应水平l到水平 0 0入 入, 0 0 0 l+1的矩阵块(1≤l≤N-1),Bo对应l=0到l=0的 A1,+1= 值,B1对应l=0到l=1的矩阵块。Q矩阵的矩阵块 0 00 0 入1入2 0 随着水平(的增大而逐渐增大。令 0 00 0 0 入2 a;min(i,c) 1+1.1+2 B.:=min(l-i,c),i=0,1,2,…,l 「-B.1-入0 0 0 0 0 -C2-B.41-入 0 0 0 0 0 -a2-β,1-入… 0 0 A,= 0 0 0 0 0 …-a-2-B-41-入 0 0 0 0 得到: 1.0 c.0 N.0 (πQ=0 C N.I πw=1 系统中两类用户请求的平均队长分别为 N E(L,)= cu, =1j=0 N 09 c.c E(L2)= im. i=1i=0 根据Little法则,两类用户请求的平均等待时间分 C 别为 cu E(T)=E(L)/入 c E(T2)=E(L2)/入2 系统中用户请求的平均等待时间为 图2系统状态转移图 Fig.2 Transitions among the system states E(T)= 入一E(T)+ 入1+入2 ,一E(T) 入,+入, 令L,(t)表示t时刻系统中第i类用户请求的个 3 系统能耗 数,πw=limP{L,(t)=i,L,()=j}为系统处于状态 云计算中心服务器的能耗主要包括静态能耗 (i,)的稳态概率,令 和动态能耗。通常静态能耗比较稳定,假设每个服 T=(T0.0,T10,T0.1,,TN,0,TN-1,1,…,T0,N) 务器的静态能耗P·为常数,c个服务器的静态能耗 系统的稳态概率π分布可以通过求解如下方程组 为P静=cP·
任意水平 l 可能存在的状态转移为 l→l-1,l→ l,l→l+1。 状态转移如图 2 所示。 按照水平的顺序 对所有状态排序,M1 ,M2 / M1 ,M2 / (c/ N)排队模型的 Q 矩阵可表示为 Q = B00 B01 0 … 0 0 0 A10 A11 A12 … 0 0 0 ︙ ︙ ︙ ︙ ︙ ︙ 0 0 0 … AN-1,N-2 AN-1,N-1 AN-1,N 0 0 0 … 0 AN-1,N AN,N é ë ê ê ê ê ê ê êê ù û ú ú ú ú ú ú úú 式中:Al,l-1对应水平 l 到水平 l-1 的矩阵块,Al,l对 应水平 l 到水平 l 的矩阵块,Al,l+1对应水平 l 到水平 l+1 的矩阵块(1≤l≤N-1),B00对应 l = 0 到 l = 0 的 值,B01对应 l = 0 到 l = 1 的矩阵块。 Q 矩阵的矩阵块 随着水平 l 的增大而逐渐增大。 令 αi = min(i,c) βl,i = min(l - i,c),i = 0,1,2,…,l B00 = - λ1 - λ2 B01 = [λ1 λ2 ] Al,l-1 = βl,0 μ1 0 0 … 0 0 α1μ2 βl,1 μ1 0 … 0 0 0 α2μ2 βl,2μ1 … 0 0 ︙ ︙ ︙ ︙ ︙ 0 0 0 … αl-1μ2 βl,l-1μ1 0 0 0 … 0 αlμ2 é ë ê ê ê ê ê ê ê ê ê ù û ú ú ú ú ú ú ú ú ú l+1,l Al,l+1 = λ1 λ2 0 0 … 0 0 0 0 λ1 λ2 0 … 0 0 0 0 0 λ1 λ2 … 0 0 0 ︙ ︙ ︙ ︙ ︙ ︙ ︙ 0 0 0 0 … λ1 λ2 0 0 0 0 0 … 0 λ1 λ2 é ë ê ê ê ê ê ê ê ê ê ù û ú ú ú ú ú ú ú ú ú l+1,l+2 Al,l = - βl,0μ1 - λ 0 0 … 0 0 0 - α1μ2 - βl,1μ1 - λ 0 … 0 0 0 0 - α2μ2 - βl,2μ1 - λ … 0 0 ︙ ︙ ︙ 0 0 0 0 0 … - αl-1μ2 - βl,l-1μ1 - λ 0 0 0 0 … 0 - αlμ2 - λ é ë ê ê ê ê ê ê ê ê ê ù û ú ú ú ú ú ú ú ú ú l+1,l+1 图 2 系统状态转移图 Fig.2 Transitions among the system states 令 Li(t) 表示 t 时刻系统中第 i 类用户请求的个 数, πi,j = lim t→¥ P{L1(t) = i,L2(t) = j} 为系统处于状态 (i,j) 的稳态概率,令 π = π0,0 ,π1,0 ,π0,1 ,…,πN,0 ,πN-1,1 ,…,π0,N ( ) 系统的稳态概率 π 分布可以通过求解如下方程组 得到: πQ = 0 ∑ N j = 0 ∑ N i = 0 πi,j { = 1 系统中两类用户请求的平均队长分别为 E(L1 ) = ∑ N i = 1 i∑ N j = 0 πi,j E(L2 ) = ∑ N j = 1 j∑ N i = 0 πi,j 根据 Little 法则,两类用户请求的平均等待时间分 别为 E(T1 ) = E(L1 ) / λ1 E(T2 ) = E(L2 ) / λ2 系统中用户请求的平均等待时间为 E(T) = λ1 λ1 + λ2 E(T1 ) + λ2 λ1 + λ2 E(T2 ) 3 系统能耗 云计算中心服务器的能耗主要包括静态能耗 和动态能耗。 通常静态能耗比较稳定,假设每个服 务器的静态能耗 P ∗ 为常数, c 个服务器的静态能耗 为 P静 = cP ∗ 。 第 5 期 张江强,等:具有两类请求的云计算中心服务器数量的优化 ·603·
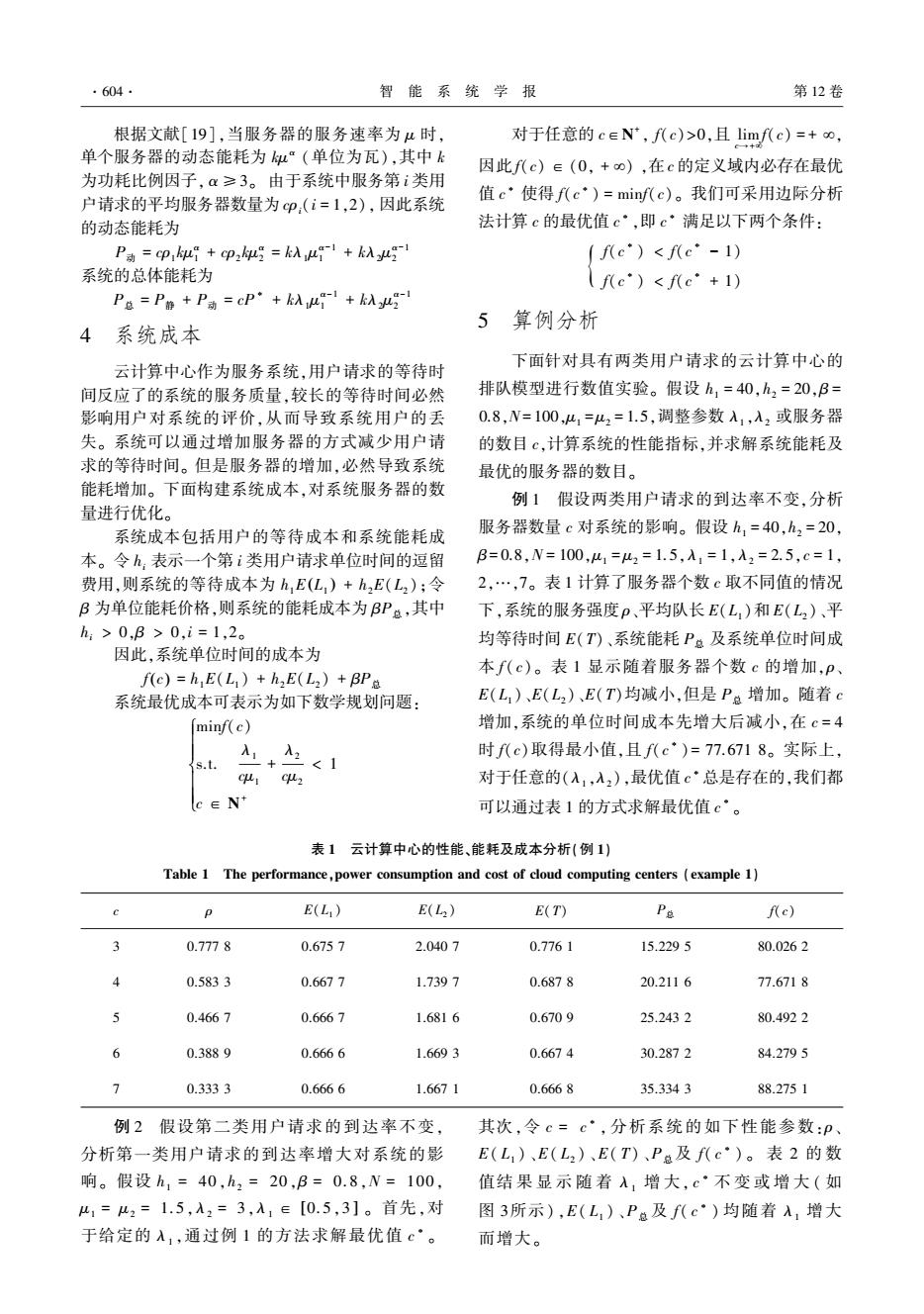
·604. 智能系统学报 第12卷 根据文献[19],当服务器的服务速率为时, 对于任意的ceN,fc)>0,且limf(c)=+o, 单个服务器的动态能耗为似(单位为瓦),其中k 因此f代c)∈(0,+o),在c的定义域内必存在最优 为功耗比例因子,α≥3。由于系统中服务第i类用 户请求的平均服务器数量为cp,(i=1,2),因此系统 值c·使得f(c·)=minf(c)。我们可采用边际分析 的动态能耗为 法计算c的最优值c·,即c·满足以下两个条件: P动=cp1b+p2好=k入u1+k入g- fc)<fc·-1) 系统的总体能耗为 fc)<fc·+1) P=P静+P动=cP·+k入-1+k入- 5 算例分析 4 系统成本 下面针对具有两类用户请求的云计算中心的 云计算中心作为服务系统,用户请求的等待时 间反应了的系统的服务质量,较长的等待时间必然 排队模型进行数值实验。假设h,=40,h2=20,B= 影响用户对系统的评价,从而导致系统用户的 0.8,N=100,41=2=1.5,调整参数入1,A2或服务器 失。系统可以通过增加服务器的方式减少用户请 的数目c,计算系统的性能指标,并求解系统能耗及 求的等待时间。但是服务器的增加,必然导致系统 最优的服务器的数目。 能耗增加。下面构建系统成本,对系统服务器的数 例1假设两类用户请求的到达率不变,分析 量进行优化。 系统成本包括用户的等待成本和系统能耗成 服务器数量c对系统的影响。假设h,=40,h2=20, 本。令h,表示一个第i类用户请求单位时间的逗留 B=0.8,N=100,41=2=1.5,A1=1,A2=2.5,c=1, 费用,则系统的等待成本为h,E(L,)+hE(L,);令 2,…,7。表1计算了服务器个数c取不同值的情况 B为单位能耗价格,则系统的能耗成本为BP。,其中 下,系统的服务强度p、平均队长E(L,)和E(L2)、平 h>0,B>0,i=1,2。 均等待时间E(T)、系统能耗P总及系统单位时间成 因此,系统单位时间的成本为 本f(c)。表1显示随着服务器个数c的增加,p、 f(c)=h;E(L)+h2E(L2)+BP 系统最优成本可表示为如下数学规划问题: E(L,)、E(L2)、E(T)均减小,但是P。增加。随着c minf(c) 增加,系统的单位时间成本先增大后减小,在c=4 入1 A2 时f(c)取得最小值,且f(c°)=77.6718。实际上, s.t. <1 12 对于任意的(入,入2),最优值c·总是存在的,我们都 (c∈Nt 可以通过表1的方式求解最优值c”。 表1云计算中心的性能、能耗及成本分析(例1) Table 1 The performance,power consumption and cost of cloud computing centers (example 1) E(L,) E(L2) E(T) P总 f(c) 3 0.7778 0.6757 2.0407 0.7761 15.2295 80.0262 0.5833 0.6677 1.7397 0.6878 20.2116 77.6718 0.4667 0.6667 1.6816 0.6709 25.2432 80.4922 6 0.3889 0.6666 1.6693 0.6674 30.2872 84.2795 7 0.3333 0.6666 1.6671 0.6668 35.3343 88.2751 例2假设第二类用户请求的到达率不变, 其次,令c=c·,分析系统的如下性能参数:p、 分析第一类用户请求的到达率增大对系统的影 E(L,)、E(L,)、E(T)、Pa及f(c·)。表2的数 响。假设h1=40,h2=20,B=0.8,N=100, 值结果显示随着入,增大,c·不变或增大(如 u1=u2=1.5,入2=3,入1∈[0.5,3]。首先,对 图3所示),E(L,)、P及f(c·)均随着入1增大 于给定的入,通过例1的方法求解最优值c·。 而增大
根据文献[19],当服务器的服务速率为 μ 时, 单个服务器的动态能耗为 kμ α (单位为瓦),其中 k 为功耗比例因子, α ≥3。 由于系统中服务第 i 类用 户请求的平均服务器数量为 cρi(i = 1,2), 因此系统 的动态能耗为 P动 = cρ1 kμ α 1 + cρ2 kμ α 2 = kλ1μ α-1 1 + kλ2μ α-1 2 系统的总体能耗为 P总 = P静 + P动 = cP ∗ + kλ1μ α-1 1 + kλ2μ α-1 2 4 系统成本 云计算中心作为服务系统,用户请求的等待时 间反应了的系统的服务质量,较长的等待时间必然 影响用户对系统的评价,从而导致系统用户的丢 失。 系统可以通过增加服务器的方式减少用户请 求的等待时间。 但是服务器的增加,必然导致系统 能耗增加。 下面构建系统成本,对系统服务器的数 量进行优化。 系统成本包括用户的等待成本和系统能耗成 本。 令 hi 表示一个第 i 类用户请求单位时间的逗留 费用,则系统的等待成本为 h1E L1 ( ) + h2E(L2 );令 β 为单位能耗价格,则系统的能耗成本为 βP总,其中 hi > 0,β > 0,i = 1,2。 因此,系统单位时间的成本为 f(c) = h1E(L1 ) + h2E(L2 ) + βP总 系统最优成本可表示为如下数学规划问题: minf(c) s.t. λ1 cμ1 + λ2 cμ2 < 1 c ∈ N + ì î í ï ïï ï ï 对于任意的 c∈N + , f(c)>0,且 lim c→+¥ f(c) = + ¥, 因此 f(c) ∈ (0, + ¥) ,在 c 的定义域内必存在最优 值 c ∗ 使得 f(c ∗ ) = minf(c)。 我们可采用边际分析 法计算 c 的最优值 c ∗ ,即 c ∗ 满足以下两个条件: f(c ∗ ) < f(c ∗ - 1) f(c ∗ ) < f(c ∗ + 1) { 5 算例分析 下面针对具有两类用户请求的云计算中心的 排队模型进行数值实验。 假设 h1 = 40,h2 = 20,β = 0.8,N= 100,μ1 = μ2 = 1.5,调整参数 λ1 ,λ2 或服务器 的数目 c,计算系统的性能指标,并求解系统能耗及 最优的服务器的数目。 例 1 假设两类用户请求的到达率不变,分析 服务器数量 c 对系统的影响。 假设 h1 = 40,h2 = 20, β = 0.8,N = 100,μ1 = μ2 = 1.5,λ1 = 1,λ2 = 2.5,c = 1, 2,…,7。 表 1 计算了服务器个数 c 取不同值的情况 下,系统的服务强度 ρ、平均队长 E(L1 )和 E(L2 )、平 均等待时间 E(T)、系统能耗 P总 及系统单位时间成 本 f( c)。 表 1 显示随着服务器个数 c 的增加,ρ、 E(L1 )、E(L2 )、E(T)均减小,但是 P总 增加。 随着 c 增加,系统的单位时间成本先增大后减小,在 c = 4 时 f(c)取得最小值,且 f(c ∗ )= 77.671 8。 实际上, 对于任意的(λ1 ,λ2 ),最优值 c ∗总是存在的,我们都 可以通过表 1 的方式求解最优值 c ∗ 。 表 1 云计算中心的性能、能耗及成本分析(例 1) Table 1 The performance,power consumption and cost of cloud computing centers (example 1) c ρ E(L1 ) E(L2 ) E(T) P总 f(c) 3 0.777 8 0.675 7 2.040 7 0.776 1 15.229 5 80.026 2 4 0.583 3 0.667 7 1.739 7 0.687 8 20.211 6 77.671 8 5 0.466 7 0.666 7 1.681 6 0.670 9 25.243 2 80.492 2 6 0.388 9 0.666 6 1.669 3 0.667 4 30.287 2 84.279 5 7 0.333 3 0.666 6 1.667 1 0.666 8 35.334 3 88.275 1 例 2 假设第二类用户请求的到达率不变, 分析第一类用户请求的到达率增大对系统的影 响。 假设 h1 = 40,h2 = 20,β = 0.8,N = 100, μ1 = μ2 = 1.5,λ2 = 3,λ1 ∈ [0.5,3 ] 。 首先,对 于给定的 λ1 ,通过例 1 的方法求解最优值 c ∗ 。 其次,令 c = c ∗ , 分析系统的如下性能参数:ρ、 E( L1 ) 、E( L2 ) 、E( T) 、P 总 及 f( c ∗ ) 。 表 2 的 数 值结 果 显 示 随 着 λ1 增 大, c ∗ 不 变 或 增 大 ( 如 图 3所示) ,E( L1 ) 、P 总 及 f( c ∗ ) 均随着 λ1 增大 而增大。 ·604· 智 能 系 统 学 报 第 12 卷
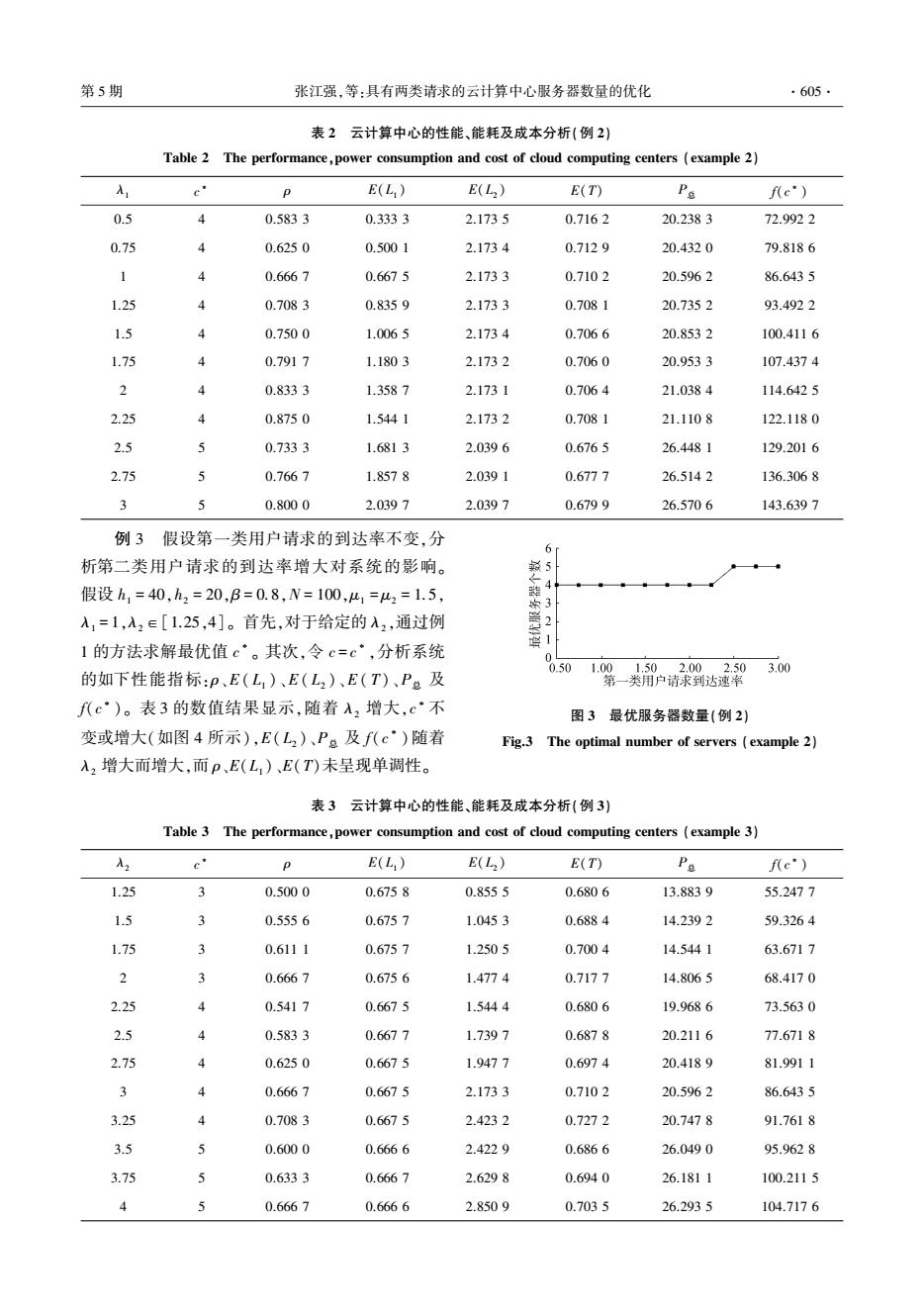
第5期 张江强,等:具有两类请求的云计算中心服务器数量的优化 ·605· 表2云计算中心的性能、能耗及成本分析(例2) Table 2 The performance,power consumption and cost of cloud computing centers(example 2) c" P E(L,) E(L2) E(T) P色 f(e") 0.5 0.5833 0.3333 2.1735 0.7162 20.2383 72.9922 0.75 0.6250 0.5001 2.1734 0.7129 20.4320 79.8186 1 4 0.6667 0.6675 2.1733 0.7102 20.5962 86.6435 1.25 4 0.7083 0.8359 2.1733 0.7081 20.7352 93.4922 1.5 0.7500 1.0065 2.1734 0.7066 20.8532 100.4116 1.75 0.7917 1.1803 2.1732 0.7060 20.9533 107.4374 2 4 0.8333 1.3587 2.1731 0.7064 21.0384 114.6425 2.25 4 0.8750 1.5441 2.1732 0.7081 21.1108 122.1180 2.5 0.7333 1.6813 2.0396 0.6765 26.4481 129.2016 2.75 0.7667 1.8578 2.0391 0.6777 26.5142 136.3068 3 0.8000 2.0397 2.0397 0.6799 26.5706 143.6397 例3假设第一类用户请求的到达率不变,分 6 析第二类用户请求的到达率增大对系统的影响。 假设h1=40,h2=20,B=0.8,N=100,41=u2=1.5, 4 入1=1,入2∈[1.25,4]。首先,对于给定的入2,通过例 1的方法求解最优值c·。其次,令c=c·,分析系统 0 0.50 1.001.502.002.503.00 的如下性能指标:P、E(L,)、E(L2)、E(T)、P总及 第一类用户请求到达速率 f八c)。表3的数值结果显示,随着入2增大,c·不 图3最优服务器数量(例2) 变或增大(如图4所示),E(L2)、P。及f(c°)随着 Fig.3 The optimal number of servers (example 2) 入2增大而增大,而p、E(L,)、E(T)未呈现单调性。 表3云计算中心的性能、能耗及成本分析(例3) Table 3 The performance,power consumption and cost of cloud computing centers example 3) E(L,) E(L2) E(T) P每 f(c) 1.25 2 0.5000 0.6758 0.8555 0.6806 13.8839 55.2477 1.5 3 0.5556 0.6757 1.0453 0.6884 14.2392 59.3264 1.75 0.6111 0.6757 1.2505 0.7004 14.5441 63.6717 2 3 0.6667 0.6756 1.4774 0.7177 14.8065 68.4170 2.25 4 0.5417 0.6675 1.5444 0.6806 19.9686 73.5630 2.5 0.5833 0.6677 1.7397 0.6878 20.2116 77.6718 2.75 0.6250 0.6675 1.9477 0.6974 20.4189 81.9911 3 4 0.6667 0.6675 2.1733 0.7102 20.5962 86.6435 3.25 4 0.7083 0.6675 2.4232 0.7272 20.7478 91.7618 3.5 5 0.6000 0.6666 2.4229 0.6866 26.0490 95.9628 3.75 0.6333 0.6667 2.6298 0.6940 26.1811 100.2115 4 5 0.6667 0.6666 2.8509 0.7035 26.2935 104.7176
表 2 云计算中心的性能、能耗及成本分析(例 2) Table 2 The performance,power consumption and cost of cloud computing centers (example 2) λ1 c ∗ ρ E(L1 ) E(L2 ) E(T) P总 f(c ∗ ) 0.5 4 0.583 3 0.333 3 2.173 5 0.716 2 20.238 3 72.992 2 0.75 4 0.625 0 0.500 1 2.173 4 0.712 9 20.432 0 79.818 6 1 4 0.666 7 0.667 5 2.173 3 0.710 2 20.596 2 86.643 5 1.25 4 0.708 3 0.835 9 2.173 3 0.708 1 20.735 2 93.492 2 1.5 4 0.750 0 1.006 5 2.173 4 0.706 6 20.853 2 100.411 6 1.75 4 0.791 7 1.180 3 2.173 2 0.706 0 20.953 3 107.437 4 2 4 0.833 3 1.358 7 2.173 1 0.706 4 21.038 4 114.642 5 2.25 4 0.875 0 1.544 1 2.173 2 0.708 1 21.110 8 122.118 0 2.5 5 0.733 3 1.681 3 2.039 6 0.676 5 26.448 1 129.201 6 2.75 5 0.766 7 1.857 8 2.039 1 0.677 7 26.514 2 136.306 8 3 5 0.800 0 2.039 7 2.039 7 0.679 9 26.570 6 143.639 7 例 3 假设第一类用户请求的到达率不变,分 析第二类用户请求的到达率增大对系统的影响。 假设 h1 = 40,h2 = 20,β = 0.8,N = 100,μ1 = μ2 = 1.5, λ1 = 1,λ2∈[1.25,4]。 首先,对于给定的 λ2 ,通过例 1 的方法求解最优值 c ∗ 。 其次,令 c = c ∗ ,分析系统 的如下性能指标:ρ、E( L1 )、E( L2 )、E( T)、P总 及 f(c ∗ )。 表 3 的数值结果显示,随着 λ2 增大,c ∗ 不 变或增大(如图 4 所示),E( L2 )、P总 及 f( c ∗ )随着 λ2 增大而增大,而 ρ、E(L1 )、E(T)未呈现单调性。 图 3 最优服务器数量(例 2) Fig.3 The optimal number of servers (example 2) 表 3 云计算中心的性能、能耗及成本分析(例 3) Table 3 The performance,power consumption and cost of cloud computing centers (example 3) λ2 c ∗ ρ E(L1 ) E(L2 ) E(T) P总 f(c ∗ ) 1.25 3 0.500 0 0.675 8 0.855 5 0.680 6 13.883 9 55.247 7 1.5 3 0.555 6 0.675 7 1.045 3 0.688 4 14.239 2 59.326 4 1.75 3 0.611 1 0.675 7 1.250 5 0.700 4 14.544 1 63.671 7 2 3 0.666 7 0.675 6 1.477 4 0.717 7 14.806 5 68.417 0 2.25 4 0.541 7 0.667 5 1.544 4 0.680 6 19.968 6 73.563 0 2.5 4 0.583 3 0.667 7 1.739 7 0.687 8 20.211 6 77.671 8 2.75 4 0.625 0 0.667 5 1.947 7 0.697 4 20.418 9 81.991 1 3 4 0.666 7 0.667 5 2.173 3 0.710 2 20.596 2 86.643 5 3.25 4 0.708 3 0.667 5 2.423 2 0.727 2 20.747 8 91.761 8 3.5 5 0.600 0 0.666 6 2.422 9 0.686 6 26.049 0 95.962 8 3.75 5 0.633 3 0.666 7 2.629 8 0.694 0 26.181 1 100.211 5 4 5 0.666 7 0.666 6 2.850 9 0.703 5 26.293 5 104.717 6 第 5 期 张江强,等:具有两类请求的云计算中心服务器数量的优化 ·605·