
(2019春季1 课程编号:011184) © 信息安全导论 第2章密码技术 中国科学枝术大学曾凡平
信息安全导论 第2章 密码技术 中国科学技术大学 曾凡平 (2019春季 课程编号:011184)
第2章密码技术 2.1 2.2 2.3 2.4 2.5 2.6 基 对称 公钥 散列函 数字 密钥管理 概念 密码 密码 数和消 签名 (自学,不考核刻 息认证 古典密码 公钥密码 码 体制原理 数字签名简 公钥分配 分 分组密码 RSA算法 散列函数 对称密码体制 基于公钥密 的密钥分配 码的数字签 消息验证 名原理 序列密码 码 公钥密码用于 对称密码体制 数字签名算 的密钥分配 法 Diffie-Hellman 密钥交换 信息安全导论02 3
第2章 密码技术 2.1 基本 概念 2.2 对称 密码 古典密码 分组密码 序列密码 2.3 公钥 密码 公 钥 密 码 体制原理 RSA算法 2.4 散列函 数和消 息认证 码 散列函数 消 息 验 证 码 2.5 数字 签名 数字签名简 介 基于公钥密 码的数字签 名原理 数字签名算 法 2.6 密钥管理 (自学,不考核) 公钥分配 对 称 密 码 体 制 的密钥分配 公 钥 密 码 用 于 对 称 密 码 体 制 的密钥分配 Diffie-Hellman 密钥交换 信息安全导论02 3

2.1基本概念 密码学=密码编码学+密码分析学 。 密码编码学:研究密码变化的客观规律,设计各 种加密方案,编制密码以保护信息安全的技术。 密码分析学(或密码破译学):在不知道任何加 密细节的条件下,分析、破译经过加密的消息以 获取信息的技术。 ·明文:原始的消息 ·密文:加密后的消息 信息安全导论02 4
2.1 基本概念 • 密码学=密码编码学+密码分析学 • 密码编码学:研究密码变化的客观规律,设计各 种加密方案,编制密码以保护信息安全的技术。 • 密码分析学(或密码破译学):在不知道任何加 密细节的条件下,分析、破译经过加密的消息以 获取信息的技术。 • 明文:原始的消息 • 密文:加密后的消息 信息安全导论02 4
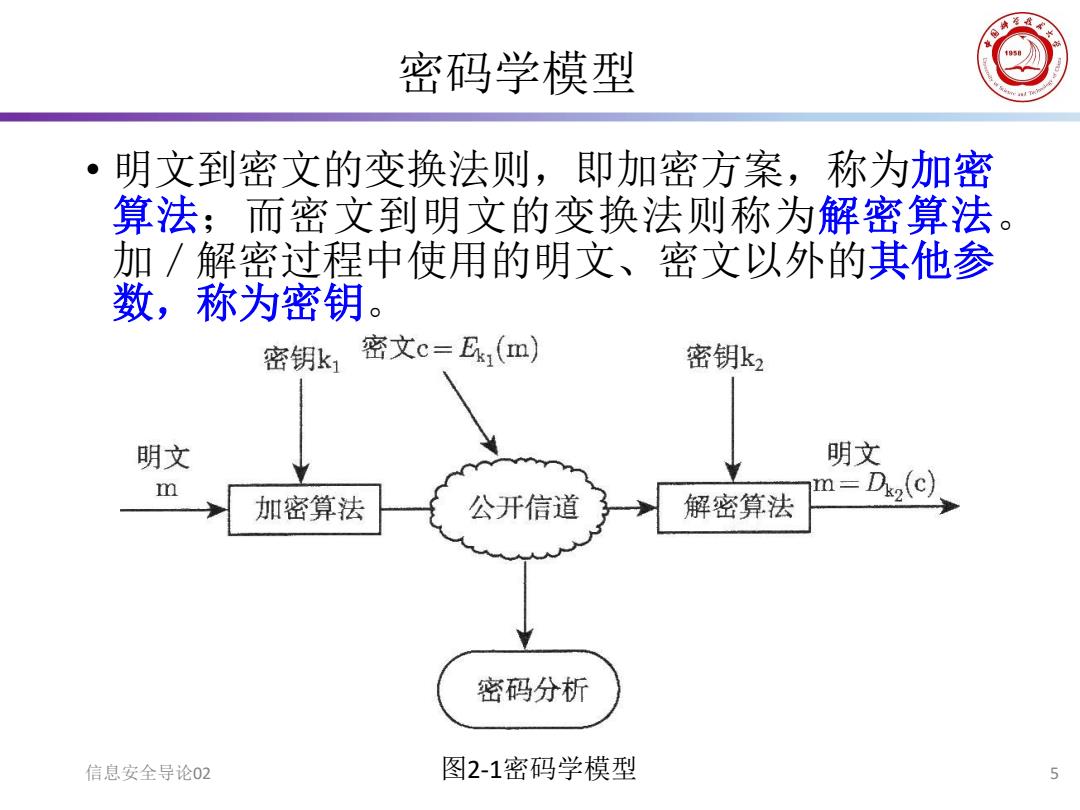
密码学模型 明文到密文的变换法则,即加密方案,称为加密 算法;而密文到明文的变换法则称为解密算法 加/解密过程中使用的明文、密文以外的其他参 数,称为密钥。 密钥k1 密文c=,(m) 密钥k2 明文 明文 m 加密算法 公开信道 解密算法 m=D2(c) 密码分析 信息安全导论02 图2-1密码学模型 5
密码学模型 信息安全导论02 5 • 明文到密文的变换法则,即加密方案,称为加密 算法;而密文到明文的变换法则称为解密算法。 加/解密过程中使用的明文、密文以外的其他参 数,称为密钥。 图2-1密码学模型

密码体制 密码体制:一个用于加解密并能够解决网络安全 中的机密性、完整性、可用性、可控性和真实性 等问题中的一个或几个的系统。 0¥ 密码体制可以定义为一个五元组(P,C,K,E,D) ·P称为明文空间,是所有可能的明文构成的集合: ·C称为密文空间,是所有可能的密文构成的集合: ·K称为密钥空间,是所有可能的密钥构成的集合: ·E和D分别表示加密算法和解密算法的集合,它们满 足: >对每一个k∈K,必然存在一个加密算法e∈E和一个 解密算法d∈D,使得对任意m∈P,恒有dk(ek(m)=m 信息安全导论02 6
密码体制 • 密码体制:一个用于加解密并能够解决网络安全 中的机密性、完整性、可用性、可控性和真实性 等问题中的一个或几个的系统。 • 密码体制可以定义为一个五元组(P, C, K, E, D) • P称为明文空间,是所有可能的明文构成的集合; • C称为密文空间,是所有可能的密文构成的集合; • K称为密钥空间,是所有可能的密钥构成的集合; • E和D分别表示加密算法和解密算法的集合,它们满 足: 对每一个k∈K,必然存在一个加密算法ek∈E和一个 解密算法dk∈D,使得对任意m∈P,恒有dk (ek (m))=m 信息安全导论02 6