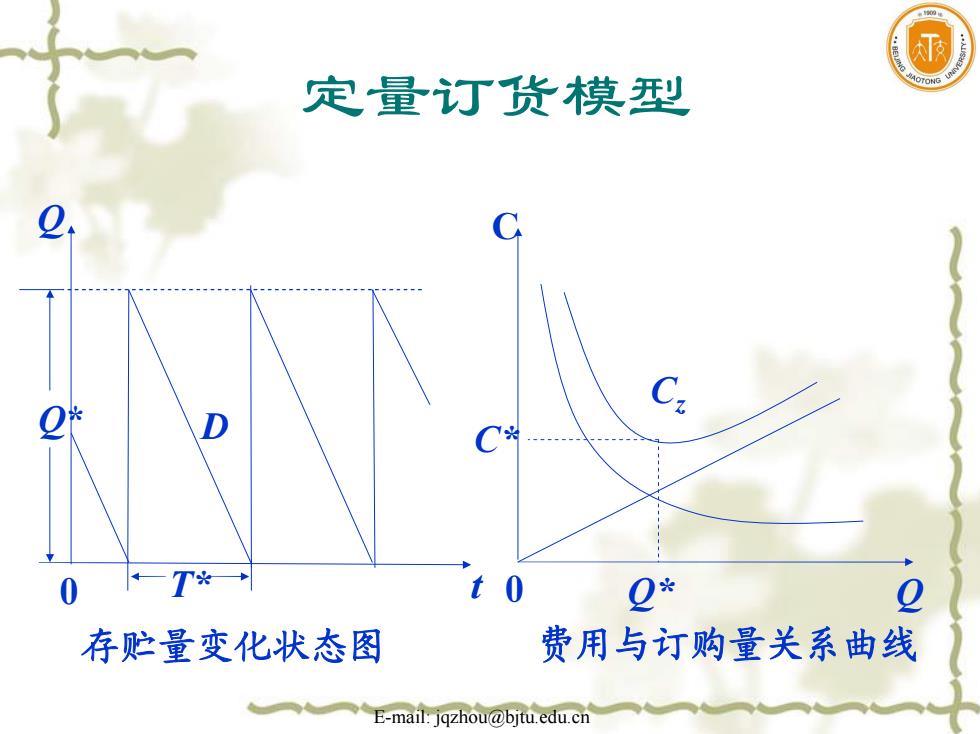
定量灯货模型 D 0 T* t 2* 2 存贮量变化状态图 费用与订购量关系曲线 E-mail:jqzhou@bjtu.edu.cn
Email: jqzhou@bjtu.edu.cn 存贮量变化状态图 Q Q* D 0 T* t C C* C z 0 Q* Q 费用与订购量关系曲线 定量订货模型

模型假设 ”需求稳定 ”订货提前期不变 ”每次订货量不变 每次订货一次入库,入库过程在极短时间内 完成 ”订货成本、胆碱存储成本和单价固定不变 冬不允许出现缺货 E-mail:jqzhou@bjtu.edu.cn
Email: jqzhou@bjtu.edu.cn 模型假设 v 需求稳定 v 订货提前期不变 v 每次订货量不变 v 每次订货一次入库,入库过程在极短时间内 完成 v 订货成本、胆碱存储成本和单价固定不变 v 不允许出现缺货

其存贮参数为: D:单位时间需求量,为常数 T:存贮周期或订货周期; Q:每次订购批量,满足在T时间内的消耗; L:提前订货时间为零,即订货后瞬间全部到货; :存贮单位物资单位时间的存贮费率; P:订购单价 C:每次订货的订货费。 求最佳经济批量EOO,使总的费用TC达到最小。 E-mail:jqzhou@bjtu.edu.cn
Email: jqzhou@bjtu.edu.cn D:单位时间需求量,为常数 T :存贮周期或订货周期; Q:每次订购批量,满足在T时间内的消耗; L :提前订货时间为零,即订货后瞬间全部到货; H:存贮单位物资单位时间的存贮费率; P:订购单价 C:每次订货的订货费。 求最佳经济批量EOQ,使总的费用TC达到最小。 其存贮参数为:

一个存贮周期内 年订货费:CD/Q 年存贮费:1/2PHQ 单位时间的存贮总费用为 TC=1/2PHQ +CD/Q 利用微分求极值的方法即得到经济订购批量 (威尔逊公式) 2CD 例题见教材 PH E-mail:jqzhou@bjtu.edu.cn
Email: jqzhou@bjtu.edu.cn 一个存贮周期内 年订货费:CD/Q 年存贮费:1/2PHQ 单位时间的存贮总费用为 TC=1/2PHQ +CD/Q PH CD Q 2 * = 利用微分求极值的方法即得到经济订购批量 (威尔逊公式) 例题见教材

价格有折扣的EOQ模型 单价有n级折扣,第一级规定的最低一次订购量最 小,(一般可以从零开始),单价最高,以后各级规定 的最低一次订购量逐级增加,而单价逐级降低,令 V,—第j级的物资单价(V1>V); Q,一第j+1级的最低一次订购量(Q,<Q1); Q— 实际一次订购量,则当Q1≤Q<Q时,单 价为V,购货款为QV 按这种折扣形式,所订购的物资,整批按一个统 一单价计算货款。 E-mail:jqzhou@bjtu.edu.cn
Email: jqzhou@bjtu.edu.cn 单价有 n 级折扣,第一级规定的最低一次订购量最 小,(一般可以从零开始),单价最高,以后各级规定 的最低一次订购量逐级增加,而单价逐级降低,令 Vj —— 第j级的物资单价(Vj1 > V j ); Qj —— 第j+1级的最低一次订购量( Qj < Q j+1); Q —— 实际一次订购量,则当Qj1 £Q < Qj 时,单 价为Vj ,购货款为Q• Vj 按这种折扣形式,所订购的物资,整批按一个统 一单价计算货款。 价格有折扣的EOQ模型