
效绵鼎 Converting a RE to an E-NFA Proof is an induction on the number of operators (+ concatenation,*in the RE ■ We always construct an automaton of a special form (next slide) .11
11 Converting a RE to an ε-NFA ◼ Proof is an induction on the number of operators (+, concatenation, *) in the RE. ◼ We always construct an automaton of a special form (next slide)
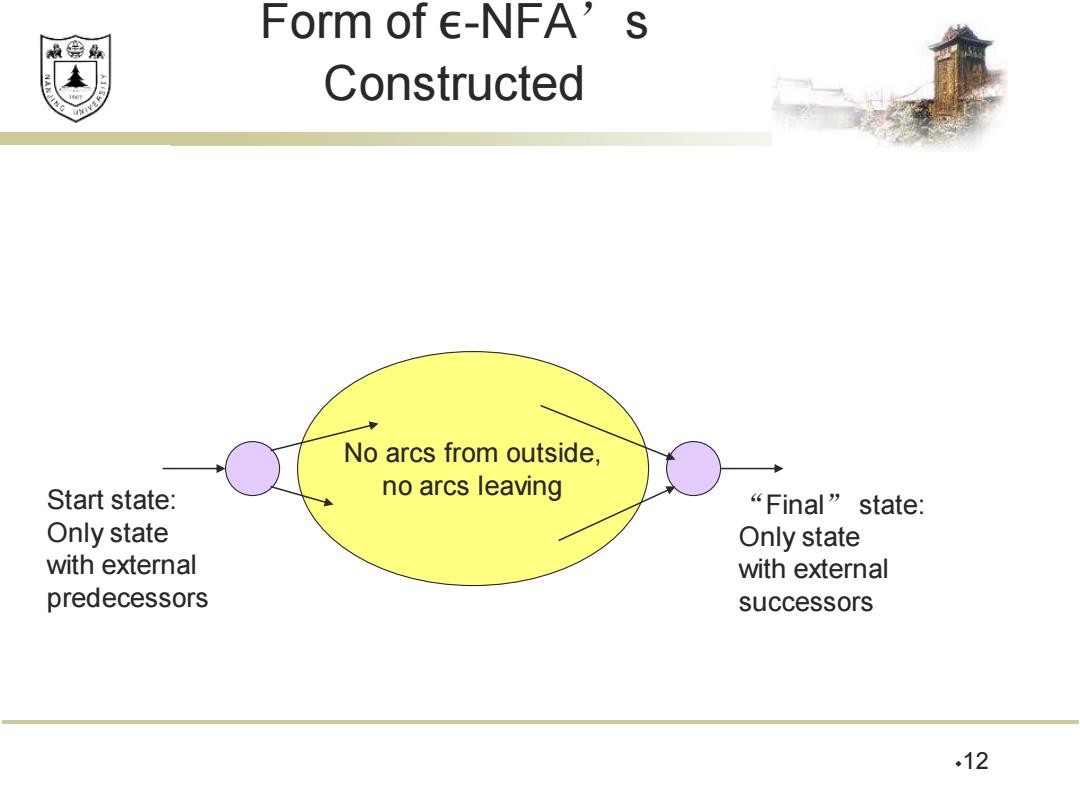
Form of e-NFA’s 效绵鼎 Constructed No arcs from outside, Start state: no arcs leaving “Final” state: Only state Only state with external with external predecessors successors .12
12 Form of ε-NFA’s Constructed No arcs from outside, no arcs leaving Start state: Only state with external predecessors “Final” state: Only state with external successors
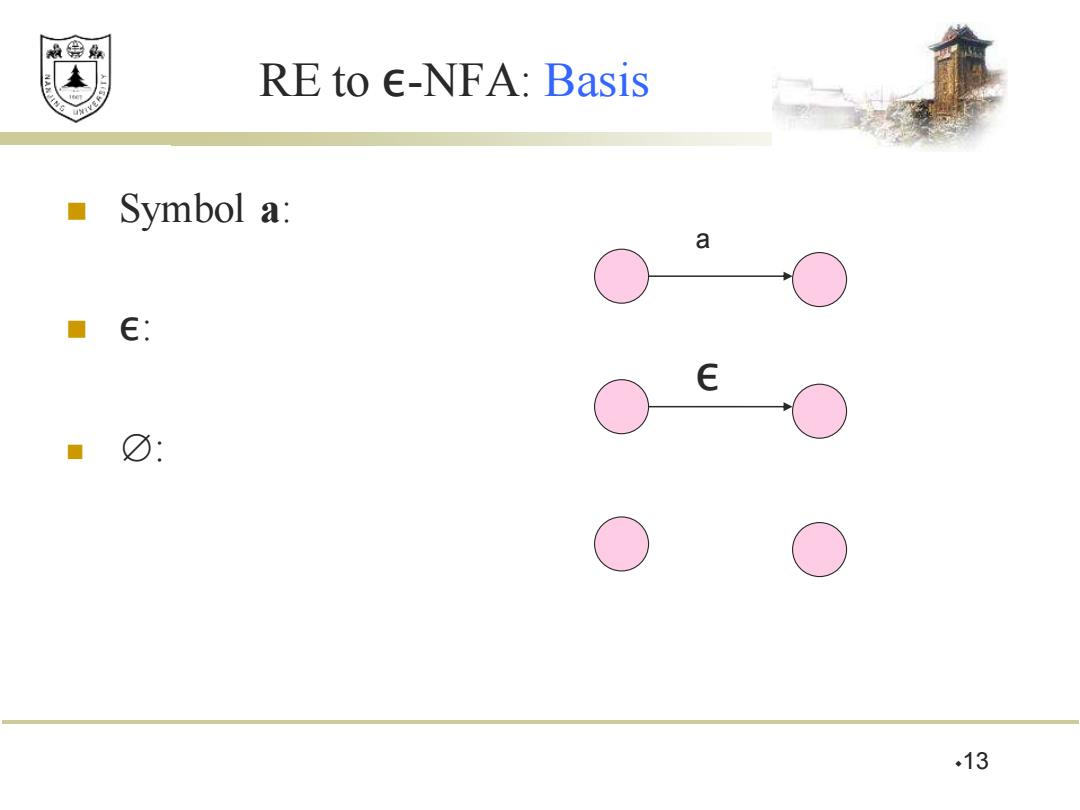
效绵鼎 RE to E-NFA:Basis ■ Symbol a: a ■€: E C ☑: ○ ○ ○ .13
13 RE to ε-NFA: Basis ◼ Symbol a: ◼ ε: ◼ ∅: a ε
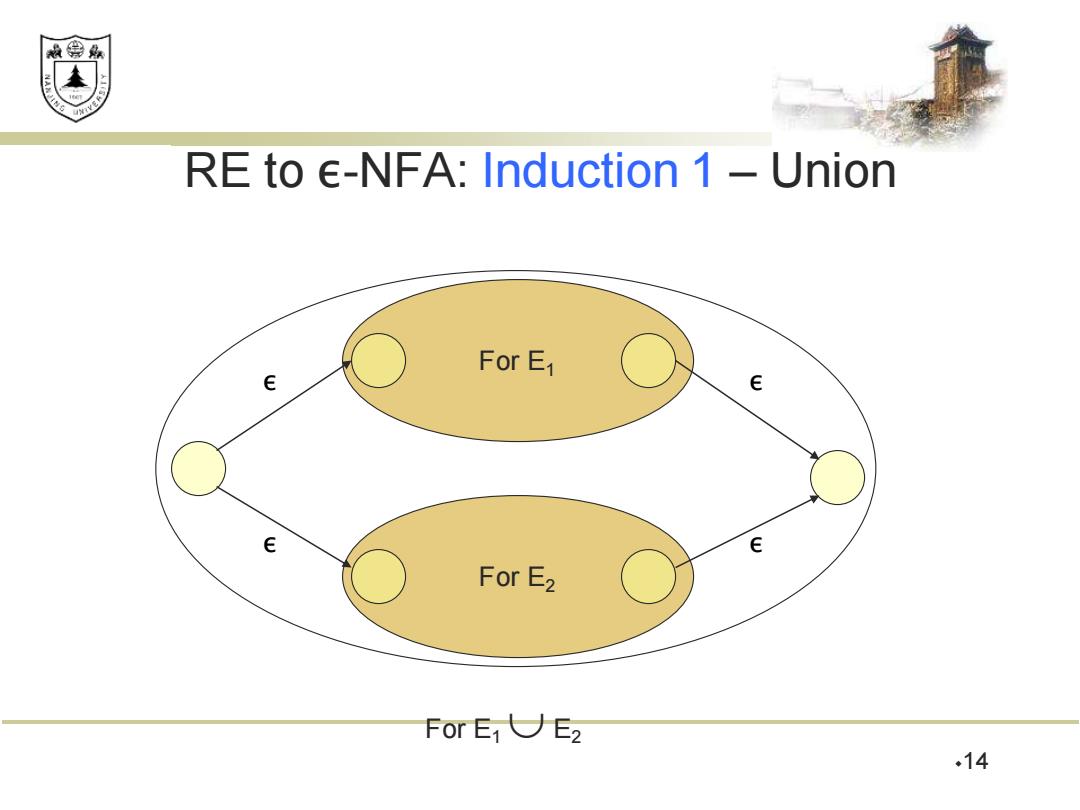
效绵县 RE to E-NFA:Induction 1 -Union For E1 For E2 ForE1弋∪E2 .14
14 RE to ε-NFA: Induction 1 – Union For E1 For E2 For E1 E2 ε ε ε ε
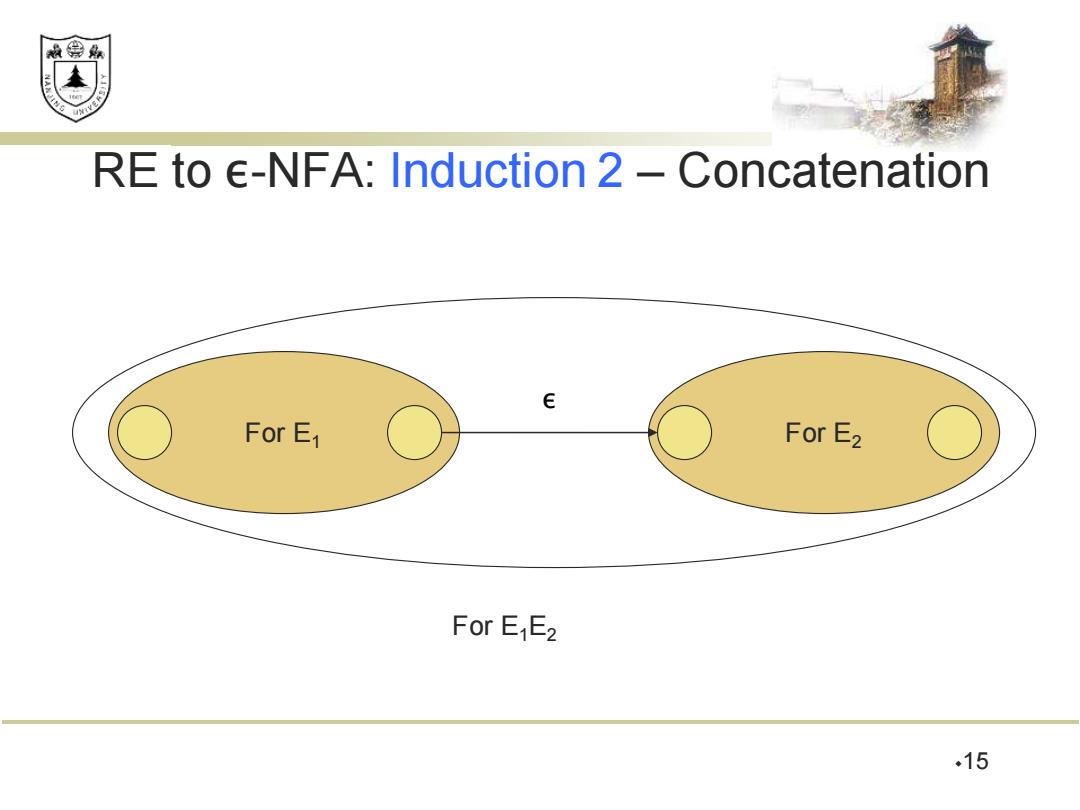
效绵县 RE to e-NFA:Induction 2 -Concatenation E For E1 For E2 For EE2 .15
15 RE to ε-NFA: Induction 2 – Concatenation For E1 For E2 For E1E2 ε