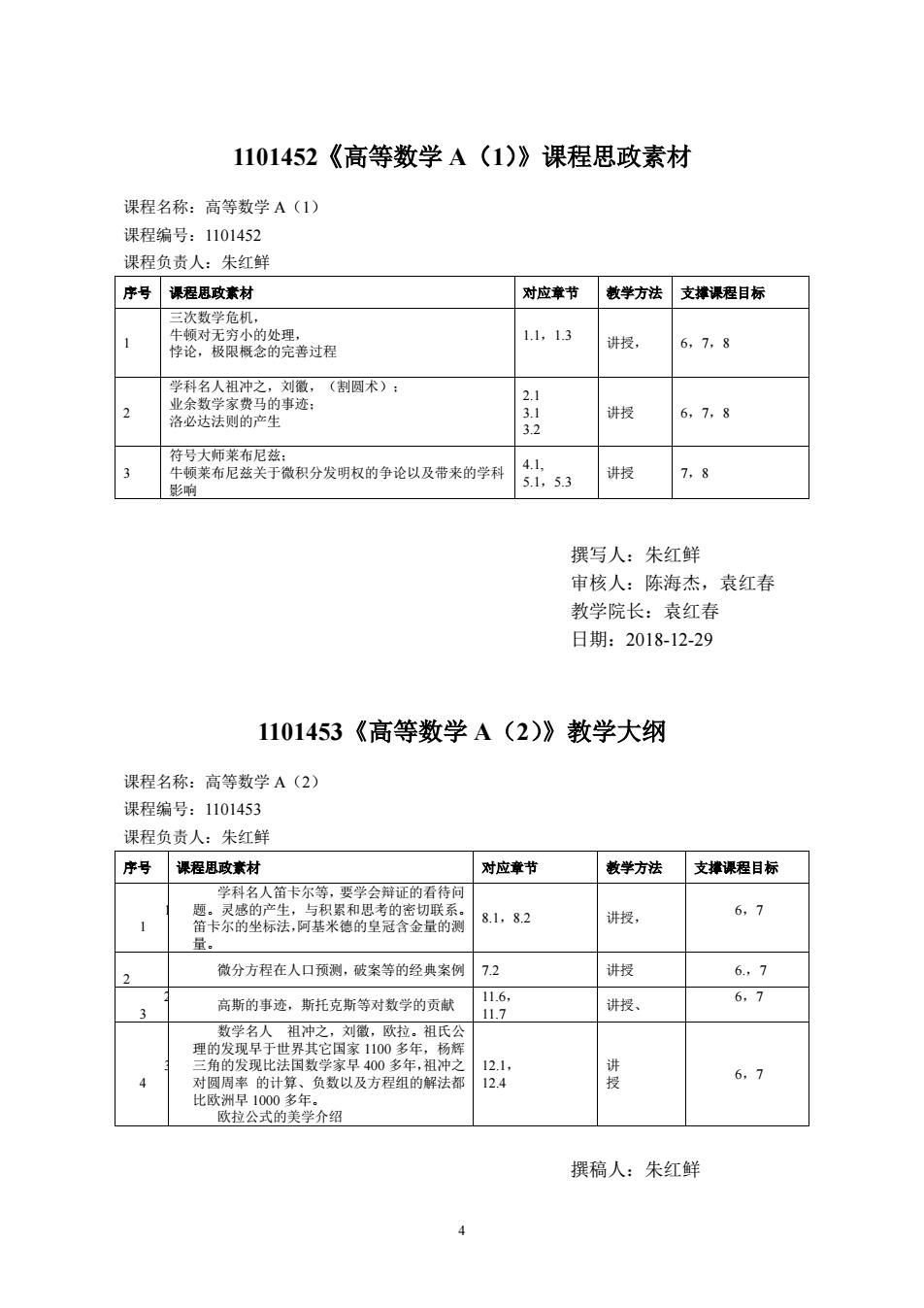
1101452《高等数学A(1)》课程思政素材 课程名称:高等数学A(1) 课程编号:1101452 课程负责人:朱红鲜 序号课程思政素材 对应章节敏学方法支排课程目标 1.1,13 讲授, 6,7,8 (割圆术): 洛必达法则的产生 1112 讲授 6,7,8 关学微积分发明收的争论以及来的学科 ,53 讲授 7,8 撰写人:朱红鲜 审核人:陈海杰,袁红春 教学院长:袁红春 日期:2018-12-29 1101453《高等数学A(2)》教学大纲 课程名称:高等数学A(2) 课程编号:1101453 课程负责人:朱红鲜 序号课程思政素材 对应章节 教学方法支排课程目标 学科名人前卡 等 证的看》 8.1,8.2 讲授, 6,7 微分方程在人口预测,破案等的经典案例7.2 讲授 67 6,7 3 高斯的事迹,斯托克斯等对数学的贡献 讲投 理的发 数以及方程组的解法都 讲授 6,7 撰稿人:朱红鲜
4 1101452《高等数学 A(1)》课程思政素材 课程名称:高等数学 A(1) 课程编号:1101452 课程负责人:朱红鲜 序号 课程思政素材 对应章节 教学方法 支撑课程目标 1 三次数学危机, 牛顿对无穷小的处理, 悖论,极限概念的完善过程 1.1,1.3 讲授, 6,7,8 2 学科名人祖冲之,刘徽,(割圆术); 业余数学家费马的事迹; 洛必达法则的产生 2.1 3.1 3.2 讲授 6,7,8 3 符号大师莱布尼兹; 牛顿莱布尼兹关于微积分发明权的争论以及带来的学科 影响 4.1, 5.1,5.3 讲授 7,8 撰写人:朱红鲜 审核人:陈海杰,袁红春 教学院长:袁红春 日期:2018-12-29 1101453《高等数学 A(2)》教学大纲 课程名称:高等数学 A(2) 课程编号:1101453 课程负责人:朱红鲜 序号 课程思政素材 对应章节 教学方法 支撑课程目标 1 1 学科名人笛卡尔等,要学会辩证的看待问 题。灵感的产生,与积累和思考的密切联系。 笛卡尔的坐标法,阿基米德的皇冠含金量的测 量。 8.1,8.2 讲授, 6,7 2 微分方程在人口预测,破案等的经典案例 7.2 讲授 6.,7 2 3 高斯的事迹,斯托克斯等对数学的贡献 11.6, 11.7 讲授、 6,7 3 4 数学名人 祖冲之,刘徽,欧拉。祖氏公 理的发现早于世界其它国家 1100 多年,杨辉 三角的发现比法国数学家早 400 多年,祖冲之 对圆周率 的计算、负数以及方程组的解法都 比欧洲早 1000 多年。 欧拉公式的美学介绍 12.1, 12.4 讲 授 6,7 撰稿人:朱红鲜

审核人:陈海杰,袁红春 教学院长:袁红春 2018年12月29日 1101454《高等数学B(1)》课程思政素材 课程名称:高等数学B() 课程编号:1101454 课程负责人:李英杰 序号 课程思政素材 对应章节 教学方法 支排课程目标 4 数学思起·数学素质和素养,极限、退 讲授,课堂讨论 增强民族白象 第一章第二节 讲授 第三章第一节 讲授 课堂讨论 讨论 讲授、讨论 拉格 第五章第二节 7 文关怀,极值,最 值,人生的喻峰和低 第三章第五节 讲投 撰写人:李英杰 审核人:陈海杰,袁红春 教学院长:袁红春 日期:2018年12月29日
5 审核人:陈海杰,袁红春 教学院长:袁红春 2018 年 12 月 29 日 1101454《高等数学 B(1)》课程思政素材 课程名称:高等数学 B(1) 课程编号:1101454 课程负责人:李英杰 序号 课程思政素材 对应章节 教学方法 支撑课程目标 3 4 1 数学思想,数学素质和素养,极限、逼 近,变换、优化思想 第一章第二、三节 第五章 第三节 讲授,课堂讨论 √ 2 增强民族自豪感,激发爱国热情,庄周 的《庄子天下篇》一尺之锤,日取其半, 万事不竭 第一章第二节 讲授 √ √ 3 脚踏实地、诚信做人的人生观、价值观, 拉格朗日定理满足条件的演绎推理过 程的严密性和精确性 第三章第一节 讲授 √ 4 辩证思维,连续性与间断性,可导与不 可导,不定积分与定积分 第一章第八节 第二章第一节 第四章第一节 第五章第一节 课堂讨论 √ 5 社会责任感,民族凝聚力,微积分的发 展史,近代中国数学史 第二章第一节 第四章第一节 讨论 √ 6 严谨求实的科学态度,创新精神,激发 学习动力,数学名人欧拉、牛顿、莱布 尼茨、柯西、拉格朗日 第三章第一节 第七章第九节 第五章第二节 讲授、讨论 √ 7 人生观、价值观,人文关怀,极值,最 值,人生的巅峰和低谷 第三章第五节 讲授 √ 撰写人:李英杰 审核人:陈海杰,袁红春 教学院长:袁红春 日 期:2018 年 12 月 29 日
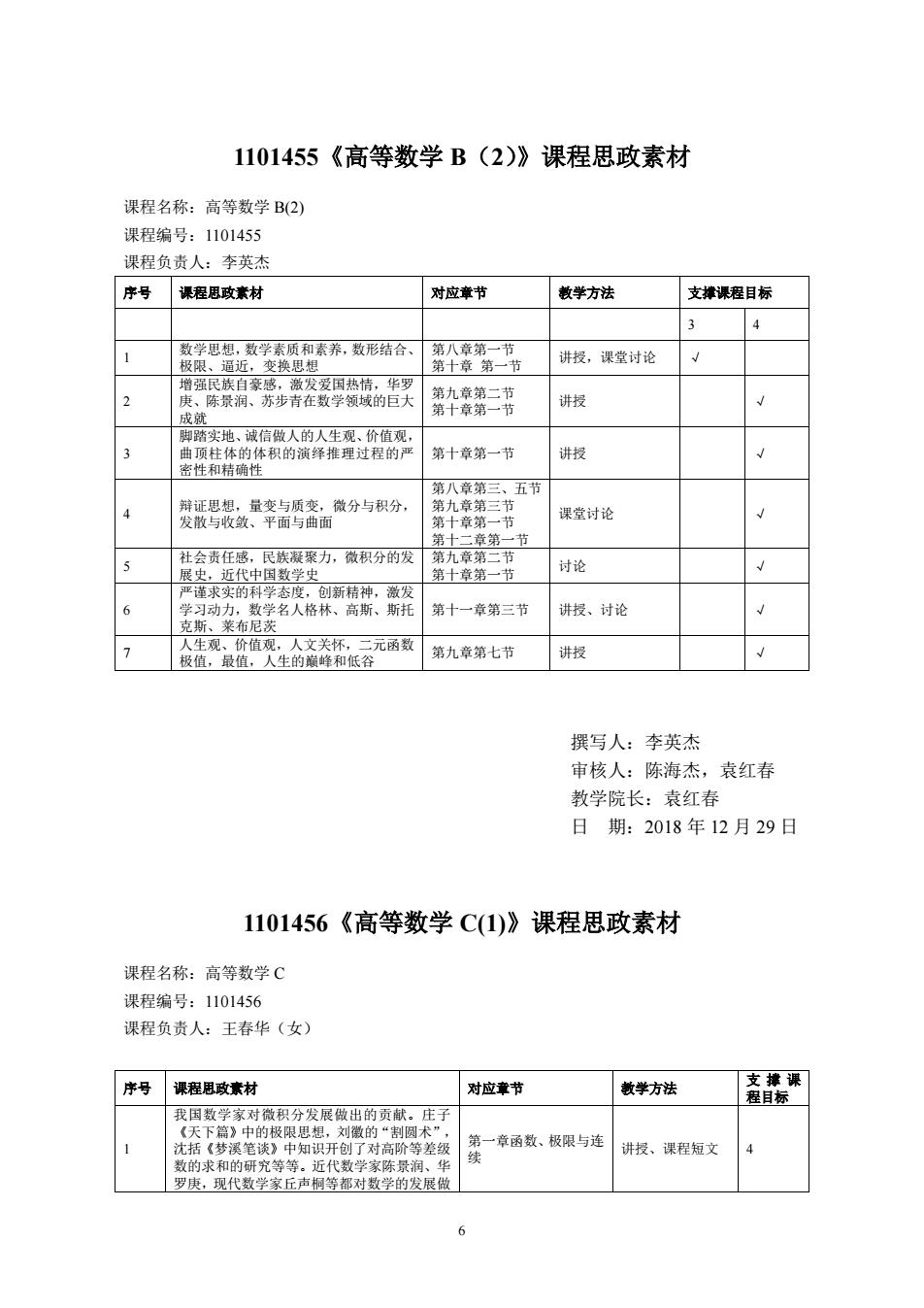
1101455《高等数学B(2)》课程思政素材 课程名称:高等数学B(2) 课程编号:1101455 课程负责人:李英杰 序号课程思政素材 对应章节 敦学方法 支撞课程目标 3 4 数学思想,数学 和素养,数形结合、 讲授,课逢讨论 换思 补书 讲授 脚实地、诚信做人的人生观、价值 盟修的作积的清绎推理过程的 第十章第一节 讲 五节 赞号提量喜分与积分 章 三 课堂讨论 社会责任感,民族凝聚力,微积分的发 讨论 √ 子习动 第十一章第三节 讲授、讨论 第九章第七节 撰写人:李英杰 审核人:陈海杰,袁红春 教学院长:袁红春 日期:2018年12月29日 1101456《高等数学C(1)》课程思政素材 课程名称:高等数学 课程编号:1101456 课程负责人:王春华(女) 序号课程思政素材 对应幸节 教学方法 思想,刘的 一章函数、极限与 井授、课程短文
6 1101455《高等数学 B(2)》课程思政素材 课程名称:高等数学 B(2) 课程编号:1101455 课程负责人:李英杰 序号 课程思政素材 对应章节 教学方法 支撑课程目标 3 4 1 数学思想,数学素质和素养,数形结合、 极限、逼近,变换思想 第八章第一节 第十章 第一节 讲授,课堂讨论 √ 2 增强民族自豪感,激发爱国热情,华罗 庚、陈景润、苏步青在数学领域的巨大 成就 第九章第二节 第十章第一节 讲授 √ 3 脚踏实地、诚信做人的人生观、价值观, 曲顶柱体的体积的演绎推理过程的严 密性和精确性 第十章第一节 讲授 √ 4 辩证思想,量变与质变,微分与积分, 发散与收敛、平面与曲面 第八章第三、五节 第九章第三节 第十章第一节 第十二章第一节 课堂讨论 √ 5 社会责任感,民族凝聚力,微积分的发 展史,近代中国数学史 第九章第二节 第十章第一节 讨论 √ 6 严谨求实的科学态度,创新精神,激发 学习动力,数学名人格林、高斯、斯托 克斯、莱布尼茨 第十一章第三节 讲授、讨论 √ 7 人生观、价值观,人文关怀,二元函数 极值,最值,人生的巅峰和低谷 第九章第七节 讲授 √ 撰写人:李英杰 审核人:陈海杰,袁红春 教学院长:袁红春 日 期:2018 年 12 月 29 日 1101456《高等数学 C(1)》课程思政素材 课程名称:高等数学 C 课程编号:1101456 课程负责人:王春华(女) 序号 课程思政素材 对应章节 教学方法 支 撑 课 程目标 1 我国数学家对微积分发展做出的贡献。庄子 《天下篇》中的极限思想,刘徽的“割圆术”, 沈括《梦溪笔谈》中知识开创了对高阶等差级 数的求和的研究等等。近代数学家陈景润、华 罗庚,现代数学家丘声桐等都对数学的发展做 第一章函数、极限与连 续 讲授、课程短文 4
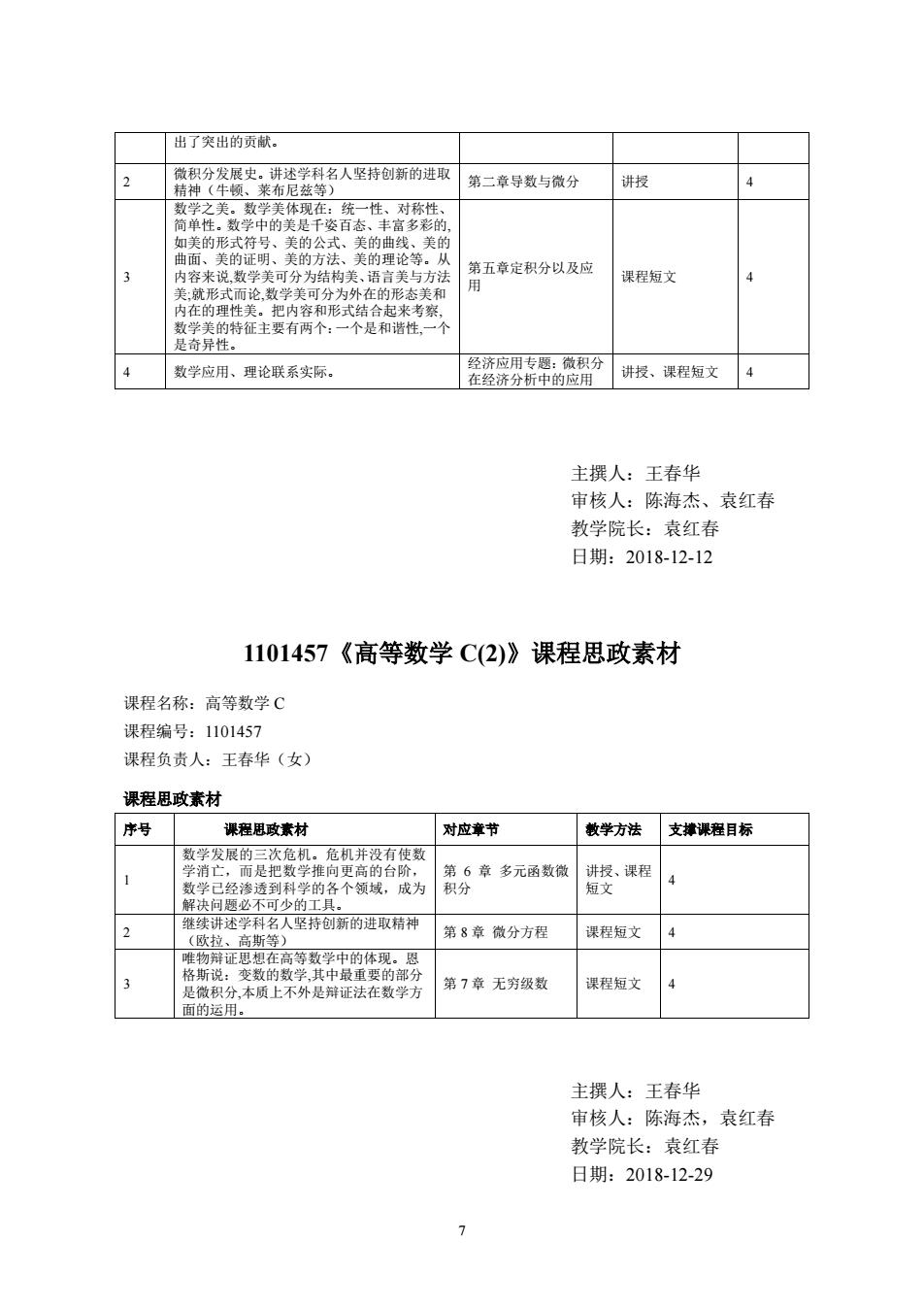
出了突出的贡献。 讲授 的龙 的正 笔的 来说数 第五章定积分以及应 分为结构美,语言关 课程短文 4 用 把内容和形 是奇异性。 数学应用、理论联系实际。 讲授、课程短文 4 主撰人:王春华 审核人:陈海杰、袁红春 教学院长:袁红春 日期:2018-12-12 1101457《高等数学C(2)》课程思政素材 课程名称:高等数学C 课程编号:1101457 课程负责人:王春华(女) 课程思政素材 序号 课程思政素材 对应章节 教学方法支排课程目标 数子发展的济机:机并没有使数 秀到 解决问 的各个领域,成为 费程 科名人坚持创新的进取精衬 第8章微分方程 课程短文 等数学中的体现, ,本质上不外是证的} 第7章无穷级数 保程短文 面的运用 主耀人:王春华 审核人:陈海杰,袁红春 教学院长:袁红春 日期:2018-12-29
7 出了突出的贡献。 2 微积分发展史。讲述学科名人坚持创新的进取 精神(牛顿、莱布尼兹等) 第二章导数与微分 讲授 4 3 数学之美。数学美体现在:统一性、对称性、 简单性。数学中的美是千姿百态、丰富多彩的, 如美的形式符号、美的公式、美的曲线、美的 曲面、美的证明、美的方法、美的理论等。从 内容来说,数学美可分为结构美、语言美与方法 美;就形式而论,数学美可分为外在的形态美和 内在的理性美。把内容和形式结合起来考察, 数学美的特征主要有两个:一个是和谐性,一个 是奇异性。 第五章定积分以及应 用 课程短文 4 4 数学应用、理论联系实际。 经济应用专题:微积分 在经济分析中的应用 讲授、课程短文 4 主撰人:王春华 审核人:陈海杰、袁红春 教学院长:袁红春 日期:2018-12-12 1101457《高等数学 C(2)》课程思政素材 课程名称:高等数学 C 课程编号:1101457 课程负责人:王春华(女) 课程思政素材 序号 课程思政素材 对应章节 教学方法 支撑课程目标 1 数学发展的三次危机。危机并没有使数 学消亡,而是把数学推向更高的台阶, 数学已经渗透到科学的各个领域,成为 解决问题必不可少的工具。 第 6 章 多元函数微 积分 讲授、课程 短文 4 2 继续讲述学科名人坚持创新的进取精神 (欧拉、高斯等) 第 8 章 微分方程 课程短文 4 3 唯物辩证思想在高等数学中的体现。恩 格斯说:变数的数学,其中最重要的部分 是微积分,本质上不外是辩证法在数学方 面的运用。 第 7 章 无穷级数 课程短文 4 主撰人:王春华 审核人:陈海杰,袁红春 教学院长:袁红春 日期:2018-12-29

1101458《高等数学(1)》课程思政素材 课程名称:高等数学() 课程编号:1101458 课程负责人:刘太岗 内容一、我国数学家对微积分发展做出的贡献。 祖氏公理的发现早于世界其它国家1100多年,杨辉三角的发现比法国数学家早400多年, 祖冲之对圆周率的计算、负数以及方程组的解法都比欧洲早1000多年。近代的徐光启、李善兰 及当代的华罗庚、陈景润等,在他们所研究的领域中都对数学作出了独特的贡献。这些其实典型 的事不仅可以溜发学生强列的爱国主义热情和民族白意感,而目也能激励学生学习的讲取结神, 内容二、数学发展史上的三次危机。 从无理数的出现,到极限理论的建立,再到悖论的消亡,数学没有消亡,每一次危机都使数 学获得了更强的生命力。以此渗透危机与机遇并存的思想,在复杂的国际国内形势面前,党中央 国务院带领和团结全国各族人民,不动摇、不折腾、坚持科学发展观,聚精会神搞建设,一心 意谋发展。我们会面临更多的桃战,各种不确定因素使得我们的前进道路更加曲折艰险,山穷水 复时我们不会丧失信心,柳暗花明中我们会看到更多的希望。 耀写人:刘太岗 审核人:陈海杰,袁红春 教学院长:袁红春 日期:2018-12-17 1101459《高等数学(2)》课程思政素材 课程名称:高等数学(2) 课程编号:1101459 课程负责人:刘太岗 内容一:数学中蕴含的辩证唯物主义思想 恩格斯曾经指出:“现实世界的辩证法在数学概念和公式中能得到自己的反映,学生到处都 能遇到辩证法这些规律的表现。”例如,有限与无限、连续与间断、直线与曲线、近似与精确、 微分和积分、收敛与发散、未知与已知、相等与不等、常量与变量等。如我们在解某些系数中含 有字母的方程时,可视未知数为已知数,已知数为未知数:在处理含有参变数的问题时,参变数 既是变数,又是常数。刘徽在割圆术中指出:随着圆内接正多边形边数的增加,它的周长和面积 越来越接近圆周长和圆面积。采用这种“化圆为方”、“化曲为直”的极限思想,通过观察“有限 分割”,想象“无限细分”,根据图形分割拼合的变化趋势想象它们的终极状态,不仅求出了圆的
8 1101458《高等数学(1)》课程思政素材 课程名称:高等数学(1) 课程编号:1101458 课程负责人:刘太岗 内容一、我国数学家对微积分发展做出的贡献。 祖氏公理的发现早于世界其它国家 1100 多年,杨辉三角的发现比法国数学家早 400 多年, 祖冲之对圆周率 的计算、负数以及方程组的解法都比欧洲早 1000 多年。近代的徐光启、李善兰 及当代的华罗庚、陈景润等,在他们所研究的领域中都对数学作出了独特的贡献。这些真实典型 的事例不仅可以激发学生强烈的爱国主义热情和民族自豪感,而且也能激励学生学习的进取精神。 内容二、数学发展史上的三次危机。 从无理数的出现,到极限理论的建立,再到悖论的消亡,数学没有消亡,每一次危机都使数 学获得了更强的生命力。以此渗透危机与机遇并存的思想,在复杂的国际国内形势面前,党中央 国务院带领和团结全国各族人民,不动摇、不折腾、坚持科学发展观,聚精会神搞建设,一心一 意谋发展。我们会面临更多的挑战,各种不确定因素使得我们的前进道路更加曲折艰险,山穷水 复时我们不会丧失信心,柳暗花明中我们会看到更多的希望。 撰写人:刘太岗 审核人:陈海杰,袁红春 教学院长:袁红春 日期:2018-12-17 1101459《高等数学(2)》课程思政素材 课程名称:高等数学(2) 课程编号:1101459 课程负责人:刘太岗 内容一:数学中蕴含的辩证唯物主义思想 恩格斯曾经指出:“现实世界的辩证法在数学概念和公式中能得到自己的反映,学生到处都 能遇到辩证法这些规律的表现。”例如,有限与无限、连续与间断、直线与曲线、近似与精确、 微分和积分、收敛与发散、未知与已知、相等与不等、常量与变量等。如我们在解某些系数中含 有字母的方程时,可视未知数为已知数,已知数为未知数;在处理含有参变数的问题时,参变数 既是变数,又是常数。刘徽在割圆术中指出:随着圆内接正多边形边数的增加,它的周长和面积 越来越接近圆周长和圆面积。采用这种“化圆为方”、“化曲为直”的极限思想,通过观察“有限 分割”,想象“无限细分”,根据图形分割拼合的变化趋势想象它们的终极状态,不仅求出了圆的