
5208402《逻辑与计算机设计基础1课程设计》课程思政素材 .101 5208403《人工智能基础》课程思政素材 .102 5208404《人工智能基础课程设计》课程思政素材 102 5208405《数学建模》课程思政素材 103 5208406《数学建模课程设计》课程思政素材 104 5208407《数学实验》课程思政素材 l04 5208408《数值分析》课程思政素材 4l05 5208409《数值分析课程设计实习》课程思政素材 106 5208410《数字信号处理课程设计》课程思政素材 106 5208411《算法基础》课程思政素材 107 5208412《算法基础课程设计》课程思政素材. 108 5208413《微分方程数值解》思政素材 ,108 5208414《微机原理与接口技术》课程思政素材 109 5208415《微机原理与接口技术》课程思政素材 .110 5208416《物联网概论》课程思政素材 110 5208551《软件工程》课程思政素材 111 5208552《软件工程Ⅱ》课程思政素材 .112 5208553《软件工程Ⅱ》理论课课程思政素材 112 5208554《软件工程II》课程思政素材 .113 5208555《软件工程Ⅲ》课程思政素材 113 5208556《软件工程Ⅲ课程设计》课程思政素材 114 5208557《软件工程Ⅱ》课程设计课程思政素材. 5208558《软件工程IV》教学大纲课程思政素材 115 5208559实验教学大纲(课程思政素材) .116 5208560《软件工程I课程设计》课程思政素材. 116 5208561《软件工程导论课程设计》教学大纲课程思政素材 .117
VI 5208402《逻辑与计算机设计基础 I 课程设计》课程思政素材................................. 101 5208403《人工智能基础》课程思政素材.................................................................... 102 5208404《人工智能基础课程设计》课程思政素材.................................................... 102 5208405《数学建模》课程思政素材............................................................................ 103 5208406《数学建模课程设计》课程思政素材............................................................ 104 5208407《数学实验》课程思政素材............................................................................ 104 5208408《数值分析》课程思政素材............................................................................ 105 5208409《数值分析课程设计实习》课程思政素材.................................................... 106 5208410《数字信号处理课程设计》课程思政素材.................................................... 106 5208411《算法基础》课程思政素材 ............................................................................ 107 5208412《算法基础课程设计》课程思政素材............................................................ 108 5208413《微分方程数值解》思政素材........................................................................ 108 5208414《微机原理与接口技术》课程思政素材........................................................ 109 5208415《微机原理与接口技术》课程思政素材........................................................ 110 5208416《物联网概论》课程思政素材........................................................................ 110 5208551《软件工程 I》课程思政素材...........................................................................111 5208552《软件工程Ⅱ》课程思政素材........................................................................ 112 5208553《软件工程Ⅱ》理论课 课程思政素材.......................................................... 112 5208554《软件工程 III》课程思政素材....................................................................... 113 5208555《软件工程 III》课程思政素材....................................................................... 113 5208556《软件工程 III 课程设计》课程思政素材...................................................... 114 5208557《软件工程Ⅱ》课程设计 课程思政素材...................................................... 115 5208558《软件工程Ⅳ》教学大纲 课程思政素材...................................................... 115 5208559 实验教学大纲(课程思政素材) ........................................................................ 116 5208560《软件工程 I 课程设计》课程思政素材......................................................... 116 5208561《软件工程导论课程设计》教学大纲 课程思政素材.................................. 117

5208562《软件工程导论》教学大纲课程思政素材. 5208563《软件工程导论课程设计》教学大纲课程思政素材. 118 5208564《软件工程课程设计》课程思政素材 .po 5208565《软件工程综合课程设计》课程思政素材…120 5208566《软件开发与创新》课程思政素材 120 5208567《软件开发与创新课程设计》课程思政素材. …121 5209909《数学专业英语》课程思政素材 121 5208401《控制论基础》课程思政素材.… 122
VII 5208562《软件工程导论》教学大纲 课程思政素材.................................................. 118 5208563《软件工程导论课程设计》教学大纲 课程思政素材.................................. 118 5208564《软件工程课程设计》课程思政素材............................................................ 119 5208565《软件工程综合课程设计》课程思政素材.................................................... 120 5208566《软件开发与创新》课程思政素材................................................................ 120 5208567《软件开发与创新课程设计》课程思政素材................................................ 121 5209909《数学专业英语》课程思政素材.................................................................... 121 5208401《控制论基础》课程思政素材........................................................................ 122

1101407《高等数学T》课程思政素材 课程名称:高等数学T 课程编号:1101407 课程负责人:陈海杰 课程思政素材 内容一、数学发展史上的三次危机 第一次数学危机一—无理数的发现 打破了字宙间一切事物都可归结为整数或整数之比的观念,正明并确定了无理数的存在。 第二次数学危机一无穷小是零吗? 将微积分从强调形式的计算,转为关注计算场景基础使微积分更加完善和取得了广泛应用 第三次数学危机一一悖论的产生 发现集合论的漏洞,集合论在此基础上严谨和完善,促进了集合论的发展。 数学的三次危机从本质上,都是人类孜孜不倦的追求真理、严谨对待科学理论,从而促进科 学技术发展的过程。通过数学发展史上的三次危机,使学生明白,在学习过程中,我们会面临许 多的困难与挑战,培养学生在危机面前不退缩、迎难而上和持之以恒地精神。 内容二、线面积分“变与不变”、“近似与精确”数学原理包含舞证唯物主义思想 培养学生“变与不变”、“近似与精确”、“有限与无限”、“量变与质变”等辩证唯物主义思想 及创造性思维。 内容三、数学的应用 马克思说:“一门科学只有当它达到了能够成功地运用数学时,才算真正发展了。”在前几次 科技革命中,数学大都起到先导与支柱作用。近年来随着科技发展,数学己渗透在自然科学、社 会科学、人文科学中。通过了解线面积分在物理学的应用,了解数学来源于实际问题,使学生多 观察、勤思考,注重创造性思维的训练,遂步养成理论联系实际的学习风格。 撰写人:陈海杰 审核人:刘太岗,袁红春 教学院长:袁红春 日期:2018-12-29
1 1101407《高等数学 T》课程思政素材 课程名称:高等数学 T 课程编号:1101407 课程负责人:陈海杰 课程思政素材 内容一、数学发展史上的三次危机 第一次数学危机──无理数的发现 打破了宇宙间一切事物都可归结为整数或整数之比的观念,证明并确定了无理数的存在。 第二次数学危机──无穷小是零吗? 将微积分从强调形式的计算,转为关注计算场景基础使微积分更加完善和取得了广泛应用。 第三次数学危机——悖论的产生 发现集合论的漏洞,集合论在此基础上严谨和完善,促进了集合论的发展。 数学的三次危机从本质上,都是人类孜孜不倦的追求真理、严谨对待科学理论,从而促进科 学技术发展的过程。通过数学发展史上的三次危机,使学生明白,在学习过程中,我们会面临许 多的困难与挑战,培养学生在危机面前不退缩、迎难而上和持之以恒地精神。 内容二、线面积分“变与不变”、“近似与精确”数学原理包含辩证唯物主义思想 培养学生“变与不变”、“近似与精确”、“有限与无限”、“量变与质变”等辩证唯物主义思想 及创造性思维。 内容三、数学的应用 马克思说:“一门科学只有当它达到了能够成功地运用数学时,才算真正发展了。”在前几次 科技革命中,数学大都起到先导与支柱作用。近年来随着科技发展,数学已渗透在自然科学、社 会科学、人文科学中。通过了解线面积分在物理学的应用,了解数学来源于实际问题,使学生多 观察、勤思考,注重创造性思维的训练,逐步养成理论联系实际的学习风格。 撰写人:陈海杰 审核人:刘太岗,袁红春 教学院长:袁红春 日期:2018-12-29
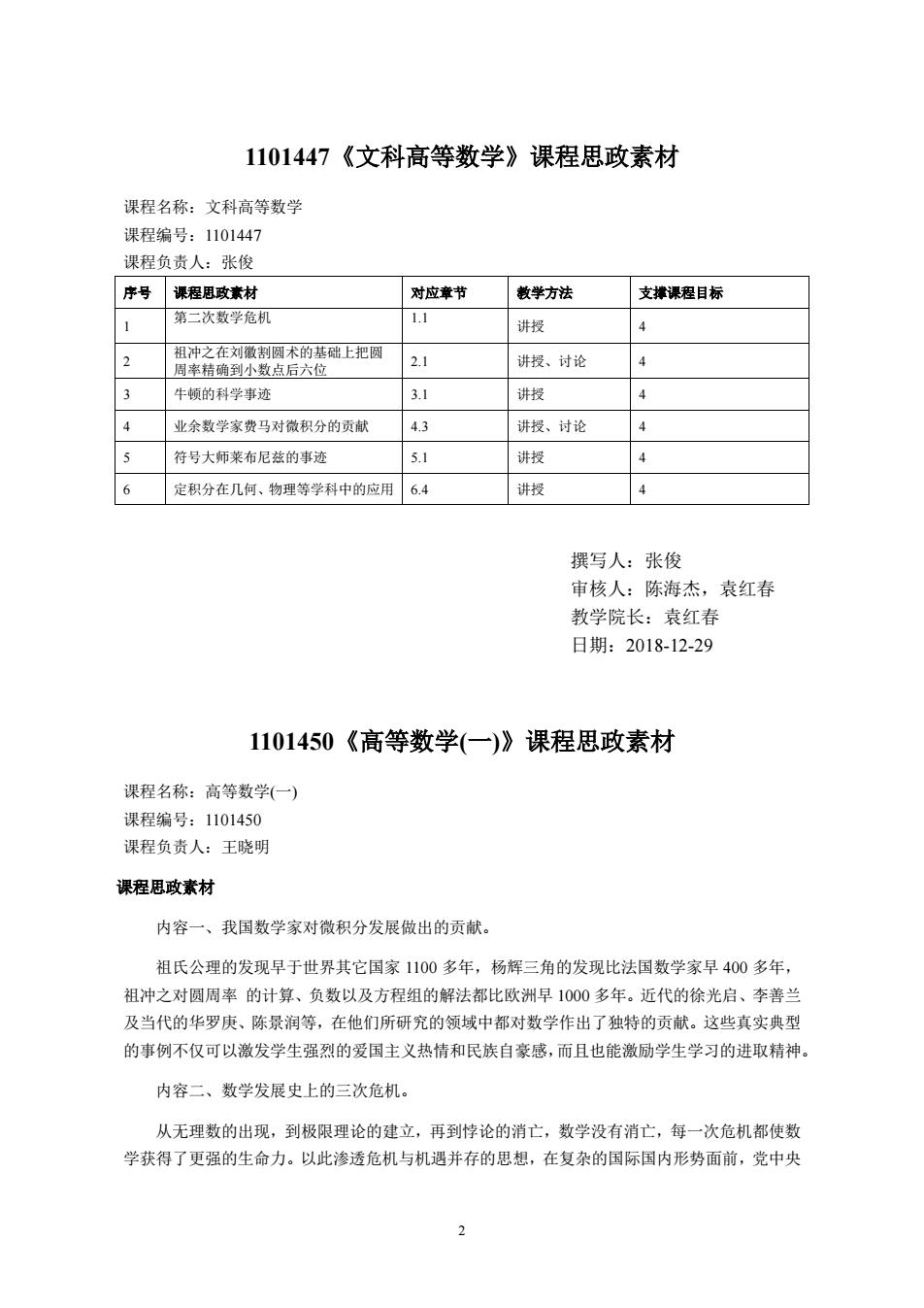
1101447《文科高等数学》课程思政素材 课程名称:文科高等数学 课程编号:1101447 课程负责人:张俊 序号课程思政素材 对应章节 敦学方法 支撑课程目标 第二次数学危机 讲授 2.1 讲授、讨论 牛倾的科学事迹 讲授 4 业余数学家数马对微积分的贡献 讲授、讨论 符号大师莱布尼兹的事迹 5.1 讲授 4 6 定积分在几何、物理等学科中的应用64 讲投 4 撰写人:张俊 审核人:陈海杰,袁红春 教学院长:袁红春 日期:2018-12-29 1101450《高等数学(一)》课程思政素材 课程名称:高等数学(一) 课程编号:1101450 课程负责人:王晓明 课程思政素材 内容一、我国数学家对微积分发展做出的贡献。 祖氏公理的发现早于世界其它国家1100多年,杨辉三角的发现比法国数学家早400多年, 祖冲之对圆周率的计算、负数以及方程组的解法都比欧洲早1000多年。近代的徐光启、李善兰 及当代的华罗庚、陈景润等,在他们所研究的领域中都对数学作出了独特的贡献。这些真实典型 的事例不仅可以激发学生强烈的爱国主义热情和民族自豪感,而且也能激励学生学习的进取精神 内容二、数学发展史上的三次危机。 从无理数的出现,到极限理论的建立,再到悖论的清亡,数学没有消亡,每一次危机都使数 学获得了更强的生命力。以此渗透危机与机遇并存的思想,在复杂的国际国内形势面前,党中央
2 1101447《文科高等数学》课程思政素材 课程名称:文科高等数学 课程编号:1101447 课程负责人:张俊 序号 课程思政素材 对应章节 教学方法 支撑课程目标 1 第二次数学危机 1.1 讲授 4 2 祖冲之在刘徽割圆术的基础上把圆 周率精确到小数点后六位 2.1 讲授、讨论 4 3 牛顿的科学事迹 3.1 讲授 4 4 业余数学家费马对微积分的贡献 4.3 讲授、讨论 4 5 符号大师莱布尼兹的事迹 5.1 讲授 4 6 定积分在几何、物理等学科中的应用 6.4 讲授 4 撰写人:张俊 审核人:陈海杰,袁红春 教学院长:袁红春 日期:2018-12-29 1101450《高等数学(一)》课程思政素材 课程名称:高等数学(一) 课程编号:1101450 课程负责人:王晓明 课程思政素材 内容一、我国数学家对微积分发展做出的贡献。 祖氏公理的发现早于世界其它国家 1100 多年,杨辉三角的发现比法国数学家早 400 多年, 祖冲之对圆周率 的计算、负数以及方程组的解法都比欧洲早 1000 多年。近代的徐光启、李善兰 及当代的华罗庚、陈景润等,在他们所研究的领域中都对数学作出了独特的贡献。这些真实典型 的事例不仅可以激发学生强烈的爱国主义热情和民族自豪感,而且也能激励学生学习的进取精神。 内容二、数学发展史上的三次危机。 从无理数的出现,到极限理论的建立,再到悖论的消亡,数学没有消亡,每一次危机都使数 学获得了更强的生命力。以此渗透危机与机遇并存的思想,在复杂的国际国内形势面前,党中央

国务院带领和团结全国各族人民,不动摇、不折腾、坚持科学发展观,聚精会神搞建设,一心一 意谋发展。我们会面临更多的挑战,各种不确定因素使得我们的前进道路更加曲折艰险,山穷水 复时我们不会丧失信心,柳暗花明中我们会看到更多的希望。 内容三、有限与无限、连续与间断、直线与曲线、近似与精确、微分和积分、收敛与发散、 未知与已知、相等与不等、常量与变量。 思格斯曾经指出:“现实世界的辩证法在数学概念和公式中能得到自己的反映,学生到处都 能遇到辩证法这些规律的表现。”例如,有限与无限、连续与间断、直线与曲线、近似与精确、 微分和积分、收敛与发散、未知与已知、相等与不等、常量与变量等。如我们在解某些系数中含 有字母的方程时,可视未知数为已知数,已知数为未知数:在处理含有参变数的问题时,参变数 既是变数,又是常数。刘微在割圆术中指出:随着圆内接正多边形边数的增加,它的周长和面积 越来越接近圆周长和圆面积。采用这种“化圆为方”、“化曲为直”的极限思想,通过观察“有限 分割”,想象“无限细分”,根据图形分割拼合的变化趋势想象它们的终极状态,不仅求出了圆的 周长,而且渗透了“变与不变”、“曲与直”、“近似与精确”、“有限与无限”、“量变与质变”等辩 证唯物主义思想。 内容四、数学符号化、数形结合 数学是一门既美又真的科学,数学美的主要特点是有序性、简明性、对称性和统一性。数学 命题从未知到已知的转化,充满了发现科学真理的喜悦。如符号化思想体现了简洁美,综合法与 分析法体现了有序美,数与形结合法体现了统一美,几何图形体现了对称美。在数学教学中,学 生获得数学的审美能力,既有利于激发学生对数学的兴趣,又有助于培养学生的创造能力。 内容五、数学应用、理论联系实际 数学应用的广泛性是数学学科的基本特征之一,加强数学与实际应用的联系已逐渐成为人们 的共识。近年来,高等数学的应用突破了过去狭隘的范畴,它与自然科学、社会科学、人文科学 相互渗透,在工农业生产、管理科学、医药卫生、计算机技术等领域发挥着显著的作用。此外, 高等数学与艺术也联系密切,如透视画与射影几何有关,音乐之声与傅立叶分析有关等。因此 高等数学教师在教学中,要体现数学来源于实际、寓于实际、用于实际的数学观,要树立构建数 学的学习观、在实践中学习数学的教学观,逐步培养学生理论联系实际的作风。 撰写人:王晓明 审核人:陈海杰,袁红春 教学院长:袁红春 日期:2018-11-23 3
3 国务院带领和团结全国各族人民,不动摇、不折腾、坚持科学发展观,聚精会神搞建设,一心一 意谋发展。我们会面临更多的挑战,各种不确定因素使得我们的前进道路更加曲折艰险,山穷水 复时我们不会丧失信心,柳暗花明中我们会看到更多的希望。 内容三、有限与无限、连续与间断、直线与曲线、近似与精确、微分和积分、收敛与发散、 未知与已知、相等与不等、常量与变量。 恩格斯曾经指出:“现实世界的辩证法在数学概念和公式中能得到自己的反映,学生到处都 能遇到辩证法这些规律的表现。”例如,有限与无限、连续与间断、直线与曲线、近似与精确、 微分和积分、收敛与发散、未知与已知、相等与不等、常量与变量等。如我们在解某些系数中含 有字母的方程时,可视未知数为已知数,已知数为未知数;在处理含有参变数的问题时,参变数 既是变数,又是常数。刘徽在割圆术中指出:随着圆内接正多边形边数的增加,它的周长和面积 越来越接近圆周长和圆面积。采用这种“化圆为方”、“化曲为直”的极限思想,通过观察“有限 分割”,想象“无限细分”,根据图形分割拼合的变化趋势想象它们的终极状态,不仅求出了圆的 周长,而且渗透了“变与不变”、“曲与直”、“近似与精确”、“有限与无限”、“量变与质变”等辩 证唯物主义思想。 内容四、数学符号化、数形结合 数学是一门既美又真的科学,数学美的主要特点是有序性、简明性、对称性和统一性。数学 命题从未知到已知的转化,充满了发现科学真理的喜悦。如符号化思想体现了简洁美,综合法与 分析法体现了有序美,数与形结合法体现了统一美,几何图形体现了对称美。在数学教学中,学 生获得数学的审美能力,既有利于激发学生对数学的兴趣,又有助于培养学生的创造能力。 内容五、数学应用、理论联系实际 数学应用的广泛性是数学学科的基本特征之一,加强数学与实际应用的联系已逐渐成为人们 的共识。近年来,高等数学的应用突破了过去狭隘的范畴,它与自然科学、社会科学、人文科学 相互渗透,在工农业生产、管理科学、医药卫生、计算机技术等领域发挥着显著的作用。此外, 高等数学与艺术也联系密切,如透视画与射影几何有关,音乐之声与傅立叶分析有关等。因此, 高等数学教师在教学中,要体现数学来源于实际、寓于实际、用于实际的数学观,要树立构建数 学的学习观、在实践中学习数学的教学观,逐步培养学生理论联系实际的作风。 撰写人:王晓明 审核人:陈海杰,袁红春 教学院长:袁红春 日期:2018-11-23