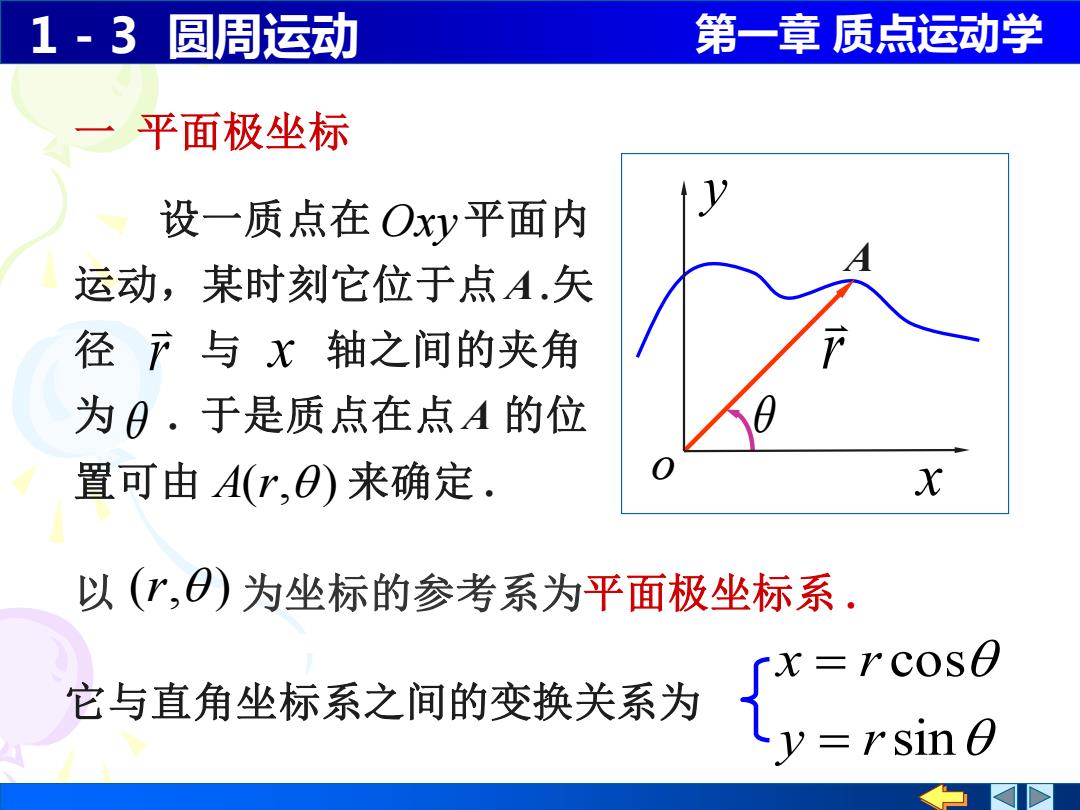
1-3圆周运动 第一章质点运动学 平面极坐标 设一质点在Oxy平面内 运动,某时刻它位于点A.矢 径产与x轴之间的夹角 为0.于是质点在点A的位 置可由A(r,O)来确定. X 以(“,)为坐标的参考系为平面极坐标系 ∫x=rcoso 它与直角坐标系之间的变换关系为 =rsin O
1 - 3 圆周运动 第一章 质点运动学 一 平面极坐标 A r x y o 设一质点在 平面内 运动,某时刻它位于点 A .矢 径 与 轴之间的夹角 为 . 于是质点在点 A 的位 置可由 A(r, ) 来确定 . Oxy r x 以 ) 为坐标的参考系为平面极坐标系 . (r, sin cos y r x r = = 它与直角坐标系之间的变换关系为
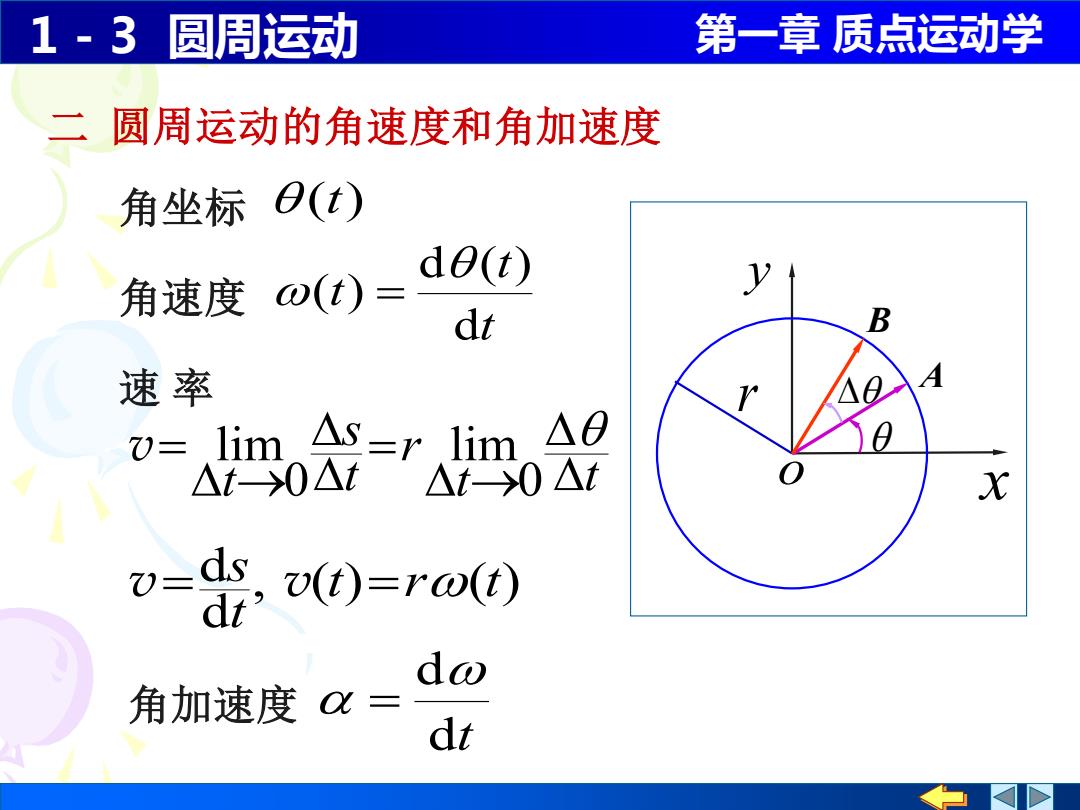
1-3圆周运动 第一章质点运动学 二 圆周运动的角速度和角加速度 角坐标B(t) dθ(t) 角速度ω(t)= dt 速率 lim As=r,lim,△8 △t-0△t△t0△t 器o0=ro0 dw 角加速度0三 dt
1 - 3 圆周运动 第一章 质点运动学 二 圆周运动的角速度和角加速度 t t t d d ( ) ( ) 角速度 = 角坐标 (t) 角加速度 dt d = 速 率 t t r t s t → = → = 0 lim 0 v lim x y o r , ( ) ( ) d d t r t t v= s v = A B
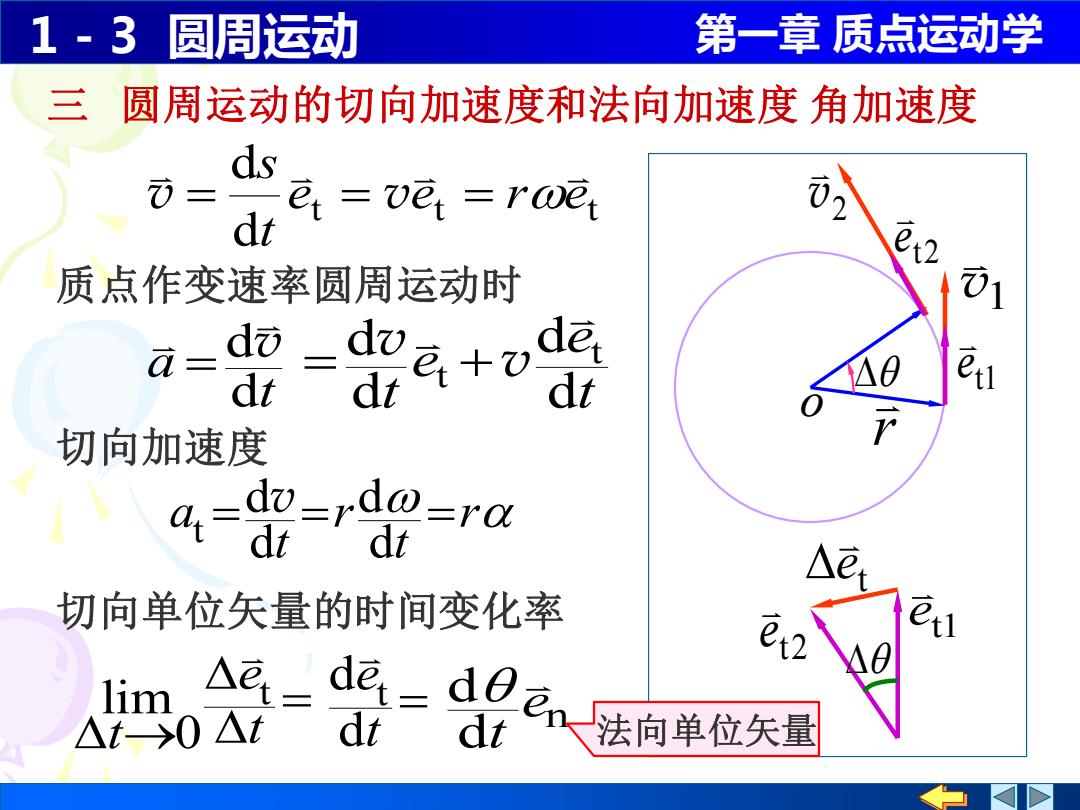
1-3圆周运动 第一章质点运动学 三 圆周运动的切向加速度和法向加速度角加速度 ds E=vt=rwe dt 质点作变速率圆周运动时 01 a- dò de dt dt dt △0 e 切向加速度 a-do-rdo-ra di △e, 切向单位矢量的时间变化率 lim A区二dE=Cn法向单位矢到 △t>0△t dt dt
1 - 3 圆周运动 第一章 质点运动学 v1 r o 三 圆周运动的切向加速度和法向加速度 角加速度 t e e t d d d d t t v v = + 2 v t t t d d e e r e t s v = = v = n d d e t t a d dv = r t r t a = = = d d d d t v 质点作变速率圆周运动时 t1 e t2 e 切向加速度 t1 e t2 e t e = → t e t t 0 lim 切向单位矢量的时间变化率 = t e d d t 法向单位矢量
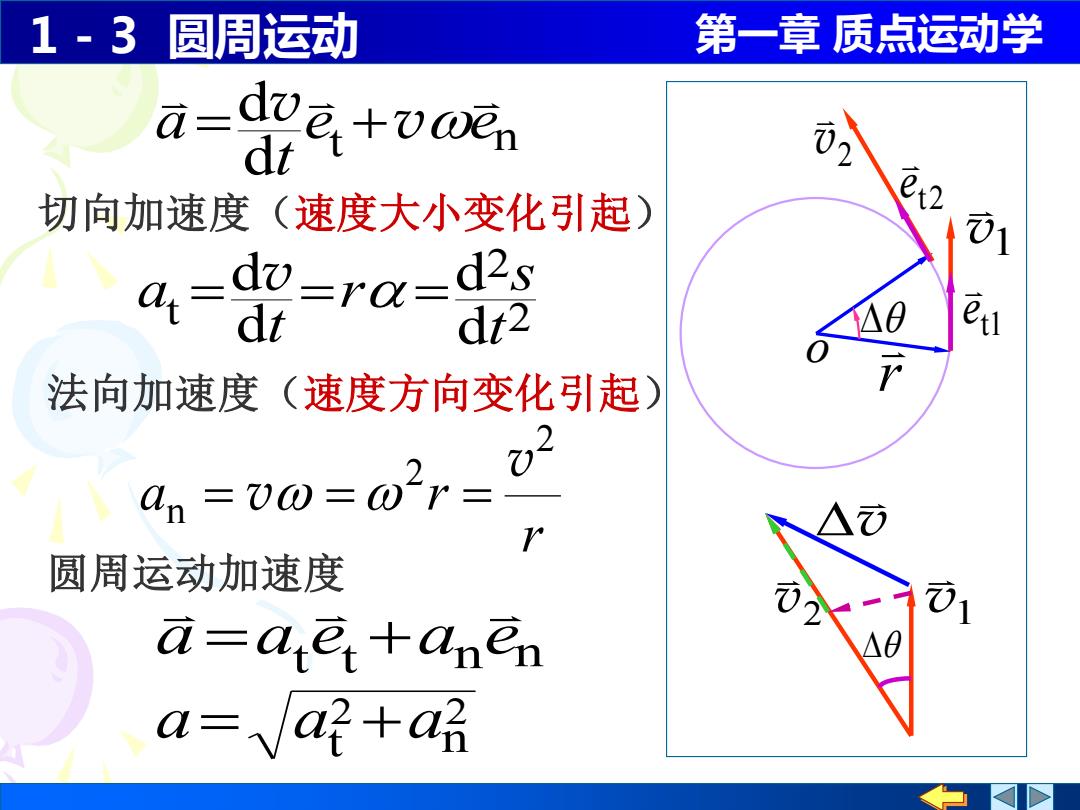
1-3圆周运动 第一章质点运动学 a-doe+vaen dt 切向加速度(速度大小变化引起) 01 a-do-ra- dr2 法向加速度(速度方向变化引起) an=v0=02r= 02 r 圆周运动加速度 a-ae +anen a=az+a
1 - 3 圆周运动 第一章 质点运动学 t n d d e e t a = v +v 切向加速度(速度大小变化引起) 2 2 t d d d d t s r t a = = = v 法向加速度(速度方向变化引起) r a r 2 2 n v = v = = a at et an en = + 圆周运动加速度 2 2 a= at +an v1 v2 v v1 r o 2 v t1 e t2 e
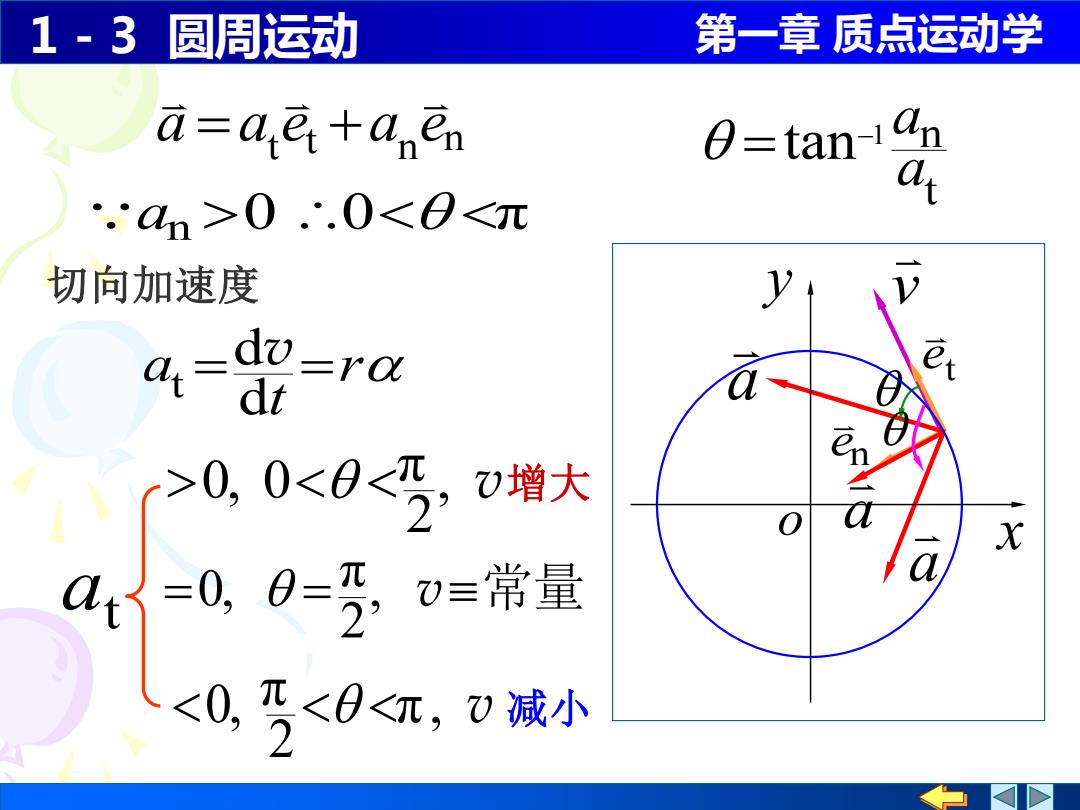
1-3圆周运动 第一章质点运动学 a-ae+a en 0=tan-ian .am>0.∴.0<0<元 切向加速度 dt =r0 >0,0<6<, )增大 X t =0,0=,。 =常量 <0, <0<,0诚小
1 - 3 圆周运动 第一章 质点运动学 v 切向加速度 r t a = = d d t v at π , v 2 π 0, 减小 , v 增大 2 π 0, 0 = = , v常量 2 π 0, t e en a a a t 1 n tan a − a = an 0 0 π x y o a at et a n en = +