
2 5牛顿定律的应用举例 第二章牛顿定律 解题的基本思路 1)确定研究对象进行受力分析; (隔离物体,画受力图) 2)取坐标系; 3)列方程(一般用分量式); 4)利用其它的约束条件列补充方程; 5)先用文字符号求解,后带入数据计算结果
2 – 5 牛顿定律的应用举例 第二章 牛顿定律 1)确定研究对象进行受力分析; (隔离物体,画受力图) 2)取坐标系; 3)列方程(一般用分量式); 4)利用其它的约束条件列补充方程; 5)先用文字符号求解,后带入数据计算结果. 解题的基本思路
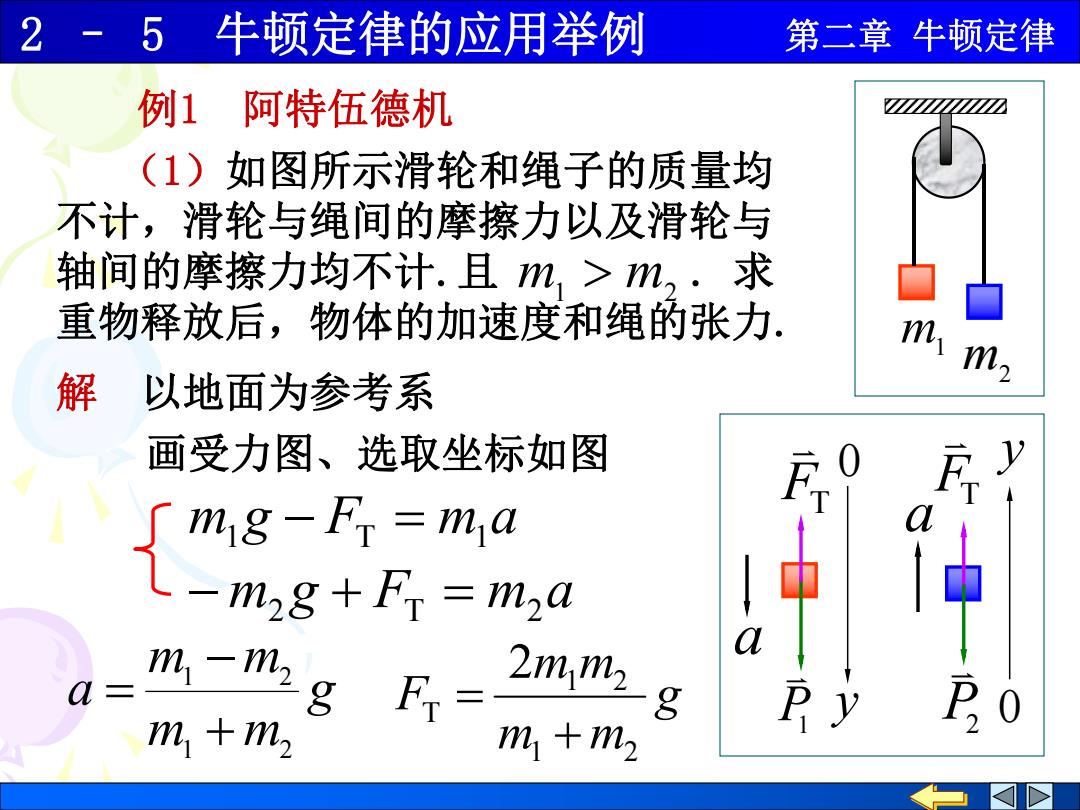
2-5牛顿定律的应用举例 第二章牛顿定律 例1阿特伍德机 z☑ (1)如图所示滑轮和绳子的质量均 不计,滑轮与绳间的摩擦力以及滑轮与 轴间的摩擦力均不计.且m,>m,.求 重物释放后,物体的加速度和绳的张力 m m 解 以地面为参考系 画受力图、选取坐标如图 mg-Fr=ma a zmg+FT=ma 中 a= 2mmzg a m1+m2 m +m Py
2 – 5 牛顿定律的应用举例 第二章 牛顿定律 P1 FT (1)如图所示滑轮和绳子的质量均 不计,滑轮与绳间的摩擦力以及滑轮与 轴间的摩擦力均不计.且 . 求 重物释放后,物体的加速度和绳的张力. m1 m2 m1 m2 m1g FT m1a m2 g FT m2a g m m m m a 1 2 1 2 g m m m m F 1 2 1 2 T 2 解 以地面为参考系 画受力图、选取坐标如图 FTP2 a y 0 a y 0 例1 阿特伍德机

2-5牛顿定律的应用举例 第二章牛顿定律 (2)若将此装置置于电梯顶部,当 电梯以加速度相对地面向上运动时, 求两物体相对电梯的加速度和绳的张力. a 解以地面为参考系 0 a 设两物体相对于地面的加速度分别 m m2 为d、a2,且相对电梯的加速度为a, mg-Fr=ma i一(g+a) F a-a-a m1+m2 m2g+F=4,(F= 2mmz (g+a) a,=a,+a m +m Py
2 – 5 牛顿定律的应用举例 第二章 牛顿定律 P1 FT (2)若将此装置置于电梯顶部,当 电梯以加速度 相对地面向上运动时, 求两物体相对电梯的加速度和绳的张力. a m1 m2 a r a r a 解 以地面为参考系 设两物体相对于地面的加速度分别 为 、 ,且相对电梯的加速度为 1 a ar 2 a FTP2 1 a y 0 a2 y 0 m1g FT m1a1 2 T 2 2 m g F m a a a a 1 r a2 ar a ( ) 1 2 1 2 r g a m m m m a ( ) 2 1 2 1 2 T g a m m m m F
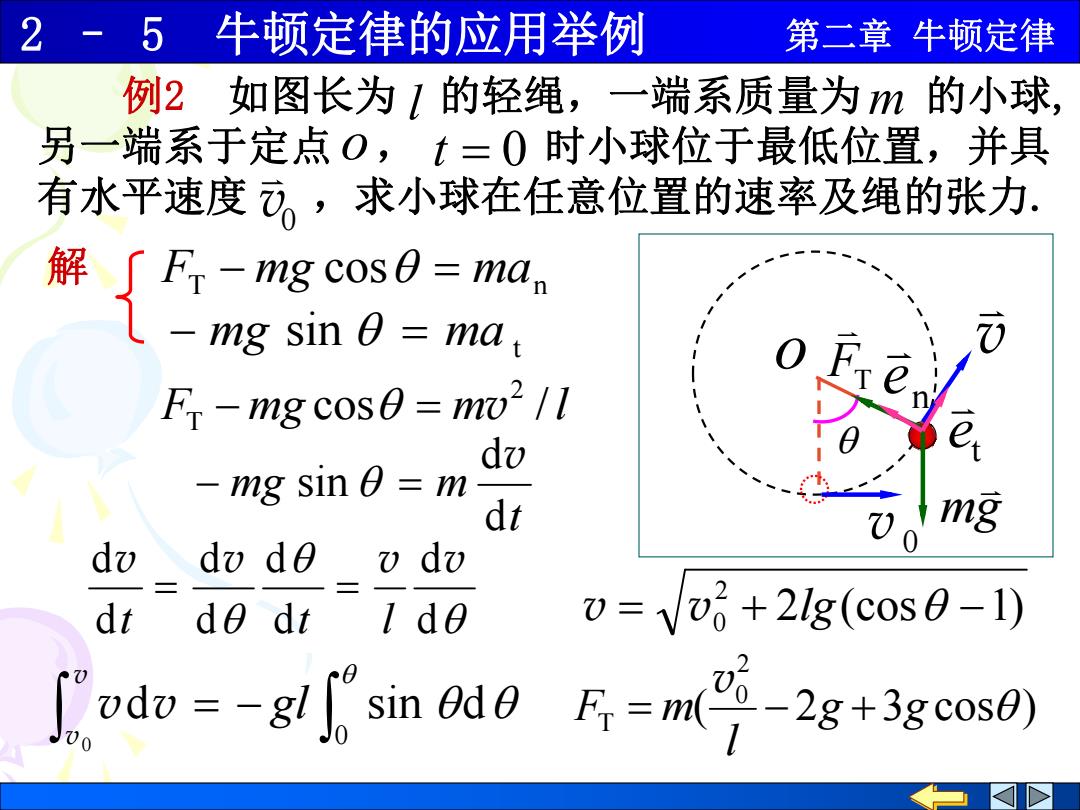
2-5牛顿定律的应用举例 第二章牛顿定律 例2如图长为1的轻绳,一端系质量为m的小球, 另一端系于定点0,t=0时小球位于最低位置,并具 有水平速度。,求小球在任意位置的速率及绳的张力. mg coso nia -mg sin 0 ma, Fr-mg cos0 =mu2/1 dv -mg sin =m dt mg dv do de v dv dt do dt 1d0 )=V+2lg(cos日-1) dsin adm-28+3cos0)
2 – 5 牛顿定律的应用举例 第二章 牛顿定律 t mg m d d sin v 解 0 d sin d 0 gl v v v v ( 2 3 cos ) 2 0 T g g l F m v d d d d d d d dv v v v t t l 2 (cos 1) 2 v v0 lg t mg sin ma T n F mg cos ma F mg cos m / l 2 T v 例2 如图长为 的轻绳,一端系质量为 的小球, 另一端系于定点 , 时小球位于最低位置,并具 有水平速度 ,求小球在任意位置的速率及绳的张力. 0 v m t 0 l o o v 0 v FT mg t e n e

2 -5牛顿定律的应用举例 第二章牛顿定律 例3如图所示(圆锥摆),长为1的细绳一端固 定在天花板上,另一端悬挂质量为m的小球,小球经 推动后,在水平面内绕通过圆心O的铅直轴作角速度 为ω的匀速率圆周运动.问绳和铅直方向所成的角 度日为多少?空气阻力不计. 解F+p=ma ) (F sine=map =m=mro T FT COS0-P=0 r =Isin0
2 – 5 牛顿定律的应用举例 第二章 牛顿定律 例3 如图所示(圆锥摆),长为 的细绳一端固 定在天花板上,另一端悬挂质量为 的小球,小球经 推动后,在水平面内绕通过圆心 的铅直轴作角速度 为 的匀速率圆周运动 . 问绳和铅直方向所成的角 度 为多少?空气阻力不计. m l o o l r v A n e t e 解 F P ma T 2 2 T n sin mr r F ma m v FT cos P 0 r lsin FT P