
§1.4体积功 一、{ 体积功:W=-心pdV 二、可逆过程 三、相变体积功 16
16 一、体积功: §1.4 体积功 二、可逆过程 三、相变体积功 2 1 V V W p = − 外dV
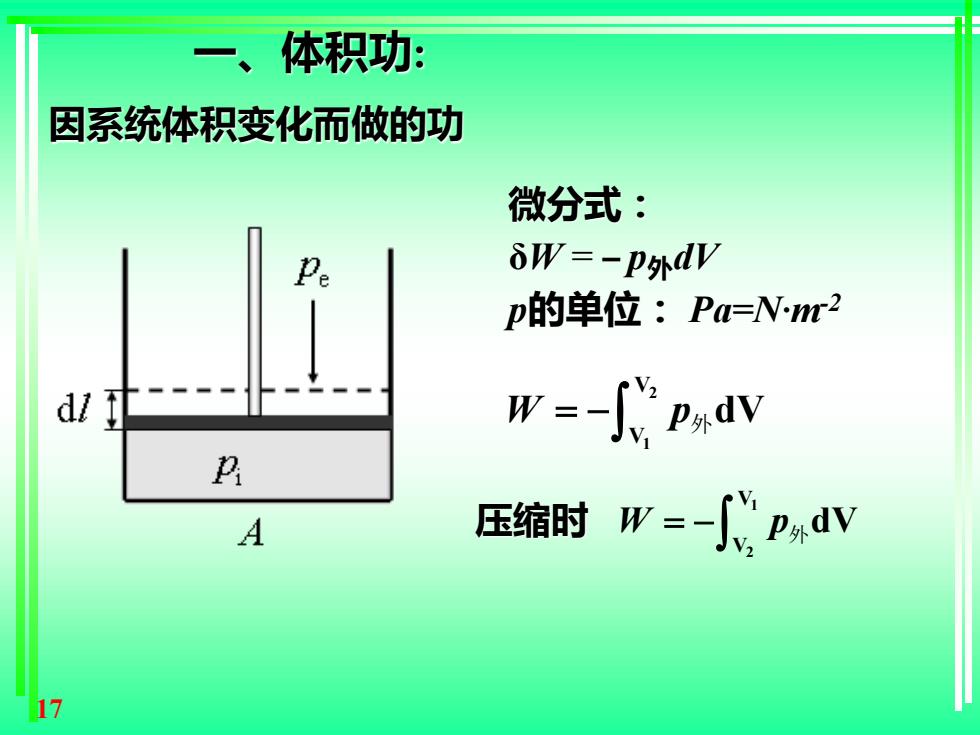
一、体积功: 因系统体积变化而做的功 微分式: Pe δW=-p外dV p的单位:Pa=Nm2 dl w=-心pdv P A 压缩时W=-心PdV 17
17 一、体积功: 因系统体积变化而做的功 微分式: δW = – p外dV p的单位: Pa=N·m-2 压缩时 2 1 V V W p = − 外dV1 2 V V W p = − 外dV

设在定温下,一定量理想气体在活塞筒中克服外压 Pe,经4种不同途径,体积从V膨胀到所作的功。 (1)向真空自由膨胀: Pe-0 W1=0 18
18 ⑴ 向真空自由膨胀: W1=0 设在定温下,一定量理想气体在活塞筒中克服外压 pe ,经4种不同途径,体积从V1膨胀到V2所作的功。 pe=0
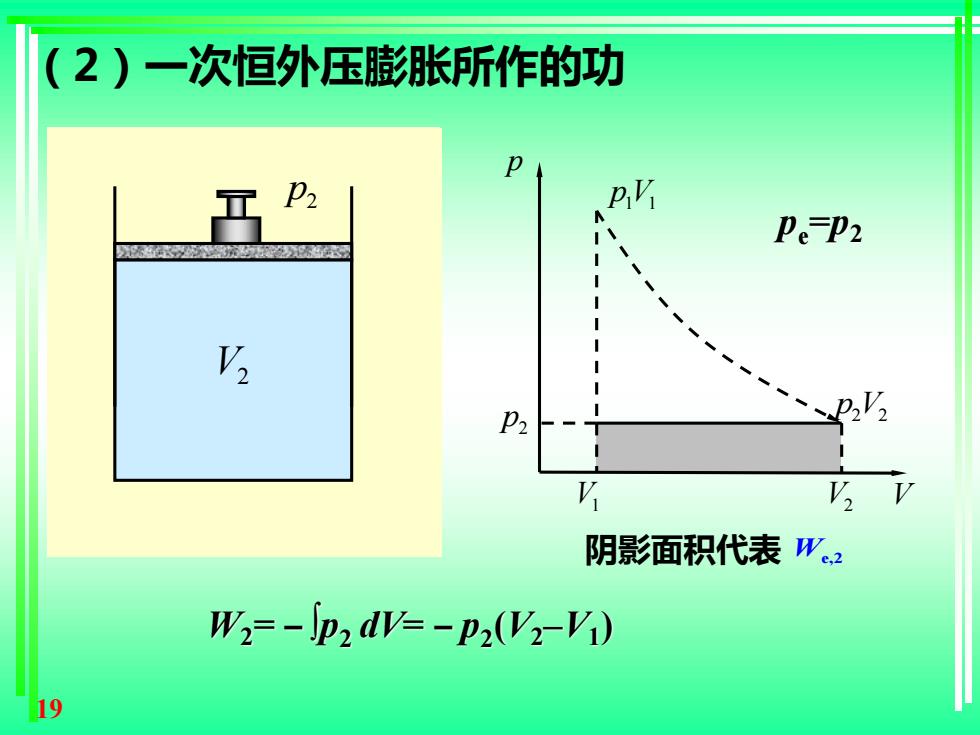
(2)一次恒外压膨胀所作的功 Pe-p2 P2 阴影面积代表 We2 W2=-p2dW-p2(V-1) 19
19 V1 1 p pV1 1 p2 V1 V2 V p p V2 2 2 p V1 V2 p2 (2)一次恒外压膨胀所作的功 阴影面积代表 We,2 W2= – ∫p2 dV= – p2 (V2–V1 ) pe =p2
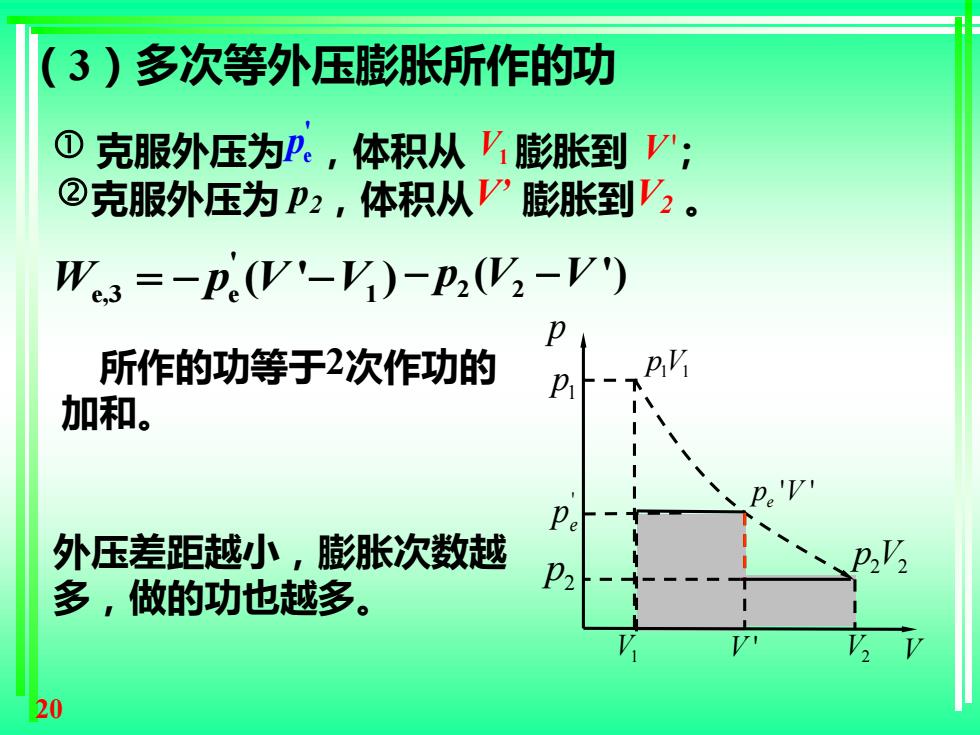
(3)多次等外压膨胀所作的功 O克服外压为P。,体积从膨胀到V; ②克服外压为P2,体积从V膨胀到V,。 W3=-p(V'-V)-P2(W2-V) P 所作的功等于2次作功的 加和。 10 外压差距越小,膨胀次数越 多,做的功也越多。 20
20 外压差距越小,膨胀次数越 多,做的功也越多。 所作的功等于2次作功的 加和。 1 1 pV V p 2 2 p V 1 p ' e p V ' ' ' e p V 2 p V1 V2 e,3 e 1 ' W p V V = − − ( ' ) 克服外压为 e ,体积从 V1 膨胀到 V ; ' ' p 2 2 − − p V V ( ') 克服外压为 p2,体积从V’ 膨胀到V2 。 (3)多次等外压膨胀所作的功