
AABAAACAAAAD (⊙)单支树改造后完全二叉树的顺序存储状态 图6.6右单支二叉树及其顺序存储示意图 二叉树的顺序存储表示可描述为: #define MAXNODE /体二又树的最大结点数*制 typedef elemtype SqBiTree[MAXNODE] /0号单元存放根结点/ SqBiTree bt; 即将bt定义为含有MAXNODE个elemtype类型元素的一维数组。 2.链式存储结构 所谓二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示着元素的 逻辑关系。通常有下面两种形式。 (1)二叉链表存储 链表中每个结点由三个域组成,除了数据域外,还有两个指针域,分别用来给出该结 点左孩子和右孩子所在的链结点的存储地址。结点的存储的结构为: Ichild data rchild 其中,d血ta域存放某结点的数据信息:1 lchild与rchild分别存放指向左孩子和右孩 子的指针,当左孩子或右孩子不存在时,相应指针域值为空(用符号∧或NLL表示)。 图6.7(a)给出了图6.36)所示的一棵二叉树的二叉链表示。 二叉链表也可以带头结点的方式存放,如图6.7)所示。 头指针bt 头结点指针bt A A AD、 AEAAFAADAEAAFA AGA (回带头指针的二叉链表 ⑥)带头结点的二叉链表 图6.7图6.3b)所示二叉树的二叉链表表示示意图 108
108 A ∧ B ∧ ∧ ∧ C ∧ ∧ ∧ ∧ ∧ ∧ ∧ D (c) 单支树改造后完全二叉树的顺序存储状态 图 6.6 右单支二叉树及其顺序存储示意图 二叉树的顺序存储表示可描述为: #define MAXNODE /*二叉树的最大结点数*/ typedef elemtype SqBiTree[MAXNODE] /*0 号单元存放根结点*/ SqBiTree bt; 即将 bt 定义为含有 MAXNODE 个 elemtype 类型元素的一维数组。 2.链式存储结构 所谓二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示着元素的 逻辑关系。通常有下面两种形式。 (1)二叉链表存储 链表中每个结点由三个域组成,除了数据域外,还有两个指针域,分别用来给出该结 点左孩子和右孩子所在的链结点的存储地址。结点的存储的结构为: 其中,data 域存放某结点的数据信息;lchild 与 rchild 分别存放指向左孩子和右孩 子的指针,当左孩子或右孩子不存在时,相应指针域值为空(用符号∧或 NULL 表示)。 图 6.7(a)给出了图 6.3(b)所示的一棵二叉树的二叉链表示。 二叉链表也可以带头结点的方式存放,如图 6.7(b)所示。 头指针 bt 头结点指针 bt (a) 带头指针的二叉链表 (b) 带头结点的二叉链表 图 6.7 图 6.3(b)所示二叉树的二叉链表表示示意图 lchild data rchild A B ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ A C D E F D E F B C G ∧ G ∧
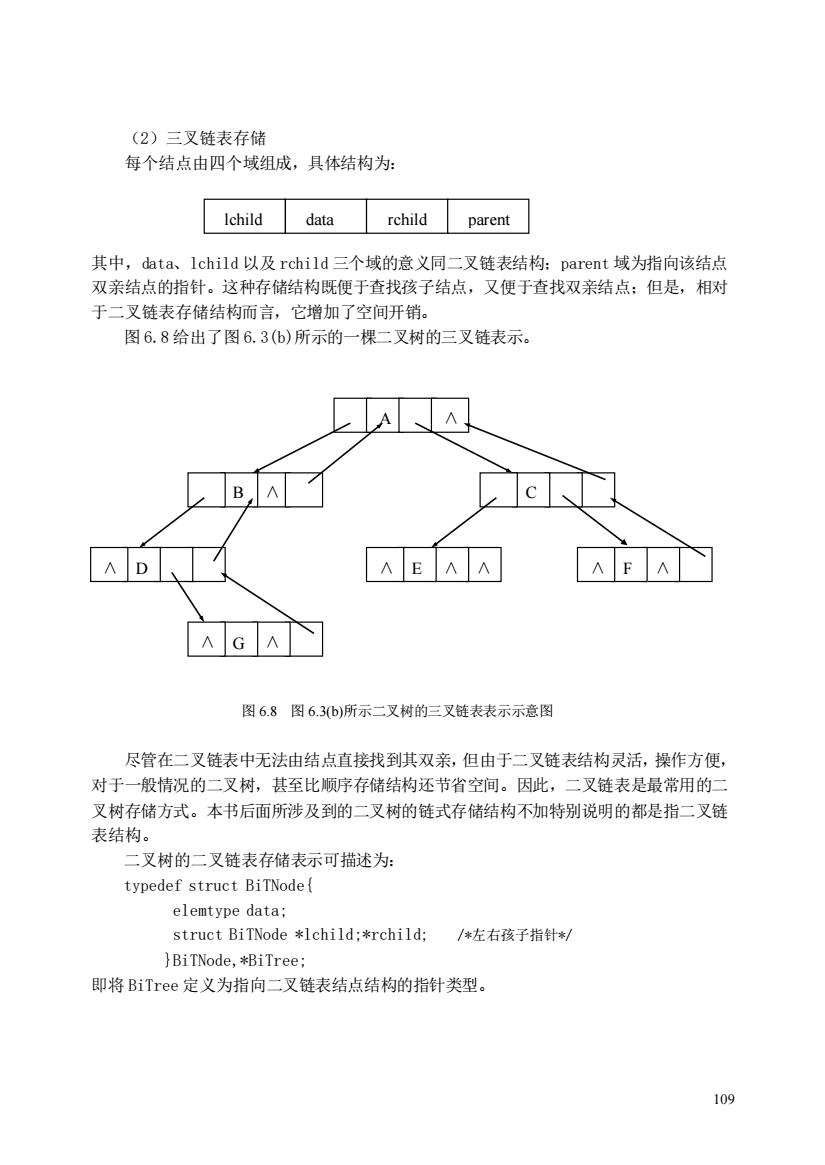
(2)三叉链表存储 每个结点由四个域组成,具体结构为: Ichild data rchild parent 其中,data、lchild以及rchild三个域的意义同二叉又链表结构:parent域为指向该结点 双亲结点的指针。这种存储结构既便于查找孩子结点,又便于查找双亲结点:但是,相对 于二叉链表存储结构而言,它增加了空间开销。 图6.8给出了图6.3(6)所示的一棵二叉树的三叉链表示。 A D AEAA AFA AGA 图6.8图6.3b)所示二叉树的三叉链表表示示意图 尽管在二叉链表中无法由结点直接找到其双亲,但由于二叉链表结构灵活,操作方便, 对于一般情况的二叉树,甚至比顺序存储结构还节省空间。因此,二叉链表是最常用的二 叉树存储方式。本书后面所涉及到的二叉树的链式存储结构不加特别说明的都是指二叉链 表结构。 二叉树的二叉链表存储表示可描述为: typedef struct BiTNode( elemtype data: struct BiTNode*1child:*rchild;/左右孩子指针*/ }BiTNode,*BiTree: 即将BiTree定义为指向二叉链表结点结构的指针类型。 109
109 (2)三叉链表存储 每个结点由四个域组成,具体结构为: 其中,data、lchild 以及 rchild 三个域的意义同二叉链表结构;parent 域为指向该结点 双亲结点的指针。这种存储结构既便于查找孩子结点,又便于查找双亲结点;但是,相对 于二叉链表存储结构而言,它增加了空间开销。 图 6.8 给出了图 6.3(b)所示的一棵二叉树的三叉链表示。 图 6.8 图 6.3(b)所示二叉树的三叉链表表示示意图 尽管在二叉链表中无法由结点直接找到其双亲,但由于二叉链表结构灵活,操作方便, 对于一般情况的二叉树,甚至比顺序存储结构还节省空间。因此,二叉链表是最常用的二 叉树存储方式。本书后面所涉及到的二叉树的链式存储结构不加特别说明的都是指二叉链 表结构。 二叉树的二叉链表存储表示可描述为: typedef struct BiTNode{ elemtype data; struct BiTNode *lchild;*rchild; /*左右孩子指针*/ }BiTNode,*BiTree; 即将 BiTree 定义为指向二叉链表结点结构的指针类型。 lchild data rchild parent A ∧ B ∧ ∧ D ∧ E ∧ ∧ C ∧ F ∧ ∧ G ∧

6.2.2二叉树的基本操作及实现 1,二叉树的基本操作 二叉树的基本操作通常有以下几种: (I)Initiate(bt)建立一棵空二叉树。 (2)Creae(x,It,rbt)生成一棵以x为根结点的数据域信息,以二叉树bt和rb 为左子树和右子树的二叉树。 (3)InsertL(bt,x,parent)将数据域信息为x的结点插入到二叉树bt中作为结点 parent的左孩子结点。如果结点parent原来有左孩子结点,则将结点parent原来的左孩子 结点作为结点x的左孩子结点。 (4)InsertR(bt,x,parent)将数据域信息为x的结点插入到二叉树bt中作为结点 parent的右孩子结点。如果结点parent原来有右孩子结点,则将结点parent原来的右孩子 结点作为结点x的右孩子结点。 (S)DeleteL(bt,parent)在二叉树bt中除结点parent的左子树 (6)DeleteR(bt,parent)在二叉树bt中别除结点parent的右子树。 (7)Search(bt,x)在二叉树bt中查找数据元素x。 (8)Traverse(bt)按某种方式遍历二叉树bt的全部结点。 2.算法的实现 算法的实现依赖于具体的存储结构,当二叉树采用不同的存储结构时,上述各种操作 的实现算法是不同的。下面讨论基于二叉链表存储结构的上述操作的实现算法。 (1)Initiate(bt)初始建立二叉树bt,并使bt指向头结点。在二叉树根结点前建立头 结点,就如同在单链表前建立的头结点,可以方便后边的一些操作实现 int Initiate (BiTree *bt) {初始化建立二叉树bt的头结点* if((*bt=(BiTNode*)malloc(sizeof(BiTNode)-NULL) return0: *ht->lchild=NJ几I *bt->rchild=NULL: return上 算法6.1 110
110 6.2.2 二叉树的基本操作及实现 1.二叉树的基本操作 二叉树的基本操作通常有以下几种: (1)Initiate(bt)建立一棵空二叉树。 (2)Create(x,lbt,rbt)生成一棵以 x 为根结点的数据域信息,以二叉树 lbt 和 rbt 为左子树和右子树的二叉树。 (3)InsertL(bt,x,parent)将数据域信息为 x 的结点插入到二叉树 bt 中作为结点 parent 的左孩子结点。如果结点 parent 原来有左孩子结点,则将结点 parent 原来的左孩子 结点作为结点 x 的左孩子结点。 (4)InsertR(bt,x,parent)将数据域信息为 x 的结点插入到二叉树 bt 中作为结点 parent 的右孩子结点。如果结点 parent 原来有右孩子结点,则将结点 parent 原来的右孩子 结点作为结点 x 的右孩子结点。 (5)DeleteL(bt,parent)在二叉树 bt 中删除结点 parent 的左子树。 (6)DeleteR(bt,parent)在二叉树 bt 中删除结点 parent 的右子树。 (7)Search(bt,x)在二叉树 bt 中查找数据元素 x。 (8)Traverse(bt)按某种方式遍历二叉树 bt 的全部结点。 2.算法的实现 算法的实现依赖于具体的存储结构,当二叉树采用不同的存储结构时,上述各种操作 的实现算法是不同的。下面讨论基于二叉链表存储结构的上述操作的实现算法。 (1)Initiate(bt)初始建立二叉树 bt,并使 bt指向头结点。在二叉树根结点前建立头 结点,就如同在单链表前建立的头结点,可以方便后边的一些操作实现。 int Initiate (BiTree *bt) {/*初始化建立二叉树*bt 的头结点*/ if((*bt=(BiTNode *)malloc(sizeof(BiTNode)))==NULL) return 0; *bt->lchild=NULL; *bt->rchild=NULL; return 1; } 算法 6.1

(2)Creae(x,t,rbt)建立一棵以x为根结点的数据域信息,以二叉树Ibt和rbt 为左右子树的二叉树。建立成功时返回所建二叉树结点的指针:建立失败时返回空指针。 BiTree Create (elemtype x,BiTree lbt,BiTree rbt) {作生成一棵以x为根结点的数据域值以b和t为左右子树的二叉树*/ BiTree p: if((p-(BiTNode+)malloc(sizeof(BiTNode)))=-NULL)return NULL p->data=x, p->Ichild=Ibt p->rchild=rbt: return p. 算法6.2 (3)InsertL (b,x,parent) BiTree InsertL (BiTree bt,elemtype x,BiTree parent) {产在二叉树bt的结点parent的左子树插入结点数据元素x BiTree p: if(parent-NULL) {printf("n插入出错": return NULL; if((p=(BiTNode*)malloc(sizeof(BiTNode)))=-NULL)return NULL; p->data=x: p->rchild=NULL: if(parent->Ichild-NULL)parent->lchild=p; else p->Ichild=parent->child; parent->Ichild=p; return bt; 算法6.3 (4)InsertR(bt,X,parent)功能类同于(3),算法略。 (S)DeleteL(bt,parent)在二叉树bt中删除结点parent的左子树。当parent或parent 的左孩子结点为空时删除失败。别除成功时返回根结点指针:删除失败时返回空指针。 BiTree DeleteL (BiTree bt,BiTree parent) {/在二叉树bt中刷除结点parent的左子树/ BiTree P. 111
111 (2)Create(x,lbt,rbt)建立一棵以 x 为根结点的数据域信息,以二叉树 lbt 和 rbt 为左右子树的二叉树。建立成功时返回所建二叉树结点的指针;建立失败时返回空指针。 BiTree Create(elemtype x,BiTree lbt,BiTree rbt) {/*生成一棵以x 为根结点的数据域值以 lbt 和 rbt 为左右子树的二叉树*/ BiTree p; if ((p=(BiTNode *)malloc(sizeof(BiTNode)))==NULL) return NULL; p->data=x; p->lchild=lbt; p->rchild=rbt; return p; } 算法 6.2 (3)InsertL(bt,x,parent) BiTree InsertL(BiTree bt,elemtype x,BiTree parent) {/*在二叉树 bt 的结点 parent 的左子树插入结点数据元素 x*/ BiTree p; if (parent==NULL) { printf(“\n 插入出错”); return NULL; } if ((p=(BiTNode *)malloc(sizeof(BiTNode)))==NULL) return NULL; p->data=x; p->lchild=NULL; p->rchild=NULL; if (parent->lchild==NULL) parent->lchild=p; else {p->lchild=parent->lchild; parent->lchild=p; } return bt; } 算法 6.3 (4)InsertR(bt,x,parent)功能类同于(3),算法略。 (5)DeleteL(bt,parent)在二叉树 bt 中删除结点 parent 的左子树。当parent 或parent 的左孩子结点为空时删除失败。删除成功时返回根结点指针;删除失败时返回空指针。 BiTree DeleteL(BiTree bt,BiTree parent) {/*在二叉树 bt 中删除结点 parent 的左子树*/ BiTree p;

if(parent-=NULLJparent->Ichild-NULL) {printf("n删除出错"): return NULL' p=parent->Ichild; parent->lchild=NULL: fce(p以当p为叶子结点时,这样删除仅释放了所子树根结点的空间,/ 小若要别除子树分支中的结点,需用后面介绍的遍历操作来实现。/ return br, 算法6.4 (6)DeleteR(bt,parent)功能类同于(S),只是除结点parent的右子树。算法略 操作Search(bt,x)实际是遍历操作Traverse(bt)的特例,关于二叉树的遍历操作 的实现,将在下一节中重点介绍。 6.3二叉树的遍历 6.3.1二叉树的遍历方法及递归实现 二叉树的遍历是指按照某种顺序访问二叉树中的每个结点,使每个结点被访问一次且 仅被访问一次。 遍历是二叉树中经常要用到的一种操作。因为在实际应用问题中,常常需要按一定顺 序对二叉树中的每个结点逐个进行访问,查找具有某一特点的结点,然后对这些满足条件 的结点进行处理。 通过一次完整的遍历,可使二叉树中结点信息由非线性排列变为某种意义上的线性序 列。也就是说,遍历操作使非线性结构线性化。 由二叉树的定义可知,一 棵由根结点、根结点的左子树和根结点的右子树三部分组成。 因此,只要依次遍历这三部分,就可以遍历整个二叉树。若以D、L、R分别表示访问根 结点、遍历根结点的左子树、遍历根结点的右子树,则二叉树的遍历方式有六种:DLR、 LDR、LRD、DRL、RDL和RLD。如果限定先左后右,则只有前三种方式,即DLR(称 为先序遍历)、LDR(称为中序遍历)和LRD(称为后序遍历)。 112
112 if (parent==NULL||parent->lchild==NULL) { printf(“\n 删除出错”); return NULL’ } p=parent->lchild; parent->lchild=NULL; free(p); /*当 p 为非叶子结点时,这样删除仅释放了所删子树根结点的空间,*/ /*若要删除子树分支中的结点,需用后面介绍的遍历操作来实现。*/ return br; } 算法 6.4 (6)DeleteR(bt,parent)功能类同于(5),只是删除结点 parent 的右子树。算法略。 操作 Search(bt,x)实际是遍历操作 Traverse(bt)的特例,关于二叉树的遍历操作 的实现,将在下一节中重点介绍。 6.3 二叉树的遍历 6.3.1 二叉树的遍历方法及递归实现 二叉树的遍历是指按照某种顺序访问二叉树中的每个结点,使每个结点被访问一次且 仅被访问一次。 遍历是二叉树中经常要用到的一种操作。因为在实际应用问题中,常常需要按一定顺 序对二叉树中的每个结点逐个进行访问,查找具有某一特点的结点,然后对这些满足条件 的结点进行处理。 通过一次完整的遍历,可使二叉树中结点信息由非线性排列变为某种意义上的线性序 列。也就是说,遍历操作使非线性结构线性化。 由二叉树的定义可知,一棵由根结点、根结点的左子树和根结点的右子树三部分组成。 因此,只要依次遍历这三部分,就可以遍历整个二叉树。若以 D、L、R 分别表示访问根 结点、遍历根结点的左子树、遍历根结点的右子树,则二叉树的遍历方式有六种:DLR、 LDR、LRD、DRL、RDL 和 RLD。如果限定先左后右,则只有前三种方式,即 DLR(称 为先序遍历)、LDR(称为中序遍历)和 LRD(称为后序遍历)