
第五章树 树是一类重要的非线性数据结构,是以分支关 系定义的层次结构 §5.1树的定义 ★定义 定义:树(tree)是n(n>O)个结点的有限集T,其中: ●有且仅有一个特定的结点,称为树的根(【00) ●当n>1时,其余结点可分为m(m>0)个互不相交的有限集 T1,T2,.Tm,其中每一个集合本身又是一棵树,称为根的 子树(subtree) 必特点: ●树中至少有一个结点—根 ●树中各子树是互不相交的集合
第五章 树 树是一类重要的非线性数据结构,是以分支关 系定义的层次结构 §5.1 树的定义 定义 ❖定义:树(tree)是n(n>0)个结点的有限集T,其中: ⚫有且仅有一个特定的结点,称为树的根(root) ⚫当n>1时,其余结点可分为m(m>0)个互不相交的有限集 T1,T2,.Tm,其中每一个集合本身又是一棵树,称为根的 子树(subtree) ❖特点: ⚫树中至少有一个结点——根 ⚫树中各子树是互不相交的集合
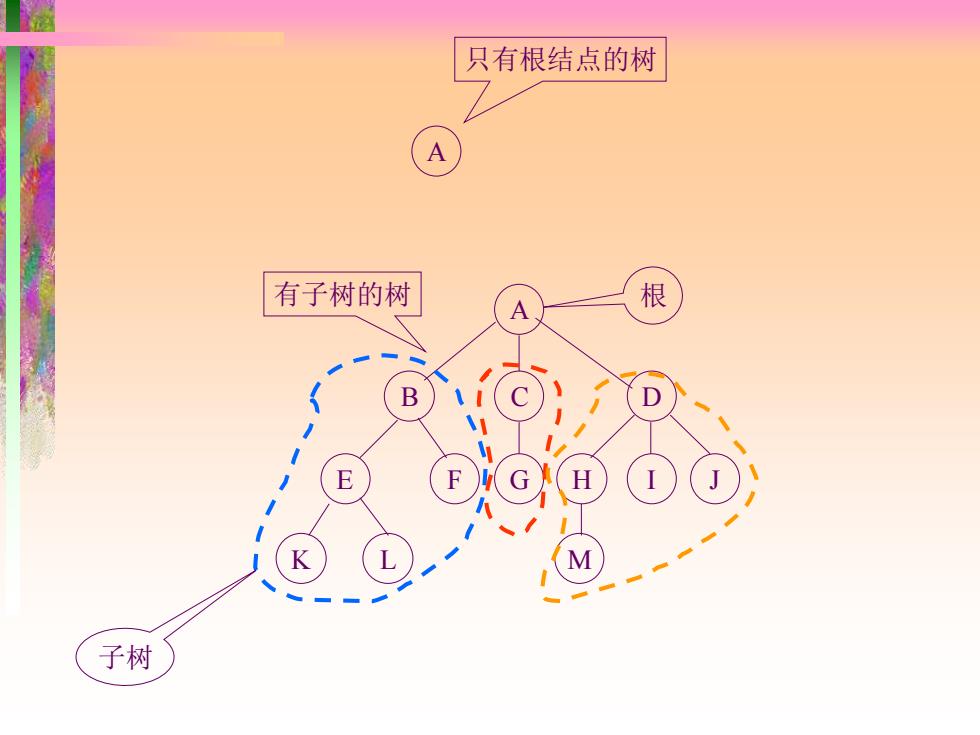
只有根结点的树 有子树的树 根 子树
A 只有根结点的树 A B C D E F G H I J K L M 有子树的树 根 子树

★基本术语 结点(n0d)一表示树中的元素,包括数据项及若干 指向其子树的分支 结点的度(degree) 一结点拥有的子树数 叶子(leaf)一度为0的结点 冬孩子(child一结点子树的根称为该结点的孩子 双亲(parents)—孩子结点的上层结点叫该结点的~ 冬兄弟(sibling)一J同一双亲的孩子 必树的度 棵树中最大的结点度数 冬结点的层次(level)一从根结点算起, 根为第一层, 它的孩子为第二层 必深度(depth)—树中结点的最大层次数 森林(forest)—m(m≥0)棵互不相交的树的集合
基本术语 ❖结点(node)——表示树中的元素,包括数据项及若干 指向其子树的分支 ❖结点的度(degree)——结点拥有的子树数 ❖叶子(leaf)——度为0的结点 ❖孩子(child)——结点子树的根称为该结点的孩子 ❖双亲(parents)——孩子结点的上层结点叫该结点的~ ❖兄弟(sibling)——同一双亲的孩子 ❖树的度——一棵树中最大的结点度数 ❖结点的层次(level)——从根结点算起,根为第一层, 它的孩子为第二层. ❖深度(depth)——树中结点的最大层次数 ❖森林(forest)——m(m0)棵互不相交的树的集合

结点A的度:3 叶子:K,L,F,G,M,I,J 结点B的度:2 结点M的度:O 结点I的双亲:D 结点A的孩子:B,C,D 结点L的双亲:E 结点B的孩子:E,F 结点B,C,D为兄弟 B 树的度:3 结点K,L为兄弟 E 树的深度:4 结点A的层次:1 结点F,G为堂兄弟 结点M的层次:4 结点A是结点F,G的祖先
A B C D E F G H I J K L M 结点A的度:3 结点B的度:2 结点M的度:0 叶子:K,L,F,G,M,I,J 结点A的孩子:B,C,D 结点B的孩子:E,F 结点I的双亲:D 结点L的双亲:E 结点B,C,D为兄弟 树的度:3 结点K,L为兄弟 结点A的层次:1 结点M的层次:4 树的深度:4 结点F,G为堂兄弟 结点A是结点F,G的祖先
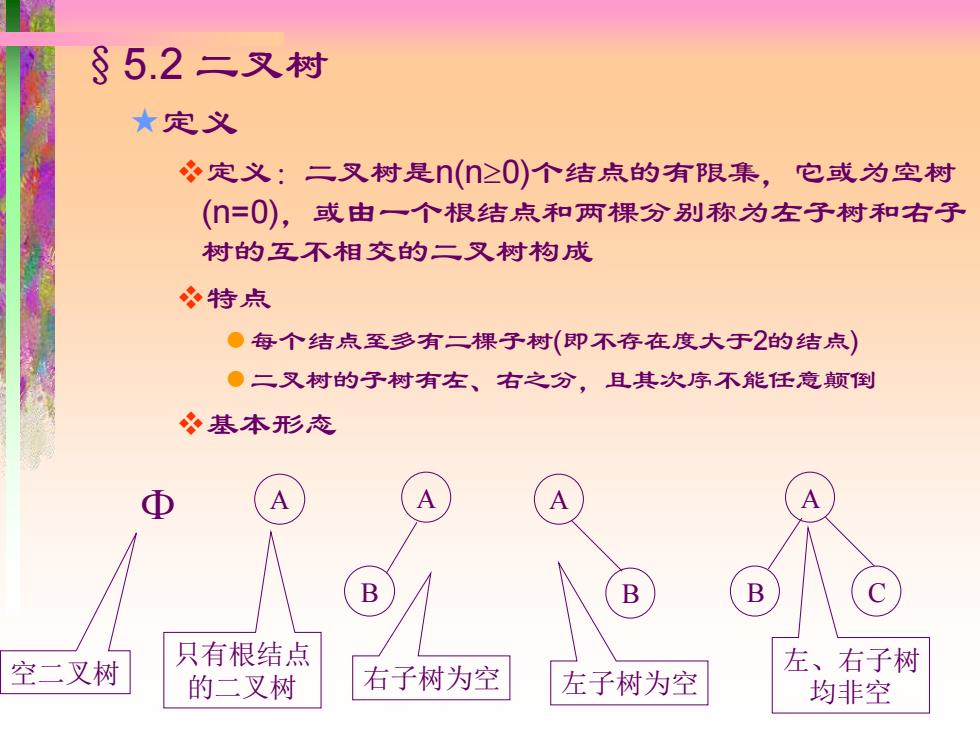
§5.2二叉树 ★定义 冬定义:二叉树是n(≥0)个结点的有限集,它或为空树 (=0),或由一个根结点和两棵分别称为左子树和右子 树的互不相交的二叉树构成 冬特点 ●每个结点至多有二棵子树(即不存在度大于2的结点) ●二叉树的子树有左、右之分,且其次序不能任意颠倒 基本形态 A B B 空二叉树 只有根结点 左、右子树 的二叉树 右子树为空 左子树为空 均非空
§5.2 二叉树 定义 ❖定义:二叉树是n(n0)个结点的有限集,它或为空树 (n=0),或由一个根结点和两棵分别称为左子树和右子 树的互不相交的二叉树构成 ❖特点 ⚫每个结点至多有二棵子树(即不存在度大于2的结点) ⚫二叉树的子树有左、右之分,且其次序不能任意颠倒 ❖基本形态 A 只有根结点 的二叉树 空二叉树 A B 右子树为空 A B 左子树为空 A B C 左、右子树 均非空