
11-2-1概念映射(U—一>AC) 从输入空间U至概念(虚拟)存储器AC的映射。 n维输入向量:"p=[41p,2p,…,np] 量化编码为[u。],之后映射至AC的c个存储单元,即被u,】激活的单元 (c为二进非零单元的数目),映射后的向量(0次接收域函数),见图: R。=S([up])=[s,(up]),2(Iup]),…,s.(up])] s,(u,])=1 j=1,2,…c 映射原则:输入空间邻近两点(一点为一个输入n维向量),在AC中 有部分重叠单元被激励。距离越近,重叠越多;距离远的点,在AC中 不重叠,称局域泛化,C一一泛化常数。 AC 杂散编码 ● 输入向量 AP(W) c=4 输出 (a) 一维c=4 U输入空间 图2-7-1CMAC结构
11-2-1 概念映射(U——>AC) 从输入空间 U 至概念(虚拟)存储器 AC 的映射。 n 维输入向量: u p p p np T [u , u , , u ] 1 2 量化编码为 [u ] p ,之后映射至 AC 的 c 个存储单元,即被 [u ] p 激活的单元 (c 为二进非零单元的数目),映射后的向量(0 次接收域函数),见图: R p u p u p u p c u p T S ([ ]) [s ([ ]),s ([ ]), ,s ([ ])] 1 2 s j c j p ([u ]) 1 , 1,2, 映射原则:输入空间邻近两点(一点为一个输入 n 维向量),在 AC 中 有部分重叠单元被激励。距离越近,重叠越多;距离远的点,在 AC 中 不重叠,称局域泛化,c——泛化常数。 (a) 一维 c=4 1 c=4 y AC + U输入空间 杂散编码 AP(W) 输出 输入向量 图2-7-1 CMAC结构

11-2-2实际映射(Ac一>Ap) 由AC的c个单元,用杂散编码(压缩存储空间)技术,映射至 实际存储器AP的c个单元(存着相应权值),网络输出,为AP中 c个单元权值和。设单输出: y,=∑",s,uD=Rw,wn=w1,w2L,wL,w' 将S(u,])=1代入有 wj 经两次映射: 相近的输入,产生相近的输出: 不同的输入,产生不同的输出
11-2-2 实际映射(AC——>AP)
11-2-3.杂散存储 ·若输入是n维,年一维有q个量化级,则AC占很大容量。但是,训 练样本不可能遍历所有输入空间,在C中被激励的单元是很稀疏 的。 ·杂散存储:可将AC压缩到较小的AP中。 有多种方法,“除余数法”是其中较好的一种。 杂散存储弱点:产生碰撞(冲突)即AC中多个联想单元,被映射到 AR的同一单元(见图这意味着信息、的丢失。 (b)邻近两点输入重叠单元=3,无碰撞 (c)邻近两点输入重叠单元=3,有碰撞 那么CMAC是怎样实貌上述各种映射的?碰撞的原因? 下面通过一个具体示例来说明(见板书)
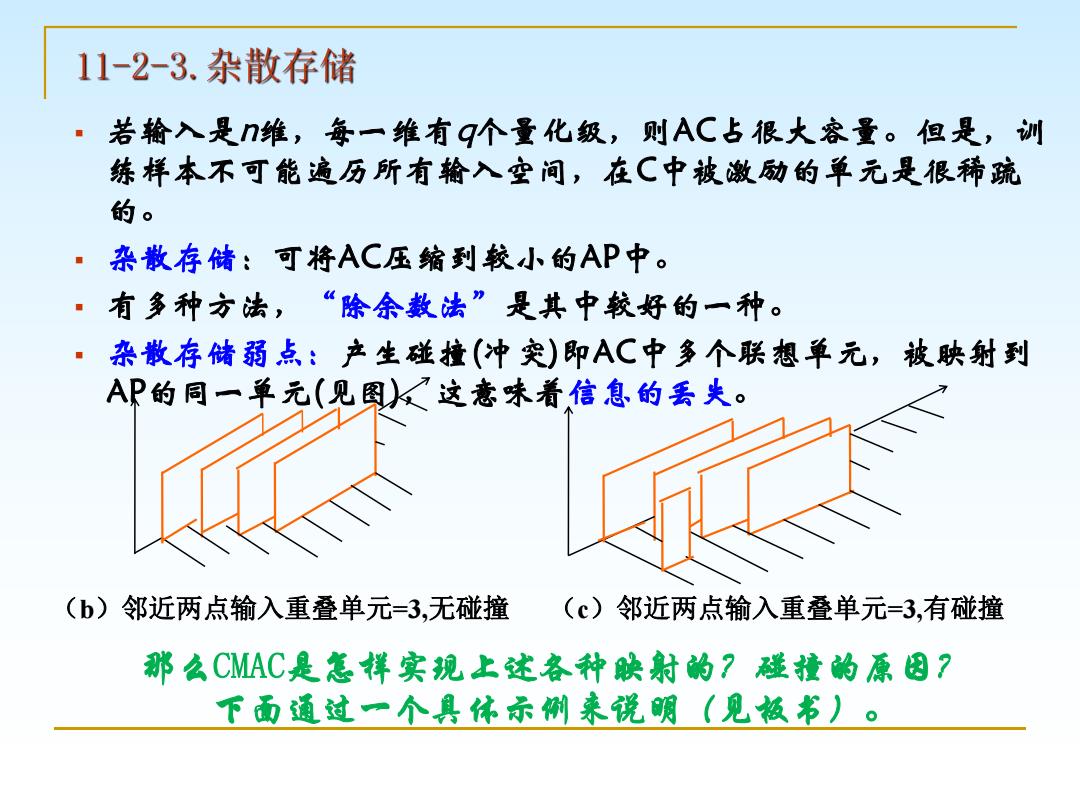
§ 若输入是n维,每一维有q个量化级,则AC占很大容量。但是,训 练样本不可能遍历所有输入空间,在C中被激励的单元是很稀疏 的。 § 杂散存储:可将AC压缩到较小的AP中。 § 有多种方法, “除余数法”是其中较好的一种。 § 杂散存储弱点:产生碰撞(冲突)即AC中多个联想单元,被映射到 AP的同一单元(见图),这意味着信息的丢失。 (b)邻近两点输入重叠单元=3,无碰撞 (c)邻近两点输入重叠单元=3,有碰撞 那么CMAC是怎样实现上述各种映射的?碰撞的原因? 下面通过一个具体示例来说明(见板书)

11-3CMAC算法及程序语言描述 113-1学习算法 CMAC 为有导师的学习算法。 设单输出,给定输入/输出样本对(导师信号):up/dp, p=1,2,…,L 由ò规则调整权值: Aw,(0=nd。-y》suD I 其中 lRp2=∑su)=c 将Rp代入得 △w,(t)=n ,-y(a》=n0 可见:c个单元权值的调整量是相同的
11-3 CMAC算法及程序语言描述 CMAC 为有导师的学习算法。 设单输出,给定输入 /输出样本对 (导师信号 ):u P d p / , p 1,2,, L 。 由d 规则调整权值: Dw t d y t s j p p j p P ( ) ( ( )) ([ ]) - h u R 2 其中 R P j u j c p s c 2 2 1 å ([ ]) 将 2 R P 代入得 Dw t d y t c e t c j p p p ( ) ( ( )) ( ) - h h 可见 :c 个单元权值的调整量是相同的

11-3CMAC算法及程序语言描述 11-3-2学习算法分析 CMAC的学习算法与自适应线性神经元的相同。但,因有 重叠、碰撞,故对学习算法及收敛性,需予以分析(讨论 单输出)。 ▣ 分析算法 Gauss-Seidel迭代法; Jacobij迭代法 分析情况、结论 (1)输入样本有重叠, 杂散编码无碰撞 若重叠少,解收敛 (2)输入样本有重叠,杂散编码有碰撞 因碰撞,收敛速度降低、收敛性态变坏、也可能不收敛
CMAC的学习算法与自适应线性神经元的相同。但,因有 重叠、碰撞,故对学习算法及收敛性,需予以分析(讨论 单输出)。 q 分析算法 Gauss-Seidel迭代法; Jacobi迭代法 q 分析情况、结论 (1) 输入样本有重叠,杂散编码无碰撞 若重叠少,解收敛 (2) 输入样本有重叠,杂散编码有碰撞 因碰撞,收敛速度降低、收敛性态变坏、也可能不收敛 11-3 CMAC算法及程序语言描述