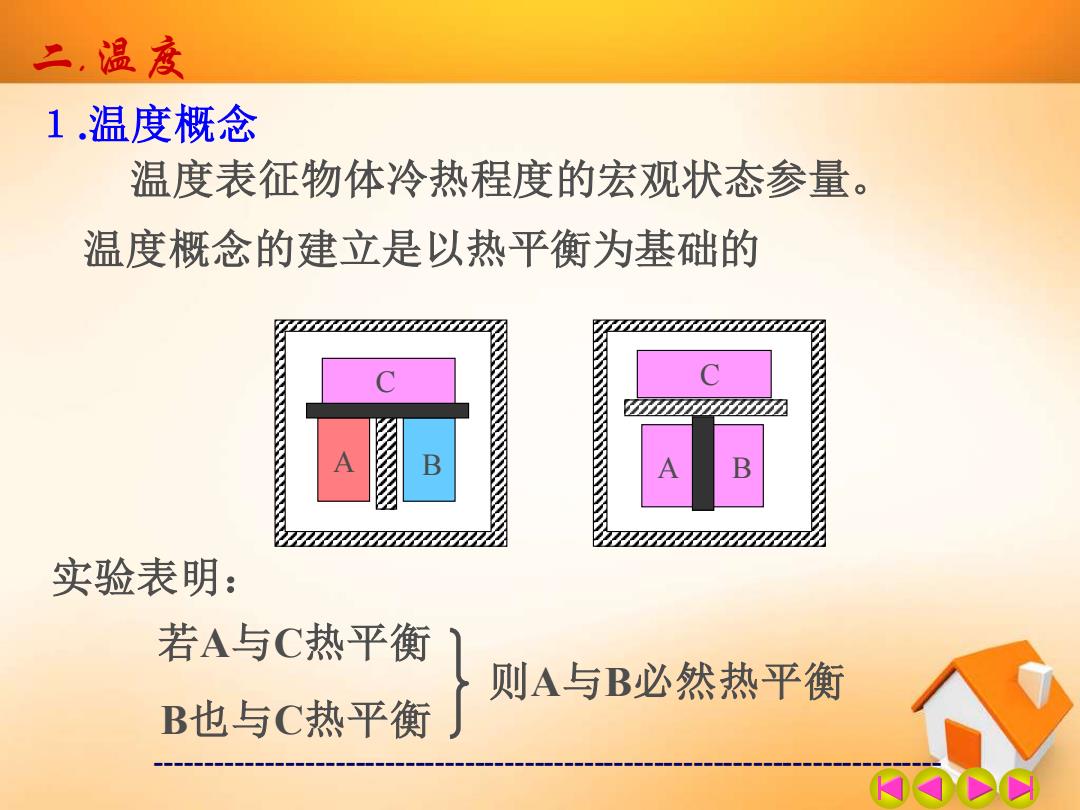
二,温度 1.温度概念 温度表征物体冷热程度的宏观状态参量。 温度概念的建立是以热平衡为基础的 实验表明: 若A与C热平衡 则A与B必然热平衡 B也与C热平衡
------------------------------------------------------------------------------- 二.温度 1.温度概念 温度表征物体冷热程度的宏观状态参量。 温度概念的建立是以热平衡为基础的 A B C A B C 实验表明: 若A与C热平衡 B也与C热平衡 则A与B必然热平衡

热力学第零定律: 如果两个系统分别与第三个系统达到热平衡,那 么,这两个系统彼此也处于热平衡。(热平衡定律) 热平衡定律说明,处在相互热平衡状态的系统必 定拥有某一个共同的宏观物理性质。 定义:处在相互热平衡状态的系统所具有的共同的 宏观性质叫温度。 ·一切处于同一热平衡态的系统有相同的温度 2.温标 温度的数值表示法。 摄氏温标、热力学温标 T=t+273.15
------------------------------------------------------------------------------- 热力学第零定律: 如果两个系统分别与第三个系统达到热平衡,那 么,这两个系统彼此也处于热平衡。 (热平衡定律)。 热平衡定律说明,处在相互热平衡状态的系统必 定拥有某一个共同的宏观物理性质。 定义: 处在相互热平衡状态的系统所具有的共同的 宏观性质叫温度。 • 一切处于同一热平衡态的系统有相同的温度 2.温标 温度的数值表示法。 摄氏温标、热力学温标 T = t + 273.15

三.理想气体状态方程 M pV= RT M 克拉珀龙方程 Mmol为气体的摩尔质量; M为气体的质量; R为普适气体常量,R=8.31(J/mo1·K1): 平衡态还常用状态图中的一个点来表示 D一V图、p一T图、V一T图) PA(PLViTi) B(P2,V2,T2) 0 V K
------------------------------------------------------------------------------- 三.理想气体状态方程 RT M M pV mol = 克拉珀龙方程 Mmol为气体的摩尔质量; M为气体的质量; R为普适气体常量,R=8.31(J/mol-1﹒K-1 ); •平衡态还常用状态图中的一个点来表示 (p-V图、p-T图、V-T图) p V 0 A(p1 ,V1 ,T1 ) B(p2 ,V2 ,T2 )

§5.2理想气体的压强和温度 一、理想气体分子模型和统计假设 1.理想气体的分子模型: ()分子可以看作质点。 (2)除碰撞外,分子力可以略去不计。 (3)分子间的碰撞是完全弹性的 理想气体的分子模型是弹性的自由运动的质点。 2平衡态时,理想气体分子的统计假设有: (1)无外场时,气体分子在各处出现的概率相同。 分子的数密度n处处相同, (2)由于碰撞,分子可以有各种不同的速度,速度 取向各方向等概率。 2=D=_足=D2=b2
------------------------------------------------------------------------------- §5.2 理想气体的压强和温度 一、理想气体分子模型和统计假设 1.理想气体的分子模型: (1) 分子可以看作质点。 (2) 除碰撞外,分子力可以略去不计。 (3) 分子间的碰撞是完全弹性的。 理想气体的分子模型是弹性的自由运动的质点。 2.平衡态时,理想气体分子的统计假设有: (1) 无外场时,气体分子在各处出现的概率相同。 分子的数密度n处处相同, (2) 由于碰撞,分子可以有各种不同的速度,速度 取向各方向等概率。 2 2 2 x = y = z x = y = z
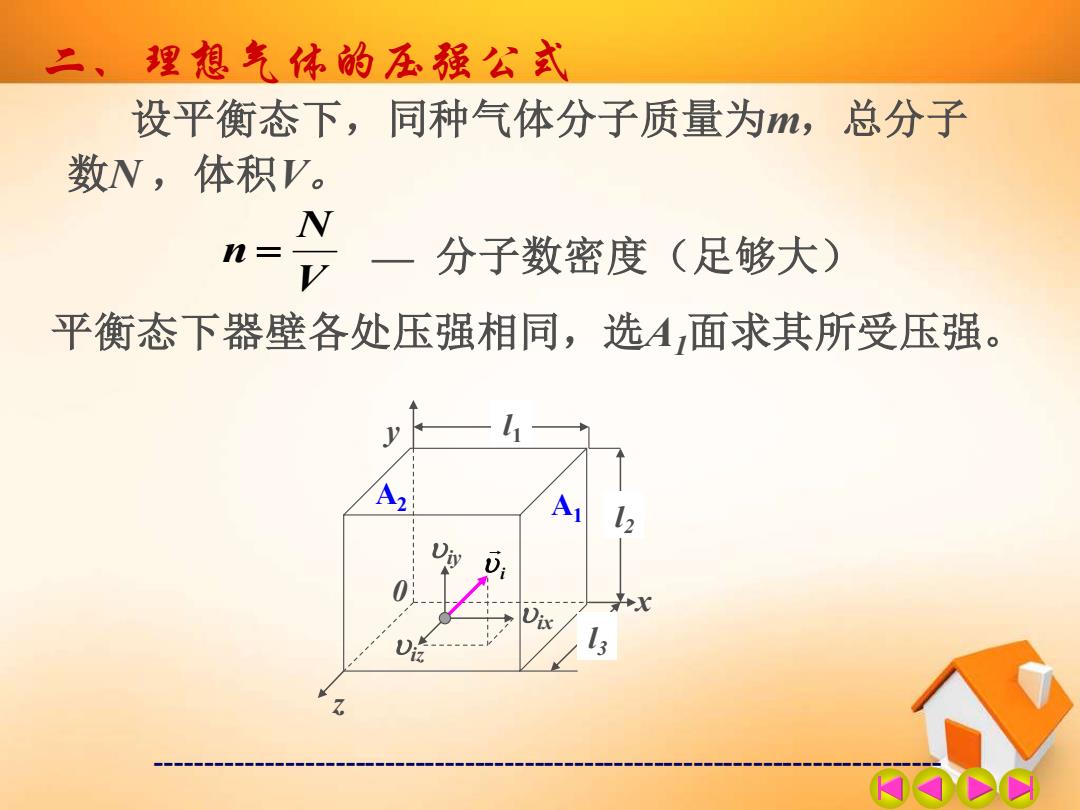
二、理想气体的压强公式 设平衡态下,同种气体分子质量为m,总分子 数N,体积V。 N n= V 一分子数密度(足够大) 平衡态下器壁各处压强相同,选A面求其所受压强。 12 13
------------------------------------------------------------------------------- 二、理想气体的压强公式 设平衡态下,同种气体分子质量为m,总分子 数N ,体积V。 V N n = — 分子数密度(足够大) 平衡态下器壁各处压强相同,选A1面求其所受压强。 iz z x y 0 ix iy A1 A2 l3 l2 l1 i