
第12卷第5期 智能系统学报 Vol.12 No.5 2017年10月 CAAI Transactions on Intelligent Systems 0ct.2017 D0I:10.11992/is.201612026 网络出版地址:http:/kns.cmki.net/kcms/detail/23.1538.TP.20170s08.0922.004.html 一种增强局部搜索能力的改进人工蜂群算法 刘晓芳,柳培忠,骆炎民,范宇凌 (1.华侨大学工学院,福建泉州362021:2.华侨大学计算机科学与技术学院,福建厦门361021) 摘要:针对人工蜂群算法初始化群体分布不均匀和局部搜索能力弱的问题,本文提出了一种增强局部搜索能力的 人工蜂群算法(SABC)。首先,在种群初始化阶段采用高维洛伦兹混沌系统,得到遍历性好、有规律的初始群体,避 免了随机初始化的盲目性。然后,采用基于对数函数的适应度评价方式,以增大种群个体间差异,减小选择压力,避 免过早收敛。最后,在微分进化算法的启发下,提出了一种新的搜索策略,采用当前种群中的最佳个体来引导下一 代的更新,以提高算法的局部搜索能力。通过对12个经典测试函数的仿真实验,并与其他经典的改进人工蜂群算法 对比,结果表明:本文算法具有良好的寻优性能,无论在解的精度还是收敛速度方面效果都有所提高。 关键词:人工蜂群算法:高维混沌系统:适应度评价:搜索策略:优化算法:演化算法:收敛性分析:精度分析:智能 算法 中图分类号:TP18文献标志码:A文章编号:1673-4785(2017)05-0684-10 中文引用格式:刘晓芳,柳培忠,骆炎民,等.一种增强局部搜索能力的改进人工蜂群算法[J].智能系统学报,2017,12(5): 684-693. 英文引用格式:LIU Xiaofang,LIU Peizhong,LUO Yanmin,ctal.Improved artificial bee colony algorithm based on enhanced local search[J].CAAI transactions on intelligent systems,2017,12(5):684-693. Improved artificial bee colony algorithm based on enhanced local search LIU Xiaofang',LIU Peizhong',LUO Yanmin2,FAN Yuling' (1.Engineering school,Huaqiao University,Quanzhou 362021,China;2.School of Computer Science and Technology,Huaqiao University,Xiamen 361021,China) Abstract:The shortcomings of the artificial bee colony algorithm (ABC)are its uneven initial population distribution and weak local search.In this paper,we propose an ABC algorithm based on enhanced local search (ESABC).First,we employ a high-dimension chaotic system Lorenz system)to obtain the ergodic and regular initial populations and to avoid the blindness of random initialization in the population initialization stage.Then,we introduce improved fitness evaluation methods based on the logarithmic function to increase the differences between individuals,reduce selection pressure,and avoid premature convergence.Lastly,inspired by the differential evolution algorithm,we propose a new search tactic that uses the best individual in the contemporary population to guide the renewal of the next generation,and thereby enhance the local search ability.We examined the performance of the proposed approach with 12 classic testing functions and compared the results with the basic and other ABCs.As documented in the experimental results,the proposed algorithm exhibits good optimization performance and can improve both the accuracy and convergence speed of the algorithm. Keywords:artificial bee colony algorithm;high-dimension chaotic system;fitness evaluation;search tactics; optimization algorithm;evolutionary algorithm;convergence analysis;accuracy analysis;intelligent algorithm 人工蜂群算法[1-)是于2005年土耳其学者提 能算法相比,最大的优点在于:开采和开发同时进 出的用于解决优化问题的群智能算法。与其他智 行,增加了寻找到最优解的概率。但它仍然存在收 敛速度慢,易陷入局部最优,开采和开发能力不平 收稿日期:2016-12-23.网络出版日期:2017-05-08. 基金项目:国家自然科学基金资助项目(61203242):物联网云计算平 衡等问题[)。 台建设资助项目(2013H2002):华侨大学研究生科研创新 针对以上问题,许多学者对该算法进行改进研 能力培育计划资助项目(1511322003) 通信作者:柳培忠.E-mail:pzliu@hqu.cdu.cn 究。G.Zhu和S.Kwong受粒子群算法(particle
第 12 卷第 5 期 智 能 系 统 学 报 Vol.12 №.5 2017 年 10 月 CAAI Transactions on Intelligent Systems Oct. 2017 DOI:10.11992 / tis.201612026 网络出版地址:http: / / kns.cnki.net / kcms/ detail / 23.1538.TP.20170508.0922.004.html 一种增强局部搜索能力的改进人工蜂群算法 刘晓芳1 ,柳培忠1 ,骆炎民2 ,范宇凌1 (1. 华侨大学 工学院,福建 泉州 362021; 2. 华侨大学 计算机科学与技术学院,福建 厦门 361021) 摘 要:针对人工蜂群算法初始化群体分布不均匀和局部搜索能力弱的问题,本文提出了一种增强局部搜索能力的 人工蜂群算法(ESABC)。 首先,在种群初始化阶段采用高维洛伦兹混沌系统,得到遍历性好、有规律的初始群体,避 免了随机初始化的盲目性。 然后,采用基于对数函数的适应度评价方式,以增大种群个体间差异,减小选择压力,避 免过早收敛。 最后,在微分进化算法的启发下,提出了一种新的搜索策略,采用当前种群中的最佳个体来引导下一 代的更新,以提高算法的局部搜索能力。 通过对 12 个经典测试函数的仿真实验,并与其他经典的改进人工蜂群算法 对比,结果表明:本文算法具有良好的寻优性能,无论在解的精度还是收敛速度方面效果都有所提高。 关键词:人工蜂群算法;高维混沌系统;适应度评价;搜索策略;优化算法;演化算法;收敛性分析;精度分析;智能 算法 中图分类号:TP18 文献标志码:A 文章编号:1673-4785(2017)05-0684-10 中文引用格式:刘晓芳,柳培忠,骆炎民,等.一种增强局部搜索能力的改进人工蜂群算法[ J]. 智能系统学报, 2017, 12 ( 5): 684-693. 英文引用格式:LIU Xiaofang, LIU Peizhong, LUO Yanmin, et al. Improved artificial bee colony algorithm based on enhanced local search[J]. CAAI transactions on intelligent systems, 2017, 12(5): 684-693. Improved artificial bee colony algorithm based on enhanced local search LIU Xiaofang 1 , LIU Peizhong 1 , LUO Yanmin 2 , FAN Yuling 1 (1. Engineering school, Huaqiao University, Quanzhou 362021, China; 2. School of Computer Science and Technology, Huaqiao University, Xiamen 361021, China) Abstract:The shortcomings of the artificial bee colony algorithm ( ABC ) are its uneven initial population distribution and weak local search. In this paper, we propose an ABC algorithm based on enhanced local search (ESABC). First, we employ a high⁃dimension chaotic system (Lorenz system) to obtain the ergodic and regular initial populations and to avoid the blindness of random initialization in the population initialization stage. Then, we introduce improved fitness evaluation methods based on the logarithmic function to increase the differences between individuals, reduce selection pressure, and avoid premature convergence. Lastly, inspired by the differential evolution algorithm, we propose a new search tactic that uses the best individual in the contemporary population to guide the renewal of the next generation, and thereby enhance the local search ability. We examined the performance of the proposed approach with 12 classic testing functions and compared the results with the basic and other ABCs. As documented in the experimental results, the proposed algorithm exhibits good optimization performance and can improve both the accuracy and convergence speed of the algorithm. Keywords:artificial bee colony algorithm; high⁃dimension chaotic system; fitness evaluation; search tactics; optimization algorithm; evolutionary algorithm; convergence analysis; accuracy analysis; intelligent algorithm 收稿日期:2016-12-23. 网络出版日期:2017-05-08. 基金项目:国家自然科学基金资助项目(61203242); 物联网云计算平 台建设资助项目( 2013H2002); 华侨大学研究生科研创新 能力培育计划资助项目(1511322003). 通信作者:柳培忠. E⁃mail:pzliu@ hqu.edu.cn. 人工蜂群算法[1-3] 是于 2005 年土耳其学者提 出的用于解决优化问题的群智能算法。 与其他智 能算法相比,最大的优点在于:开采和开发同时进 行,增加了寻找到最优解的概率。 但它仍然存在收 敛速度慢,易陷入局部最优,开采和开发能力不平 衡等问题[4] 。 针对以上问题,许多学者对该算法进行改进研 究。 G. Zhu 和 S. Kwong [5]受粒子群算法( particle

第5期 刘晓芳,等:一种增强局部搜索能力的改进人工蜂群算法 .685. swarm optimization,PS0)[6的启发,提出了一种改 解的下界和上界。 进算法(gbest-quide ABC,GABC),通过把全局最优 然后,采蜜蜂在食物源邻域进行搜索,寻找优 解加入到原始的搜索方程中,引导粒子向全局最优 良食物源的位置。当采蜜蜂搜索到食物源时,评估 的方向更新,并通过测试函数验证了其有效性。 该食物源的适应度值。若该食物源具有较好的适 Gao和Liu[7-)对人工蜂群算法的改进进行了众多 应度值,则用新的食物源取代原来的食物源,否则 研究:在2011年,提出了IABC,采用logistic混沌映 不做更新。食物源邻域的搜索方程如式(2)所示: 射进行初始化,并使用了ABC/best/I和ABC/ :=x:+9(x'-x) (2) rand/1两个搜索策略[):2012年,提出MABC,通过 式中:x表示第i个食物源的第j维,g为[-1,1] 正弦迭代器和反向学习方法进行初始化改进,并采 范围内的随机数,ie[1,SN],je[1,D],k为随机选 用ABC/bst/1进行迭代更新,具有很好的收敛性并 择的整数,k∈[1,SN],且k≠i。采用贪婪选择机制 得到了较高质量的解]:2013年,提出PABC,采用 根据适应度值选择V和X:。 Powell方法作为局部搜索工具以提高局部搜索能 对于最小化问题,适应度值的计算公式如式 力[9):2014年,提出EABC,在采蜜蜂阶段和观察蜂 (3)所示: 阶段分别采用两种不同的搜索方程,以达到平衡开 1/(1+f),f≥0 发和开采能力的效果[o:2015年,提出BABC,在观 ft:=1+abs),≤0 (3) 察蜂阶段采用高斯搜索方程生成新的候选个体提 式中:f表示V:对应的函数值,f越小,则t,越大。 高开采能力]。虽然许多学者已对人工蜂群算法 贪婪选择机制的公式如式(4)所示: 进行了各种改进,并取得了良好的效果,但是仍存 在收敛速度慢、局部搜索能力弱的缺点,可继续 P(X,)=)=,)≥fx) (4) (0,f(v)<f(x;) 改进。 式中:T表示蜜蜂个体间的一种映射关系,该式子 针对以上问题,本文提出了一种收敛速度更 能够确保种群中始终保留精英个体,即进化方向不 快、局部搜索能力更强的人工蜂群算法。该算法采 会出现倒退现象。 用高维混沌系统进行初始化,避免随机初始化带来 采蜜蜂搜索结束后,进入观察峰阶段,该类蜜 的盲目性;并采用一种新的搜索策略,通过当前种 蜂指待在蜂巢内等待采蜜蜂采到食物源后返回分 群中的最优解引导进化方向,增强算法的局部搜索 享食物源信息的个体。因此,观察蜂需要根据概率 能力,进而达到提高解精度的效果,并且通过基于 来选择将要跟随的采蜜蜂。概率选择公式如式(5) 对数函数的适应度评价方式,增大个体间差异,减 所示: 小选择压力,更容易选择出优秀个体。 fit, P:= (5) 基本的人工蜂群算法 在人工蜂群算法中,把蜜蜂种群分为3种类型, 当观察蜂根据式(5)选择到采蜜蜂进行跟随时,接 即采蜜蜂、观察蜂和侦察蜂,把蜜蜂的行为分为以 下来观察蜂根据采蜜蜂共享的信息,到其附近进行 下3种,即搜索、招募和放弃)。在蜜蜂种群中取 局部深度搜索,搜索公式同式(2),然后再通过适应 一半作为采蜜蜂,另一半作为观察蜂。蜜蜂种群在 度值评估食物源的质量。 多维搜索空间中更新时,采蜜蜂负责根据自身经验 在经过一定次数的迭代之后(用imit表示迭代 搜索食物源,然后把食物源的具体信息告诉观察 次数),若采蜜蜂或者观察蜂的食物源的质量一直 蜂;观察蜂根据采蜜蜂共享的信息选择将要跟随的 没有更新,则认为该蜜蜂个体陷入了局部最优,此 蜜蜂:侦察蜂在食物源经过有限次搜索后仍未更新 时放弃该食物源,并且采蜜蜂或观察蜂转变为侦察 时发挥作用,重新初始化种群生成新的食物源。在 蜂,然后侦察蜂将会根据式(2)生成新的蜜蜂群体 优化问题中,食物源与优化问题的可行解相对应, (新的可行解),进而跳出局部最优。 采集食物源的过程相当于搜索最优解的过程。解 的好坏取决于优化问题的适应度值,即较高的适应 2 改进的人工蜂群算法 度值代表较好的食物源(可行解)。 在原始的人工蜂群算法中,初始种群由随机函 首先,该算法根据公式(1)随机生成初始食物 数产生,所以该算法具有较强的全局搜索能力。但 源(初始解): 是,原始搜索方程的局部搜索能力比较弱,导致对 =x+rand(0,1)( (1) 解没有充分开采。全局搜索能力和局部搜索能力 式中:i=1,2,…,SN;j=1,2,…,D:SN代表食物源 的不平衡是影响收敛速度和解质量的关键因素之 (解)的个数;D表示解的维数;xi和xi分别表示 一。另外,搜索进行到后期时,种群多样性会有所
swarm optimization, PSO) [6] 的启发,提出了一种改 进算法(gbest⁃guide ABC, GABC),通过把全局最优 解加入到原始的搜索方程中,引导粒子向全局最优 的方向更新, 并通过测试函数验证了其有效性。 Gao 和 Liu [7-11]对人工蜂群算法的改进进行了众多 研究:在 2011 年,提出了 IABC,采用 logistic 混沌映 射进 行 初 始 化, 并 使 用 了 ABC / best / 1 和 ABC / rand / 1两个搜索策略[7] ;2012 年,提出 MABC,通过 正弦迭代器和反向学习方法进行初始化改进,并采 用 ABC / best / 1 进行迭代更新,具有很好的收敛性并 得到了较高质量的解[8] ;2013 年,提出 PABC,采用 Powell 方法作为局部搜索工具以提高局部搜索能 力[9] ;2014 年,提出 EABC,在采蜜蜂阶段和观察蜂 阶段分别采用两种不同的搜索方程,以达到平衡开 发和开采能力的效果[10] ;2015 年,提出 BABC,在观 察蜂阶段采用高斯搜索方程生成新的候选个体提 高开采能力[11] 。 虽然许多学者已对人工蜂群算法 进行了各种改进,并取得了良好的效果,但是仍存 在收敛速度慢、 局部搜索能力弱的缺点, 可继续 改进。 针对以上问题,本文提出了一种收敛速度更 快、局部搜索能力更强的人工蜂群算法。 该算法采 用高维混沌系统进行初始化,避免随机初始化带来 的盲目性;并采用一种新的搜索策略,通过当前种 群中的最优解引导进化方向,增强算法的局部搜索 能力,进而达到提高解精度的效果,并且通过基于 对数函数的适应度评价方式,增大个体间差异,减 小选择压力,更容易选择出优秀个体。 1 基本的人工蜂群算法 在人工蜂群算法中,把蜜蜂种群分为 3 种类型, 即采蜜蜂、观察蜂和侦察蜂,把蜜蜂的行为分为以 下 3 种,即搜索、招募和放弃[2] 。 在蜜蜂种群中取 一半作为采蜜蜂,另一半作为观察蜂。 蜜蜂种群在 多维搜索空间中更新时,采蜜蜂负责根据自身经验 搜索食物源,然后把食物源的具体信息告诉观察 蜂;观察蜂根据采蜜蜂共享的信息选择将要跟随的 蜜蜂;侦察蜂在食物源经过有限次搜索后仍未更新 时发挥作用,重新初始化种群生成新的食物源。 在 优化问题中,食物源与优化问题的可行解相对应, 采集食物源的过程相当于搜索最优解的过程。 解 的好坏取决于优化问题的适应度值,即较高的适应 度值代表较好的食物源(可行解)。 首先,该算法根据公式(1) 随机生成初始食物 源(初始解): x j i = x j min + rand(0,1)(x j max - x j min ) (1) 式中:i = 1,2,…,SN;j = 1,2,…,D;SN 代表食物源 (解)的个数;D 表示解的维数;x j min和 x j max分别表示 解的下界和上界。 然后,采蜜蜂在食物源邻域进行搜索,寻找优 良食物源的位置。 当采蜜蜂搜索到食物源时,评估 该食物源的适应度值。 若该食物源具有较好的适 应度值,则用新的食物源取代原来的食物源,否则 不做更新。 食物源邻域的搜索方程如式(2)所示: v j i = x j i + φ j i (x j i - x j k ) (2) 式中:x j i 表示第 i 个食物源的第 j 维,φ j i 为[ -1,1] 范围内的随机数,i∈[1,SN],j∈[1,D],k 为随机选 择的整数,k∈[1,SN],且 k≠i。 采用贪婪选择机制 根据适应度值选择 Vi 和 Xi。 对于最小化问题,适应度值的计算公式如式 (3)所示: fit i = 1 / (1 + f i), f i ≥ 0 1 + abs(f i), f i ≤ 0 { (3) 式中: f i 表示 Vi 对应的函数值,f i 越小,则fit i 越大。 贪婪选择机制的公式如式(4)所示: P Ts(Xi,Vi) = Vi { } = 1, f(Vi) ≥ f(Xi) 0, f(Vi) < f(Xi) { (4) 式中:Ts 表示蜜蜂个体间的一种映射关系,该式子 能够确保种群中始终保留精英个体,即进化方向不 会出现倒退现象。 采蜜蜂搜索结束后,进入观察峰阶段,该类蜜 蜂指待在蜂巢内等待采蜜蜂采到食物源后返回分 享食物源信息的个体。 因此,观察蜂需要根据概率 来选择将要跟随的采蜜蜂。 概率选择公式如式(5) 所示: pi = fit i ∑ SN i = 1 fit i (5) 当观察蜂根据式(5)选择到采蜜蜂进行跟随时,接 下来观察蜂根据采蜜蜂共享的信息,到其附近进行 局部深度搜索,搜索公式同式(2),然后再通过适应 度值评估食物源的质量。 在经过一定次数的迭代之后(用 limit 表示迭代 次数),若采蜜蜂或者观察蜂的食物源的质量一直 没有更新,则认为该蜜蜂个体陷入了局部最优,此 时放弃该食物源,并且采蜜蜂或观察蜂转变为侦察 蜂,然后侦察蜂将会根据式(2)生成新的蜜蜂群体 (新的可行解),进而跳出局部最优。 2 改进的人工蜂群算法 在原始的人工蜂群算法中,初始种群由随机函 数产生,所以该算法具有较强的全局搜索能力。 但 是,原始搜索方程的局部搜索能力比较弱,导致对 解没有充分开采。 全局搜索能力和局部搜索能力 的不平衡是影响收敛速度和解质量的关键因素之 一。 另外,搜索进行到后期时,种群多样性会有所 第 5 期 刘晓芳,等:一种增强局部搜索能力的改进人工蜂群算法 ·685·

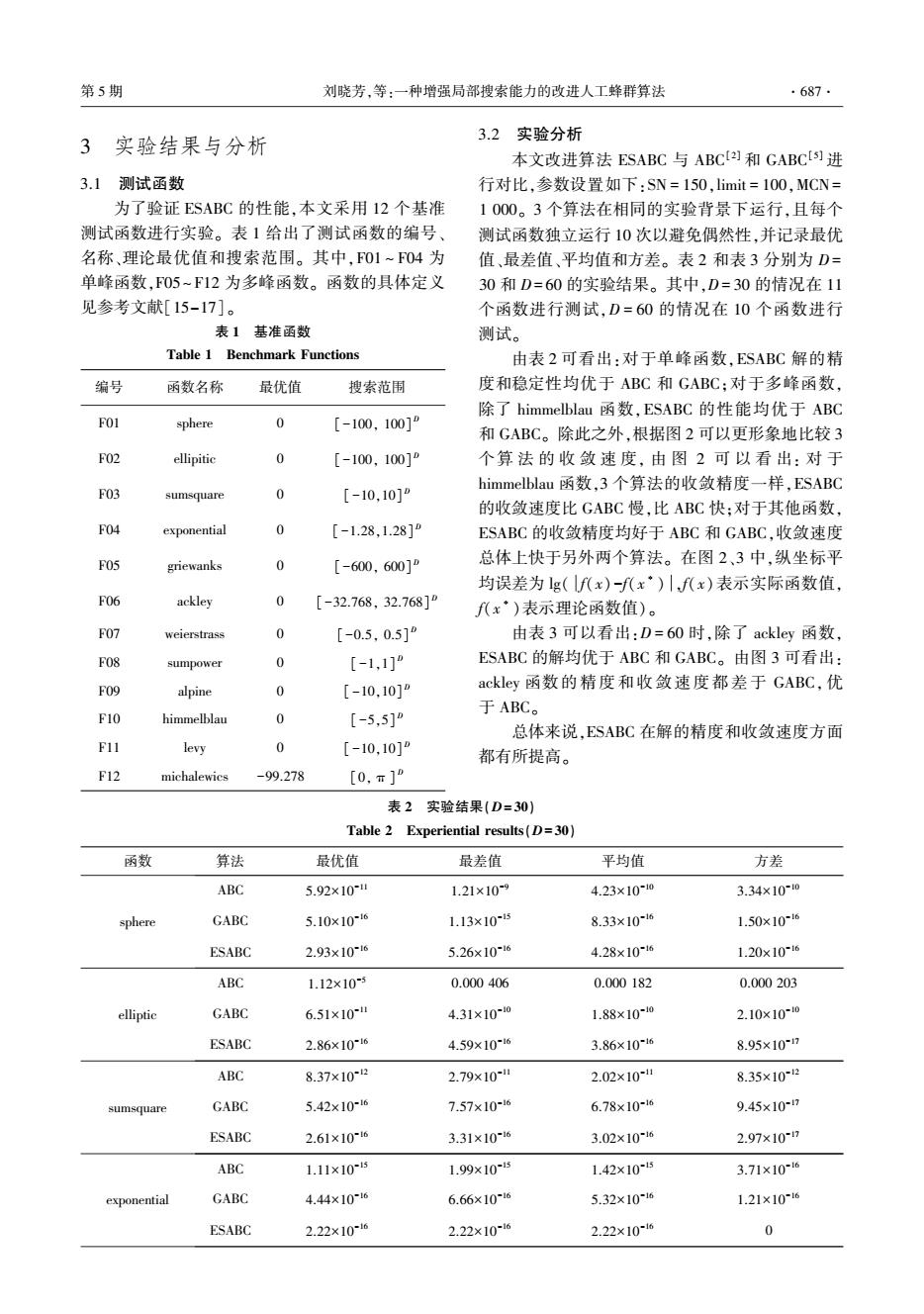
·686 智能系统学报 第12卷 下降,严重影响算法的搜索效率。针对以上问题, 2.3新的搜索机制 本文提出3个改进策略提高算法的性能。 因为搜索能力不平衡会导致寻优能力下降,所 2.1种群初始化 以平衡算法的开发(全局搜索)和开采(局部搜索) 种群初始解的质量在一定程度上影响最终解 能力是提高算法性能的措施之一。从原始人工蜂 的质量,初始解分布越均匀,覆盖越广泛,在最优解 群算法的搜索方程式(2)可以看出:系数9是[-1, 邻域搜索的可能性就越大。所以,我们需要设计一 1]中的一个随机数,参数j和k为[1,D]中的随机 种策略增加种群多样性。 整数,这些随机数使得算法具有较好的全局搜索能 混沌是一种非线性现象,具有随机性、遍历性 力,而局部搜索能力较弱。所以,需要设计一种局 和有界性。在一定范围内,根据规则可不重复地转 部搜索能力较强的搜索策略平衡搜索能力。受微 变成所有状态。B.Alatas2]已证明混沌映射是一 分进化算法[1)的启发,本文提出了一种新的搜索策 种可有效地在整个搜索空间搜索解的方法。目前, 略,如式(9)所示: 应用在群智能算法上的混沌系统大多数为一维的, =x+中,(x-x,) (9) 但是,一维混沌系统具有以下不足:1)迭代操作后 式中:r为{1,2,…,SN}内的随机整数,且r≠i;i和j 产生单一序列:2)分布不均匀。因此,本文提出采 的含义同式(2):中:为[-1,1]内的随机数:x,为第 用一种高维的混沌系统—洛伦兹混沌系统,该系 个蜜蜂的第j维;x代表当代种群中最优个体的第方 统可产生3个不同的混沌迭代序列,增加了优良序 维,即当前种群最优解引导下一代个体的进化方向, 列的可选择性,提高了序列的分布性。混沌迭代序 可以达到增强局部搜索能力和提高解精度的效果。 列的生成公式如式(6)所示: 2.4改进算法流程图 宝=6(y-x) 通过以上分析可得出:以上策略可以平衡算法 y=yx-y-xz (6) 的搜索能力,提高算法的性能。改进算法的具体流 i=xy-Bz 程如图1所示。 式中:取x(0)y(0)、z(0)为初始值;6、yB为洛伦 开始 兹系统的参数,取值分别为6=10,B=8/3,y>24.74。 由高维混沌系统初始化种群个体,参数初始化: 最后,从产生的三组混沌序列中随机选一维,记作 种群大小(SN),最大迭代次数(MCN),维数(D) P,把该参数代入式(1),得到新的初始化方程,如式 (7)所示: 根据公式(8)计算函数 的适应度值,记作 x=xdm+p(xi-xm) (7) 式中:i=1,2,…,SN;j=1,2,…,D:SN表示食物源 随机选取初始群体的一半作为 (解)的数量:D表示解的维数:P由混沌系统得到: 采蜜蜂,另一半作为观察蜂 x和x分别为函数的下界和上界。由混沌系统 采蜜蜂根据公式(9) 得出的p与随机参数rand(0,1)相比,可避免初始 局部搜索新食物湖 解的盲目性。 计算适应度值,记作fit new,若it<fit new, 更新当前采蜜蜂,trial(i=0,否则,trial(i)+ 2.2改进的适应度评价方式 在原始人工蜂群算法中,观察蜂通过式(5)的 观察蜂根据公式(5)计算选择概率P,以概率P()搜索新食物 概率选择优良食物源跟随,进行局部开采。概率的 源,然后转化为采蜜蜂进行邻域搜索,根据公式(8)计算其 大小反映了采蜜蜂携带食物源的质量,食物源质量 适应度值,比较并判断是否更新,修改标志向量trial() 通过适应度值体现,适应度值越大,食物源质量越 好,被选择的概率就越大。但是,在式(3)中,当函 Trial()>limit Y 数值方满足条件limf=0,limf=0,f≠f时,适应度 第个采蜜蜂转换为侦察蜂 值则lim fit,=1,lim fit,=1,那么公式(5)中的概率值 随机产生新食物源 也会相同,体现不出个体之间的差异)。为了解决 该问题,本文采用基于对数的适应度评价方式,通 记录当前全局最优 过该方法把个体间差异明显化,进而把函数值相似 但不同的种群个体区分开,使得优秀个体有更大的 <iter>MCN 概率被跟随开采[)]。改进后的适应度评价方式如 Y 式(8)所示: 结束☐ fit,=0/(0.1+1/lgfl),0≤f≤10-(8) 图1 ESABC算法流程图 式中:入由计算机的计算精度决定。此处,取入=8。 Fig.1 ESABC flowchat
下降,严重影响算法的搜索效率。 针对以上问题, 本文提出 3 个改进策略提高算法的性能。 2.1 种群初始化 种群初始解的质量在一定程度上影响最终解 的质量,初始解分布越均匀,覆盖越广泛,在最优解 邻域搜索的可能性就越大。 所以,我们需要设计一 种策略增加种群多样性。 混沌是一种非线性现象,具有随机性、遍历性 和有界性。 在一定范围内,根据规则可不重复地转 变成所有状态。 B. Alatas [12] 已证明混沌映射是一 种可有效地在整个搜索空间搜索解的方法。 目前, 应用在群智能算法上的混沌系统大多数为一维的, 但是,一维混沌系统具有以下不足:1) 迭代操作后 产生单一序列;2) 分布不均匀。 因此,本文提出采 用一种高维的混沌系统———洛伦兹混沌系统,该系 统可产生 3 个不同的混沌迭代序列,增加了优良序 列的可选择性,提高了序列的分布性。 混沌迭代序 列的生成公式如式(6)所示: x · = δ(y - x) y · = γx - y - xz z · = xy - βz ì î í ï ï ïï (6) 式中:取 x(0)、y(0)、z(0)为初始值;δ、γ、β 为洛伦 兹系统的参数,取值分别为 δ = 10,β = 8 / 3,γ>24.74。 最后,从产生的三组混沌序列中随机选一维,记作 φ,把该参数代入式(1),得到新的初始化方程,如式 (7)所示: x j i = x j min + φ(x j max - x j min ) (7) 式中:i = 1,2,…,SN;j = 1,2,…,D;SN 表示食物源 (解)的数量;D 表示解的维数;φ 由混沌系统得到; x j min和 x j max分别为函数的下界和上界。 由混沌系统 得出的 φ 与随机参数 rand(0,1)相比,可避免初始 解的盲目性。 2.2 改进的适应度评价方式 在原始人工蜂群算法中,观察蜂通过式(5) 的 概率选择优良食物源跟随,进行局部开采。 概率的 大小反映了采蜜蜂携带食物源的质量,食物源质量 通过适应度值体现,适应度值越大,食物源质量越 好,被选择的概率就越大。 但是,在式(3) 中,当函 数值 f i 满足条件 lim f i = 0,lim f j = 0,f i≠f j 时,适应度 值则 lim fit i = 1,lim fit j = 1,那么公式(5)中的概率值 也会相同,体现不出个体之间的差异[8] 。 为了解决 该问题,本文采用基于对数的适应度评价方式,通 过该方法把个体间差异明显化,进而把函数值相似 但不同的种群个体区分开,使得优秀个体有更大的 概率被跟随开采[13] 。 改进后的适应度评价方式如 式(8)所示: fit i = 0.1/ (0.1 + 1/ lg f i ), 0 ≤ f i ≤10 -λ (8) 式中:λ 由计算机的计算精度决定。 此处,取 λ = 8。 2.3 新的搜索机制 因为搜索能力不平衡会导致寻优能力下降,所 以平衡算法的开发(全局搜索)和开采(局部搜索) 能力是提高算法性能的措施之一。 从原始人工蜂 群算法的搜索方程式(2)可以看出:系数 φ j i 是[ -1, 1]中的一个随机数,参数 j 和 k 为 [1,D]中的随机 整数,这些随机数使得算法具有较好的全局搜索能 力,而局部搜索能力较弱。 所以,需要设计一种局 部搜索能力较强的搜索策略平衡搜索能力。 受微 分进化算法[14]的启发,本文提出了一种新的搜索策 略,如式(9)所示: v j i = x j best + ϕ j i (x j best - x j r ) (9) 式中:r 为{1,2,…,SN} 内的随机整数,且 r≠i;i 和 j 的含义同式(2);ϕ j i 为[-1,1]内的随机数;x j r 为第 r 个蜜蜂的第 j 维;x j best代表当代种群中最优个体的第 j 维,即当前种群最优解引导下一代个体的进化方向, 可以达到增强局部搜索能力和提高解精度的效果。 2.4 改进算法流程图 通过以上分析可得出:以上策略可以平衡算法 的搜索能力,提高算法的性能。 改进算法的具体流 程如图 1 所示。 图 1 ESABC 算法流程图 Fig.1 ESABC flowchat ·686· 智 能 系 统 学 报 第 12 卷
第5期 刘晓芳,等:一种增强局部搜索能力的改进人工蜂群算法 .687. 3 实验结果与分析 3.2实验分析 本文改进算法ESABC与ABC2]和GABC)进 3.1 测试函数 行对比,参数设置如下:SN=150,limit=100,MCN= 为了验证ESABC的性能,本文采用12个基准 1000.3个算法在相同的实验背景下运行,且每个 测试函数进行实验。表1给出了测试函数的编号、 测试函数独立运行10次以避免偶然性,并记录最优 名称、理论最优值和搜索范围。其中,01~F04为 值、最差值、平均值和方差。表2和表3分别为D= 单峰函数,F05~F12为多峰函数。函数的具体定义 30和D=60的实验结果。其中,D=30的情况在11 见参考文献[15-17]。 个函数进行测试,D=60的情况在10个函数进行 表1基准函数 测试。 Table 1 Benchmark Functions 由表2可看出:对于单峰函数,ESABC解的精 编号 函数名称 最优值 搜索范围 度和稳定性均优于ABC和GABC:对于多峰函数, 除了himmelblau函数,ESABC的性能均优于ABC FO1 sphere [-100,100]P 和GABC。除此之外,根据图2可以更形象地比较3 F02 ellipitic 0 [-100,100]0 个算法的收敛速度,由图2可以看出:对于 himmelblau函数,3个算法的收敛精度一样,ESABC F03 sumsquare [-10,10]° 的收敛速度比GABC慢,比ABC快:对于其他函数, F04 exponential 0 [-1.28,1.28]0 ESABC的收敛精度均好于ABC和GABC,收敛速度 F05 griewanks [-600,600]° 总体上快于另外两个算法。在图2、3中,纵坐标平 均误差为g(f(x)-f(x·)|f代x)表示实际函数值, F06 ackley 0 [-32.768,32.768] f(x)表示理论函数值)。 F07 weierstrass 0 [-0.5,0.5]° 由表3可以看出:D=60时,除了ackley函数, F08 sumpower [-1,1]P ESABC的解均优于ABC和GABC。由图3可看出: F09 alpine 0 [-10,10] ackley函数的精度和收敛速度都差于GABC,优 F10 himmelblau 0 [-5,5]P 于ABC。 总体来说,ESABC在解的精度和收敛速度方面 F11 levy 0 [-10,10]° 都有所提高。 F12 michalewics -99.278 [0,r] 表2实验结果(D=30) Table 2 Experiential results(D=30) 函数 算法 最优值 最差值 平均值 方差 ABC 5.92×10~1 1.21×10 4.23×10-0 3.34×10-0 sphere GABC 5.10×10~16 1.13×105 8.33×10-16 1.50×10i6 ESABC 2.93×1016 5.26×10-6 4.28×10-16 1.20×106 ABC 1.12×10 0.000406 0.000182 0.000203 elliptic GABC 6.51×10n 4.31×10-0 1.88×10-10 2.10x100 ESABC 2.86×1016 4.59×10-6 3.86×10-16 8.95×10n ABC 8.37x102 2.79x101 2.02×1011 8.35×10-12 sumsquare GABC 5.42×1016 7.57×1016 6.78×10-16 9.45×10n ESABC 2.61×1016 3.31×1016 3.02×1016 2.97x107 ABC 1.11×105 1.99x105 1.42×10~5 3.71×10~16 exponential GABC 4.44×106 6.66×10-6 5.32×10~6 1.21×106 ESABO 2.22×10-16 2.22×10-16 2.22×10-16 0
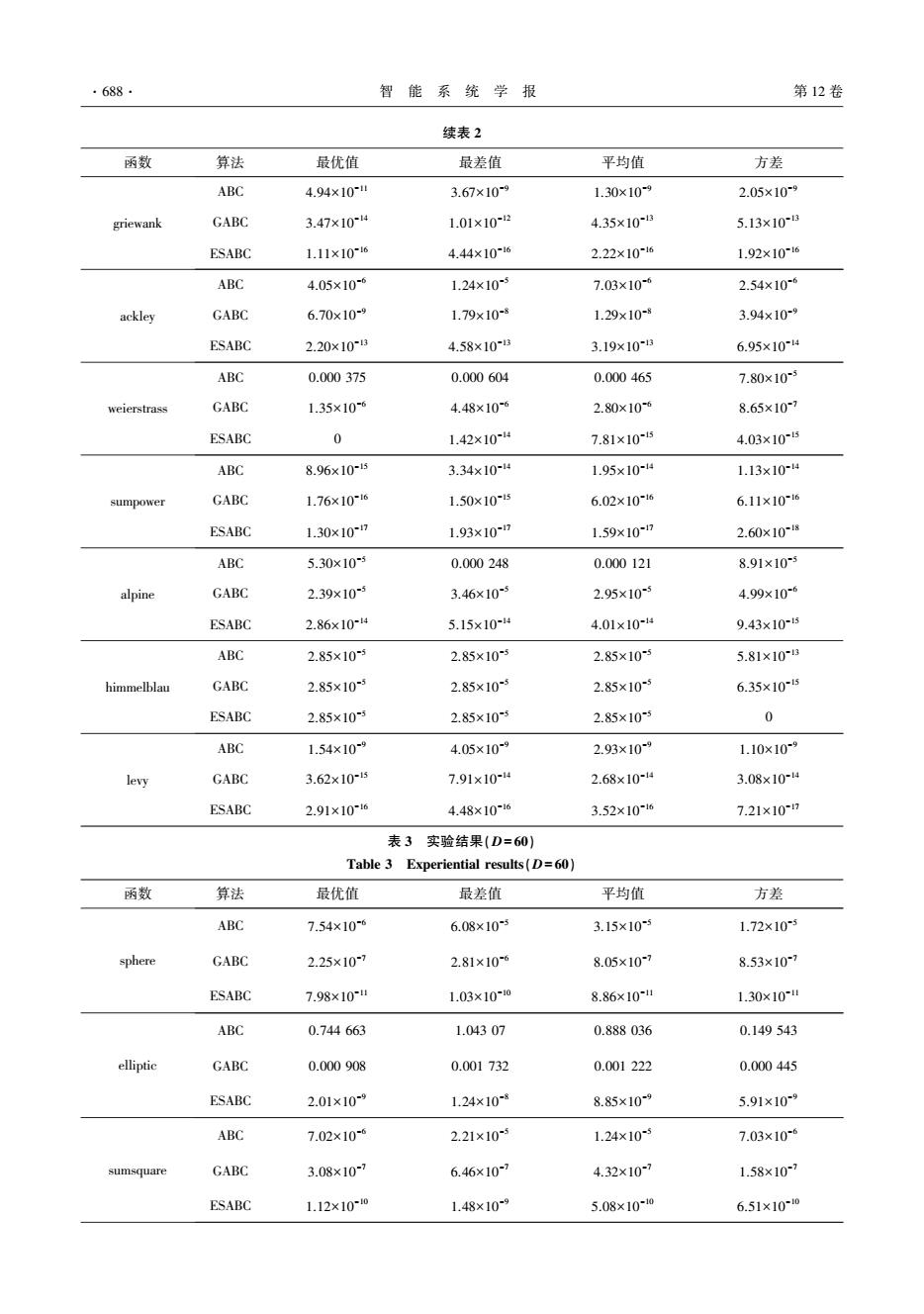
3 实验结果与分析 3.1 测试函数 为了验证 ESABC 的性能,本文采用 12 个基准 测试函数进行实验。 表 1 给出了测试函数的编号、 名称、理论最优值和搜索范围。 其中,F01 ~ F04 为 单峰函数,F05~ F12 为多峰函数。 函数的具体定义 见参考文献[15-17]。 表 1 基准函数 Table 1 Benchmark Functions 编号 函数名称 最优值 搜索范围 F01 sphere 0 [-100, 100] D F02 ellipitic 0 [-100, 100] D F03 sumsquare 0 [-10,10] D F04 exponential 0 [-1.28,1.28] D F05 griewanks 0 [-600, 600] D F06 ackley 0 [-32.768, 32.768] D F07 weierstrass 0 [-0.5, 0.5] D F08 sumpower 0 [-1,1] D F09 alpine 0 [-10,10] D F10 himmelblau 0 [-5,5] D F11 levy 0 [-10,10] D F12 michalewics -99.278 [0, π ] D 3.2 实验分析 本文改进算法 ESABC 与 ABC [2] 和 GABC [5] 进 行对比,参数设置如下:SN = 150,limit = 100,MCN= 1 000。 3 个算法在相同的实验背景下运行,且每个 测试函数独立运行 10 次以避免偶然性,并记录最优 值、最差值、平均值和方差。 表 2 和表 3 分别为 D = 30 和 D= 60 的实验结果。 其中,D= 30 的情况在 11 个函数进行测试,D = 60 的情况在 10 个函数进行 测试。 由表 2 可看出:对于单峰函数,ESABC 解的精 度和稳定性均优于 ABC 和 GABC;对于多峰函数, 除了 himmelblau 函数,ESABC 的性能均优于 ABC 和 GABC。 除此之外,根据图 2 可以更形象地比较 3 个算 法 的 收 敛 速 度, 由 图 2 可 以 看 出: 对 于 himmelblau 函数,3 个算法的收敛精度一样,ESABC 的收敛速度比 GABC 慢,比 ABC 快;对于其他函数, ESABC 的收敛精度均好于 ABC 和 GABC,收敛速度 总体上快于另外两个算法。 在图 2、3 中,纵坐标平 均误差为 lg( f(x)-f(x ∗ ) ,f(x)表示实际函数值, f(x ∗ )表示理论函数值)。 由表 3 可以看出:D = 60 时,除了 ackley 函数, ESABC 的解均优于 ABC 和 GABC。 由图 3 可看出: ackley 函数的精度和收敛速度都差于 GABC, 优 于 ABC。 总体来说,ESABC 在解的精度和收敛速度方面 都有所提高。 表 2 实验结果(D= 30) Table 2 Experiential results(D= 30) 函数 算法 最优值 最差值 平均值 方差 sphere ABC 5.92×10 -11 1.21×10 -9 4.23×10 -10 3.34×10 -10 GABC 5.10×10 -16 1.13×10 -15 8.33×10 -16 1.50×10 -16 ESABC 2.93×10 -16 5.26×10 -16 4.28×10 -16 1.20×10 -16 elliptic ABC 1.12×10 -5 0.000 406 0.000 182 0.000 203 GABC 6.51×10 -11 4.31×10 -10 1.88×10 -10 2.10×10 -10 ESABC 2.86×10 -16 4.59×10 -16 3.86×10 -16 8.95×10 -17 sumsquare ABC 8.37×10 -12 2.79×10 -11 2.02×10 -11 8.35×10 -12 GABC 5.42×10 -16 7.57×10 -16 6.78×10 -16 9.45×10 -17 ESABC 2.61×10 -16 3.31×10 -16 3.02×10 -16 2.97×10 -17 exponential ABC 1.11×10 -15 1.99×10 -15 1.42×10 -15 3.71×10 -16 GABC 4.44×10 -16 6.66×10 -16 5.32×10 -16 1.21×10 -16 ESABC 2.22×10 -16 2.22×10 -16 2.22×10 -16 0 第 5 期 刘晓芳,等:一种增强局部搜索能力的改进人工蜂群算法 ·687·
·688. 智能系统学报 第12卷 续表2 函数 算法 最优值 最差值 平均值 方差 ABC 4.94×10" 3.67×109 1.30×109 2.05×10 griewank GABC 3.47×1014 1.01×102 4.35×10B 5.13×10-3 ESABC 1.11×1016 4.44×1016 2.22×106 1.92×1016 ABC 4.05×10-6 1.24×10 7.03×10-6 2.54×10-6 ackley GABC 6.70x10-9 1.79×10-s 1.29×10-8 3.94×109 ESABC 2.20×103 4.58×10-18 3.19×108 6.95×10-14 ABC 0.000375 0.000604 0.000465 7.80×105 weierstrass GABC 1.35×10-6 4.48×10-6 2.80×10-6 8.65×107 ESABC 0 1.42×1014 7.81×10-15 4.03x10-5 ABC 8.96×10-15 3.34×10-4 1.95×10-14 1.13×10-4 sumpower GABC 1.76×10-16 1.50x10-5 6.02×10-16 6.11×1016 ESABC 1.30x10 1.93x10n 1.59x10 2.60×1018 ABC 5.30×10- 0.000248 0.000121 8.91×105 alpine GABC 2.39×10- 3.46×105 2.95×105 4.99×106 ESABC 2.86×104 5.15×104 4.01×1014 9.43×105 ABC 2.85×105 2.85×105 2.85×105 5.81×103 himmelblau GABC 2.85×10- 2.85×10 2.85×105 6.35×10-5 ESABC 2.85×10 2.85×10 2.85×105 0 ABC 1.54×109 4.05×109 2.93×109 1.10×10-9 levy GABC 3.62x10-15 7.91×10-14 2.68×10-14 3.08×104 ESABC 2.91×10-16 4.48×10-6 3.52×10-16 7.21×107 表3实验结果(D=60) Table 3 Experiential results(D=60) 函数 算法 最优值 最差值 平均值 方差 ABC 7.54×10-6 6.08×10 3.15×10-5 1.72×10-5 sphere GABC 2.25×10-7 2.81×10-6 8.05×10-7 8.53×107 ESABC 7.98×101 1.03×10-0 8.86×1011 1.30×104 ABC 0.744663 1.04307 0.888036 0.149543 elliptic GABC 0.000908 0.001732 0.001222 0.000445 ESABC 2.01×10-9 1.24×10- 8.85×10-9 5.91×109 ABC 7.02×10-6 2.21×10-5 1.24×105 7.03×106 sumsquare GABC 3.08×107 6.46×107 4.32×10-7 1.58×10-7 ESABC 1.12×100 1.48×10-9 5.08×10-0 6.51×1010
续表 2 函数 算法 最优值 最差值 平均值 方差 griewank ABC 4.94×10 -11 3.67×10 -9 1.30×10 -9 2.05×10 -9 GABC 3.47×10 -14 1.01×10 -12 4.35×10 -13 5.13×10 -13 ESABC 1.11×10 -16 4.44×10 -16 2.22×10 -16 1.92×10 -16 ackley ABC 4.05×10 -6 1.24×10 -5 7.03×10 -6 2.54×10 -6 GABC 6.70×10 -9 1.79×10 -8 1.29×10 -8 3.94×10 -9 ESABC 2.20×10 -13 4.58×10 -13 3.19×10 -13 6.95×10 -14 weierstrass ABC 0.000 375 0.000 604 0.000 465 7.80×10 -5 GABC 1.35×10 -6 4.48×10 -6 2.80×10 -6 8.65×10 -7 ESABC 0 1.42×10 -14 7.81×10 -15 4.03×10 -15 sumpower ABC 8.96×10 -15 3.34×10 -14 1.95×10 -14 1.13×10 -14 GABC 1.76×10 -16 1.50×10 -15 6.02×10 -16 6.11×10 -16 ESABC 1.30×10 -17 1.93×10 -17 1.59×10 -17 2.60×10 -18 alpine ABC 5.30×10 -5 0.000 248 0.000 121 8.91×10 -5 GABC 2.39×10 -5 3.46×10 -5 2.95×10 -5 4.99×10 -6 ESABC 2.86×10 -14 5.15×10 -14 4.01×10 -14 9.43×10 -15 himmelblau ABC 2.85×10 -5 2.85×10 -5 2.85×10 -5 5.81×10 -13 GABC 2.85×10 -5 2.85×10 -5 2.85×10 -5 6.35×10 -15 ESABC 2.85×10 -5 2.85×10 -5 2.85×10 -5 0 levy ABC 1.54×10 -9 4.05×10 -9 2.93×10 -9 1.10×10 -9 GABC 3.62×10 -15 7.91×10 -14 2.68×10 -14 3.08×10 -14 ESABC 2.91×10 -16 4.48×10 -16 3.52×10 -16 7.21×10 -17 表 3 实验结果(D= 60) Table 3 Experiential results(D= 60) 函数 算法 最优值 最差值 平均值 方差 sphere ABC 7.54×10 -6 6.08×10 -5 3.15×10 -5 1.72×10 -5 GABC 2.25×10 -7 2.81×10 -6 8.05×10 -7 8.53×10 -7 ESABC 7.98×10 -11 1.03×10 -10 8.86×10 -11 1.30×10 -11 elliptic ABC 0.744 663 1.043 07 0.888 036 0.149 543 GABC 0.000 908 0.001 732 0.001 222 0.000 445 ESABC 2.01×10 -9 1.24×10 -8 8.85×10 -9 5.91×10 -9 sumsquare ABC 7.02×10 -6 2.21×10 -5 1.24×10 -5 7.03×10 -6 GABC 3.08×10 -7 6.46×10 -7 4.32×10 -7 1.58×10 -7 ESABC 1.12×10 -10 1.48×10 -9 5.08×10 -10 6.51×10 -10 ·688· 智 能 系 统 学 报 第 12 卷