【智能系统】基于系统动力学模型的物元相关网研究

第12卷第4期 智能系统学报 Vol.12 No.4 2017年8月 CAAI Transactions on Intelligent Systems Aug.2017 D0I:10.11992/is.201610013 网络出版地址：http://kns.cmki.net/kcms/detail/23.1538.tp.20170407.1758.020.html 基于系统动力学模型的物元相关网研究 李文军12，杨春燕12 (1.广东工业大学可拓学与创新方法研究所，广东广州510006：2.广东工业大学机电工程学院，广东广州510006) 摘要：在可拓学相关分析理论中，关键在于确定相关基元的函数关系。然而，在具体领域中运用的时候，相关函数 的确定往往是比较困难的，也就局限了相关网方法的使用。文章以物元为研究对象，对物元的相关网进行了研究， 提出了相关网的动力学模型建模方法以及一种在相关函数未知的情况下，基于系统动力学模型的物元相关函数近 似构造方法。该方法的原理是通过基础数据的收集和分析，在依据相关网建立的动力学模型中按照固定的步骤进 行模拟分析，得出物元的近似相关函数。在此基础上，相关分析的进行就变得简单、可模拟。案例分析的结果表明， 该方法能够有效模拟和近似构造相关物元之间的函数关系，为相关网方法在具体领域中的运用莫定了一定的基础。 关键词：可拓学；物元；相关分析；相关网；系统动力学；仿真；相关函数；建模 中图分类号：TP18文献标志码：A文章编号：1673-4785(2017)04-0459-09 中文引用格式：李文军，杨春燕.基于系统动力学模型的物元相关网研究[J].智能系统学报，2017,12(4)：459-467. 英文引用格式：LI Wenjun,YANG Chunyan.Research on a correlative network of matter-elements based on a system dynamics model[J].CAAI transactions on intelligent systems,2017,12(4):459-467. Research on a correlative network of matter-elements based on a system dynamics model LI Wenjun'.2,YANG Chunyan'2 (1.Research Institute of Extenics and Innovation Methods,Guangdong University of Technology,Guangzhou 510006,China; 2.School of Electromechanical Engineering,Guangdong University of Technology,Guangzhou 510006,China) Abstract:In the correlative analysis of Extenics,the key is to define the correlation function relating to the basic- elements.However,it is very difficult to define the correlation function when it is applied to specific areas and this limits the usage of the correlative network.In this paper,a correlation network based on matter-elements is studied. Then,we present a method for establishing a system dynamics model of the correlation network and a method for approximately identifying the correlation function based on the system dynamics model,in which the correlation functions under some related matter-elements are unknown.The principle of this method is to derive the approximate correlation functions of related matter-elements according to the principle of collecting and analyzing basic data,and establishing a kinetic model for simulation and analysis in terms of a fixed procedure in the correlative network.In this way,correlative analysis becomes easy and can be simulated.The clear conclusion is that the method efficiently simulates the correlation function and lays the foundation for the application of correlation analysis to specific areas. Keywords:Extenics;matter-element;correlative analysis;correlative network;system dynamics;simulation; correlation functions;modeling 相关网方法是可拓学中建立的利用基元模型 文献[2]研究了复杂系统下相关分析中不同相关特 研究基元之间的相关关系的方法。目前对于复 征量值之间的函数关系，为复杂系统中相关网的进 杂系统下相关网的量化研究较少，而对于复杂系统 一步研究打下了坚实的基础。文献[3-7]基于基元 的研究而言，相关分析是一个很有用的分析方法。 的相关性介绍了传导变换的概念以及传导效应的 计算方法。然而，对于复杂系统的相关网，如果能 收稿日期：2016-10-13.网络出版日期：2017-04-07 用更简单系统化的方法进行分析和研究，为相关函 基金项目：国家自然科学基金项目(61273306)：广东省科技计划项目 (2016A040404015). 数的近似构造提供依据，将会为可拓创意的生成和 通信作者：杨春燕.E-mail:276519106@qg.com

第 １２ 卷第 ４ 期 智 能 系 统 学 报 Ｖｏｌ．１２ №．４ ２０１７ 年 ８ 月 ＣＡＡＩ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｉｎｔｅｌｌｉｇｅｎｔ Ｓｙｓｔｅｍｓ Ａｕｇ． ２０１７ ＤＯＩ：１０．１１９９２ ／ ｔｉｓ．２０１６１００１３ 网络出版地址：ｈｔｔｐ： ／ ／ ｋｎｓ．ｃｎｋｉ．ｎｅｔ ／ ｋｃｍｓ／ ｄｅｔａｉｌ ／ ２３．１５３８．ｔｐ．２０１７０４０７．１７５８．０２０．ｈｔｍｌ 基于系统动力学模型的物元相关网研究 李文军１，２ ，杨春燕１，２ （１．广东工业大学 可拓学与创新方法研究所，广东 广州 ５１０００６； ２．广东工业大学 机电工程学院，广东 广州 ５１０００６） 摘 要：在可拓学相关分析理论中，关键在于确定相关基元的函数关系。 然而，在具体领域中运用的时候，相关函数 的确定往往是比较困难的，也就局限了相关网方法的使用。 文章以物元为研究对象，对物元的相关网进行了研究， 提出了相关网的动力学模型建模方法以及一种在相关函数未知的情况下，基于系统动力学模型的物元相关函数近 似构造方法。 该方法的原理是通过基础数据的收集和分析，在依据相关网建立的动力学模型中按照固定的步骤进 行模拟分析，得出物元的近似相关函数。 在此基础上，相关分析的进行就变得简单、可模拟。 案例分析的结果表明， 该方法能够有效模拟和近似构造相关物元之间的函数关系，为相关网方法在具体领域中的运用奠定了一定的基础。 关键词：可拓学； 物元； 相关分析； 相关网； 系统动力学； 仿真； 相关函数； 建模 中图分类号：ＴＰ１８ 文献标志码：Ａ 文章编号：１６７３－４７８５（２０１７）０４－０４５９－０９ 中文引用格式：李文军，杨春燕．基于系统动力学模型的物元相关网研究［Ｊ］． 智能系统学报， ２０１７， １２（４）： ４５９－４６７． 英文引用格式：ＬＩ Ｗｅｎｊｕｎ， ＹＡＮＧ Ｃｈｕｎｙａｎ． Ｒｅｓｅａｒｃｈ ｏｎ ａ ｃｏｒｒｅｌａｔｉｖｅ ｎｅｔｗｏｒｋ ｏｆ ｍａｔｔｅｒ⁃ｅｌｅｍｅｎｔｓ ｂａｓｅｄ ｏｎ ａ ｓｙｓｔｅｍ ｄｙｎａｍｉｃｓ ｍｏｄｅｌ［Ｊ］． ＣＡＡＩ ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ ｉｎｔｅｌｌｉｇｅｎｔ ｓｙｓｔｅｍｓ， ２０１７， １２（４）： ４５９－４６７． Ｒｅｓｅａｒｃｈ ｏｎ ａ ｃｏｒｒｅｌａｔｉｖｅ ｎｅｔｗｏｒｋ ｏｆ ｍａｔｔｅｒ⁃ｅｌｅｍｅｎｔｓ ｂａｓｅｄ ｏｎ ａ ｓｙｓｔｅｍ ｄｙｎａｍｉｃｓ ｍｏｄｅｌ ＬＩ Ｗｅｎｊｕｎ １，２ ， ＹＡＮＧ Ｃｈｕｎｙａｎ １，２ （１． Ｒｅｓｅａｒｃｈ Ｉｎｓｔｉｔｕｔｅ ｏｆ Ｅｘｔｅｎｉｃｓ ａｎｄ Ｉｎｎｏｖａｔｉｏｎ Ｍｅｔｈｏｄｓ， Ｇｕａｎｇｄｏｎｇ Ｕｎｉｖｅｒｓｉｔｙ ｏｆ Ｔｅｃｈｎｏｌｏｇｙ， Ｇｕａｎｇｚｈｏｕ ５１０００６， Ｃｈｉｎａ； ２． Ｓｃｈｏｏｌ ｏｆ Ｅｌｅｃｔｒｏｍｅｃｈａｎｉｃａｌ Ｅｎｇｉｎｅｅｒｉｎｇ， Ｇｕａｎｇｄｏｎｇ Ｕｎｉｖｅｒｓｉｔｙ ｏｆ Ｔｅｃｈｎｏｌｏｇｙ， Ｇｕａｎｇｚｈｏｕ ５１０００６， Ｃｈｉｎａ） Ａｂｓｔｒａｃｔ：Ｉｎ ｔｈｅ ｃｏｒｒｅｌａｔｉｖｅ ａｎａｌｙｓｉｓ ｏｆ Ｅｘｔｅｎｉｃｓ， ｔｈｅ ｋｅｙ ｉｓ ｔｏ ｄｅｆｉｎｅ ｔｈｅ ｃｏｒｒｅｌａｔｉｏｎ ｆｕｎｃｔｉｏｎ ｒｅｌａｔｉｎｇ ｔｏ ｔｈｅ ｂａｓｉｃ⁃ ｅｌｅｍｅｎｔｓ． Ｈｏｗｅｖｅｒ， ｉｔ ｉｓ ｖｅｒｙ ｄｉｆｆｉｃｕｌｔ ｔｏ ｄｅｆｉｎｅ ｔｈｅ ｃｏｒｒｅｌａｔｉｏｎ ｆｕｎｃｔｉｏｎ ｗｈｅｎ ｉｔ ｉｓ ａｐｐｌｉｅｄ ｔｏ ｓｐｅｃｉｆｉｃ ａｒｅａｓ ａｎｄ ｔｈｉｓ ｌｉｍｉｔｓ ｔｈｅ ｕｓａｇｅ ｏｆ ｔｈｅ ｃｏｒｒｅｌａｔｉｖｅ ｎｅｔｗｏｒｋ． Ｉｎ ｔｈｉｓ ｐａｐｅｒ， ａ ｃｏｒｒｅｌａｔｉｏｎ ｎｅｔｗｏｒｋ ｂａｓｅｄ ｏｎ ｍａｔｔｅｒ⁃ｅｌｅｍｅｎｔｓ ｉｓ ｓｔｕｄｉｅｄ． Ｔｈｅｎ， ｗｅ ｐｒｅｓｅｎｔ ａ ｍｅｔｈｏｄ ｆｏｒ ｅｓｔａｂｌｉｓｈｉｎｇ ａ ｓｙｓｔｅｍ ｄｙｎａｍｉｃｓ ｍｏｄｅｌ ｏｆ ｔｈｅ ｃｏｒｒｅｌａｔｉｏｎ ｎｅｔｗｏｒｋ ａｎｄ ａ ｍｅｔｈｏｄ ｆｏｒ ａｐｐｒｏｘｉｍａｔｅｌｙ ｉｄｅｎｔｉｆｙｉｎｇ ｔｈｅ ｃｏｒｒｅｌａｔｉｏｎ ｆｕｎｃｔｉｏｎ ｂａｓｅｄ ｏｎ ｔｈｅ ｓｙｓｔｅｍ ｄｙｎａｍｉｃｓ ｍｏｄｅｌ， ｉｎ ｗｈｉｃｈ ｔｈｅ ｃｏｒｒｅｌａｔｉｏｎ ｆｕｎｃｔｉｏｎｓ ｕｎｄｅｒ ｓｏｍｅ ｒｅｌａｔｅｄ ｍａｔｔｅｒ⁃ｅｌｅｍｅｎｔｓ ａｒｅ ｕｎｋｎｏｗｎ． Ｔｈｅ ｐｒｉｎｃｉｐｌｅ ｏｆ ｔｈｉｓ ｍｅｔｈｏｄ ｉｓ ｔｏ ｄｅｒｉｖｅ ｔｈｅ ａｐｐｒｏｘｉｍａｔｅ ｃｏｒｒｅｌａｔｉｏｎ ｆｕｎｃｔｉｏｎｓ ｏｆ ｒｅｌａｔｅｄ ｍａｔｔｅｒ⁃ｅｌｅｍｅｎｔｓ ａｃｃｏｒｄｉｎｇ ｔｏ ｔｈｅ ｐｒｉｎｃｉｐｌｅ ｏｆ ｃｏｌｌｅｃｔｉｎｇ ａｎｄ ａｎａｌｙｚｉｎｇ ｂａｓｉｃ ｄａｔａ， ａｎｄ ｅｓｔａｂｌｉｓｈｉｎｇ ａ ｋｉｎｅｔｉｃ ｍｏｄｅｌ ｆｏｒ ｓｉｍｕｌａｔｉｏｎ ａｎｄ ａｎａｌｙｓｉｓ ｉｎ ｔｅｒｍｓ ｏｆ ａ ｆｉｘｅｄ ｐｒｏｃｅｄｕｒｅ ｉｎ ｔｈｅ ｃｏｒｒｅｌａｔｉｖｅ ｎｅｔｗｏｒｋ． Ｉｎ ｔｈｉｓ ｗａｙ， ｃｏｒｒｅｌａｔｉｖｅ ａｎａｌｙｓｉｓ ｂｅｃｏｍｅｓ ｅａｓｙ ａｎｄ ｃａｎ ｂｅ ｓｉｍｕｌａｔｅｄ． Ｔｈｅ ｃｌｅａｒ ｃｏｎｃｌｕｓｉｏｎ ｉｓ ｔｈａｔ ｔｈｅ ｍｅｔｈｏｄ ｅｆｆｉｃｉｅｎｔｌｙ ｓｉｍｕｌａｔｅｓ ｔｈｅ ｃｏｒｒｅｌａｔｉｏｎ ｆｕｎｃｔｉｏｎ ａｎｄ ｌａｙｓ ｔｈｅ ｆｏｕｎｄａｔｉｏｎ ｆｏｒ ｔｈｅ ａｐｐｌｉｃａｔｉｏｎ ｏｆ ｃｏｒｒｅｌａｔｉｏｎ ａｎａｌｙｓｉｓ ｔｏ ｓｐｅｃｉｆｉｃ ａｒｅａｓ． Ｋｅｙｗｏｒｄｓ： Ｅｘｔｅｎｉｃｓ； ｍａｔｔｅｒ⁃ｅｌｅｍｅｎｔ； ｃｏｒｒｅｌａｔｉｖｅ ａｎａｌｙｓｉｓ； ｃｏｒｒｅｌａｔｉｖｅ ｎｅｔｗｏｒｋ； ｓｙｓｔｅｍ ｄｙｎａｍｉｃｓ； ｓｉｍｕｌａｔｉｏｎ； ｃｏｒｒｅｌａｔｉｏｎ ｆｕｎｃｔｉｏｎｓ； ｍｏｄｅｌｉｎｇ 收稿日期：２０１６－１０－１３． 网络出版日期：２０１７－０４－０７． 基金项目：国家自然科学基金项目（ ６１２７３３０６）；广东省科技计划项目 （２０１６Ａ０４０４０４０１５）． 通信作者：杨春燕． Ｅ⁃ｍａｉｌ： ２７６５１９１０６＠ ｑｑ．ｃｏｍ． 相关网方法是可拓学中建立的利用基元模型 研究基元之间的相关关系的方法［１］ 。 目前对于复 杂系统下相关网的量化研究较少，而对于复杂系统 的研究而言，相关分析是一个很有用的分析方法。 文献［２］研究了复杂系统下相关分析中不同相关特 征量值之间的函数关系，为复杂系统中相关网的进 一步研究打下了坚实的基础。 文献［３－７］基于基元 的相关性介绍了传导变换的概念以及传导效应的 计算方法。 然而，对于复杂系统的相关网，如果能 用更简单系统化的方法进行分析和研究，为相关函 数的近似构造提供依据，将会为可拓创意的生成和

·460. 智能系统学报 第12卷 优选提供现实依据。 态量，(t)为时刻t,的状态量，△为状态变化量。 系统动力学是由美国麻省理工学院J.W. 该物元的特征c可以是“速率”或“辅助变量”，也可 Forrester教授提出的一种对社会经济问题进行系统 以是其他特征。 分析的方法论和定性与定量相结合的分析方法。 本文基于系统动力学模型和可拓学中的相关 其目的在于综合控制论、信息论和决策论的成果， 分析理论，针对一维物元，提出了建立物元相关网 以计算机为工具，分析研究信息反馈系统的结构和 的一种方法，初步确定了本方法的使用步骤，并说 行为。系统动力学研究的是组成系统的内部若干 明其应用领域。在此基础上运用系统动力学理论 因素相互间的影响，并加以模拟分析，得出最优的 对相关函数进行近似构造。案例分析说明了相关 决策，使系统更加完善或者更好地发挥系统的功 网方法与系统动力学进行结合的可行性以及该方 能。当然，这里的系统指的是对于分析的问题所建 法的优点。 立的模型。文献[8-13]对近年来系统动力学的广 泛运用领域进行了综述，并且可以得出系统动力学 1相关分析与系统动力学建模 作为一种系统的科学分析方法，实践证明其在各种 1.1相关分析理论 领域的应用研究效果显著，在很多领域都具有很高 为了让人们更清晰、直观地了解事物之间的相 的应用价值。 关关系和相互作用的关系，可拓学中研究了相关分 可拓学中相关分析理论虽然比较直观地表述 析理论。相关分析是根据物、事和关系之间的相关 了各相关基元相关特征的量值之间的函数关系，但 性，利用基元作为形式化工具，对基元与基元之间 需要依赖于已有领域知识确定函数关系。根据文 的相关关系进行的形式化定量化分析。 献[14-19]可知，如果缺乏领域知识，目前有两种处 基元描述了事物所有的特征及其相应的量值， 理方法：1)如果有相关的数据积累，则可以利用数 如果没有目的性地进行相关分析，则分析工作难以 据挖掘方法或统计方法获得规则知识：2)如果没有 展开，同时工作量也异常大。而其中大部分的工作 相关的数据积累，则只能用规则表示，不能定量地 都是无用功。所以需要根据要分析的目标，选取与 准确表示出来，也就不可能将相关影响过程用函数 其相关基元中的相关特征进行分析，将不相关的特 进行模拟。文献[20]有效利用系统动力学进行数 征摒弃，从而使分析工作简单高效。本文仅以物元 据挖掘工作，取得了很好的效果。 作为研究对象。 在分析时如果能直接通过将可拓学中相关分 文献[1]给出了基元相关的一般定义和相关分 析和系统动力学有机结合，对相关分析而言，就可 析原理。本文重点研究动态物元的相关，对动态物 以使相关网能够进行时间连续的动态仿真模拟，得 元而言，常用的相关关系包括同物异特征物元相 出更加全面准确的分析，为生成更有价值、更准确 关、异物同特征物元相关和异物异特征物元相关。 的决策方案提供依据。 定义对于动态物元M1(t)=(0,(t),c1, 从系统动力学模型的组成部分来说，包括“流” ,(t)),M2(t)=(02(t),c2,2(t)),若2(t)=f(1 与“元素”。“流”即为系统内传递的内容：信息或者 实物。“元素”表示系统内全体属性的一个表征量。 (t)),则称物元M(t)与M2(t)是相关的，记作 一般来说，将所有状态变量在某个时刻的取值视为 M,(t)一→M(t)。 系统当时的状态即为状态变量；系统输人作用后在 动态物元的相关具有如下原理： 系统输出端所出现的变量，是属于不可控变量即为 给定物元M(t)=(O(t),c,v(t)),则至少存在 “速率”：“辅助变量”则是一个可以控制的变量，形 一个异物同特征物元M.(t)=(O'(t),c,'(t))或 成系统的输入。 同物异特征物元M(t)=(O(t),c','(t)或异物 可拓学中的相关分析，可以形式化、定量化分 异特征物元M'(t)=(O'(t),c',v'(t)),使M(t)~ 析若干物元之间的相互作用和相互影响。本文研 M(t),或M(t)~M(t),或M(t)~M'(t)。 究的相关网是由具有相关关系的物元组成的网络， 1.2相关网方法 在网络内传递的内容可以是信息，也可以是实物， 在可拓学中，物元可以形式化表示世间万物， 即为“流”。对于由多个动态物元组成的相关网，如 物元之间的相关关系都可以利用可拓学的相关理 果相关网内的每个动态物元都只有一个特征cm,该 论对其进行形式化、定量化地分析。当某个物元并 动态物元可表示为M(t)=(O(t),c,(t))。设该 不能有效地用来研究问题时，可以考虑利用物元之 特征在某一时刻t。的量值为v(t。),且在时刻，有 间的相关关系，采用其他与之相关的物元来研究。 v(t1)=v(to)+△m,此时，称v(to)为时刻to处的状 另外，一个物元某个特征的量值发生变化，必将导

优选提供现实依据。 系统 动 力 学 是 由 美 国 麻 省 理 工 学 院 Ｊ． Ｗ． Ｆｏｒｒｅｓｔｅｒ 教授提出的一种对社会经济问题进行系统 分析的方法论和定性与定量相结合的分析方法。 其目的在于综合控制论、信息论和决策论的成果， 以计算机为工具，分析研究信息反馈系统的结构和 行为。 系统动力学研究的是组成系统的内部若干 因素相互间的影响，并加以模拟分析，得出最优的 决策，使系统更加完善或者更好地发挥系统的功 能。 当然，这里的系统指的是对于分析的问题所建 立的模型。 文献［８－１３］对近年来系统动力学的广 泛运用领域进行了综述，并且可以得出系统动力学 作为一种系统的科学分析方法，实践证明其在各种 领域的应用研究效果显著，在很多领域都具有很高 的应用价值。 可拓学中相关分析理论虽然比较直观地表述 了各相关基元相关特征的量值之间的函数关系，但 需要依赖于已有领域知识确定函数关系。 根据文 献［１４－１９］可知，如果缺乏领域知识，目前有两种处 理方法：１）如果有相关的数据积累，则可以利用数 据挖掘方法或统计方法获得规则知识；２）如果没有 相关的数据积累，则只能用规则表示，不能定量地 准确表示出来，也就不可能将相关影响过程用函数 进行模拟。 文献［２０］有效利用系统动力学进行数 据挖掘工作，取得了很好的效果。 在分析时如果能直接通过将可拓学中相关分 析和系统动力学有机结合，对相关分析而言，就可 以使相关网能够进行时间连续的动态仿真模拟，得 出更加全面准确的分析，为生成更有价值、更准确 的决策方案提供依据。 从系统动力学模型的组成部分来说，包括“流” 与“元素”。 “流”即为系统内传递的内容：信息或者 实物。 “元素”表示系统内全体属性的一个表征量。 一般来说，将所有状态变量在某个时刻的取值视为 系统当时的状态即为状态变量；系统输入作用后在 系统输出端所出现的变量，是属于不可控变量即为 “速率”；“辅助变量”则是一个可以控制的变量，形 成系统的输入。 可拓学中的相关分析，可以形式化、定量化分 析若干物元之间的相互作用和相互影响。 本文研 究的相关网是由具有相关关系的物元组成的网络， 在网络内传递的内容可以是信息，也可以是实物， 即为“流”。 对于由多个动态物元组成的相关网，如 果相关网内的每个动态物元都只有一个特征 ｃｍ ，该 动态物元可表示为 Ｍ（ｔ）＝ （Ｏ（ ｔ）， ｃ， ｖ（ ｔ））。 设该 特征在某一时刻 ｔ ０ 的量值为 ｖ（ｔ ０ ），且在时刻 ｔ １ 有 ｖ（ｔ １ ）＝ ｖ （ｔ ０ ）＋Δｖ，此时，称 ｖ （ ｔ ０ ）为时刻 ｔ ０ 处的状 态量，ｖ （ｔ １ ）为时刻 ｔ １的状态量，Δｖ 为状态变化量。 该物元的特征 ｃｍ可以是“速率”或“辅助变量”，也可 以是其他特征。 本文基于系统动力学模型和可拓学中的相关 分析理论，针对一维物元，提出了建立物元相关网 的一种方法，初步确定了本方法的使用步骤，并说 明其应用领域。 在此基础上运用系统动力学理论 对相关函数进行近似构造。 案例分析说明了相关 网方法与系统动力学进行结合的可行性以及该方 法的优点。 １ 相关分析与系统动力学建模 １．１ 相关分析理论 为了让人们更清晰、直观地了解事物之间的相 关关系和相互作用的关系，可拓学中研究了相关分 析理论。 相关分析是根据物、事和关系之间的相关 性，利用基元作为形式化工具，对基元与基元之间 的相关关系进行的形式化定量化分析。 基元描述了事物所有的特征及其相应的量值， 如果没有目的性地进行相关分析，则分析工作难以 展开，同时工作量也异常大。 而其中大部分的工作 都是无用功。 所以需要根据要分析的目标，选取与 其相关基元中的相关特征进行分析，将不相关的特 征摒弃，从而使分析工作简单高效。 本文仅以物元 作为研究对象。 文献［１］给出了基元相关的一般定义和相关分 析原理。 本文重点研究动态物元的相关，对动态物 元而言，常用的相关关系包括同物异特征物元相 关、异物同特征物元相关和异物异特征物元相关。 定义 对于动态物元 Ｍ１ （ ｔ） ＝ （ Ｏ１ （ ｔ）， ｃ１ ， ｖ１（ｔ）），Ｍ２（ｔ） ＝ （Ｏ２ （ ｔ），ｃ２ ，ｖ２ （ ｔ）），若 ｖ２ （ ｔ） ＝ ｆ（ ｖ１ （ｔ）），则称物元 Ｍ１ （ ｔ） 与 Ｍ２ （ ｔ） 是相关的， 记作 Ｍ２（ｔ） ～→Ｍ１（ｔ）。 动态物元的相关具有如下原理： 给定物元 Ｍ（ｔ）＝ （Ｏ（ｔ）， ｃ， ｖ（ｔ）），则至少存在 一个异物同特征物元 Ｍｃ（ｔ）＝ （Ｏ′（ｔ）， ｃ， ｖ′ （ｔ））或 同物异特征物元 Ｍｏ（ｔ）＝ （Ｏ（ ｔ）， ｃ′， ｖ′（ ｔ））或异物 异特征物元 Ｍ′（ｔ）＝ （Ｏ′ （ｔ）， ｃ′，ｖ′ （ｔ）），使 Ｍ（ｔ） ～ Ｍｃ（ｔ），或 Ｍ（ｔ） ～ Ｍｏ（ｔ），或 Ｍ（ｔ） ～ Ｍ′（ｔ）。 １．２ 相关网方法 在可拓学中，物元可以形式化表示世间万物， 物元之间的相关关系都可以利用可拓学的相关理 论对其进行形式化、定量化地分析。 当某个物元并 不能有效地用来研究问题时，可以考虑利用物元之 间的相关关系，采用其他与之相关的物元来研究。 另外，一个物元某个特征的量值发生变化，必将导 ·４６０· 智 能 系 统 学 报 第 １２ 卷

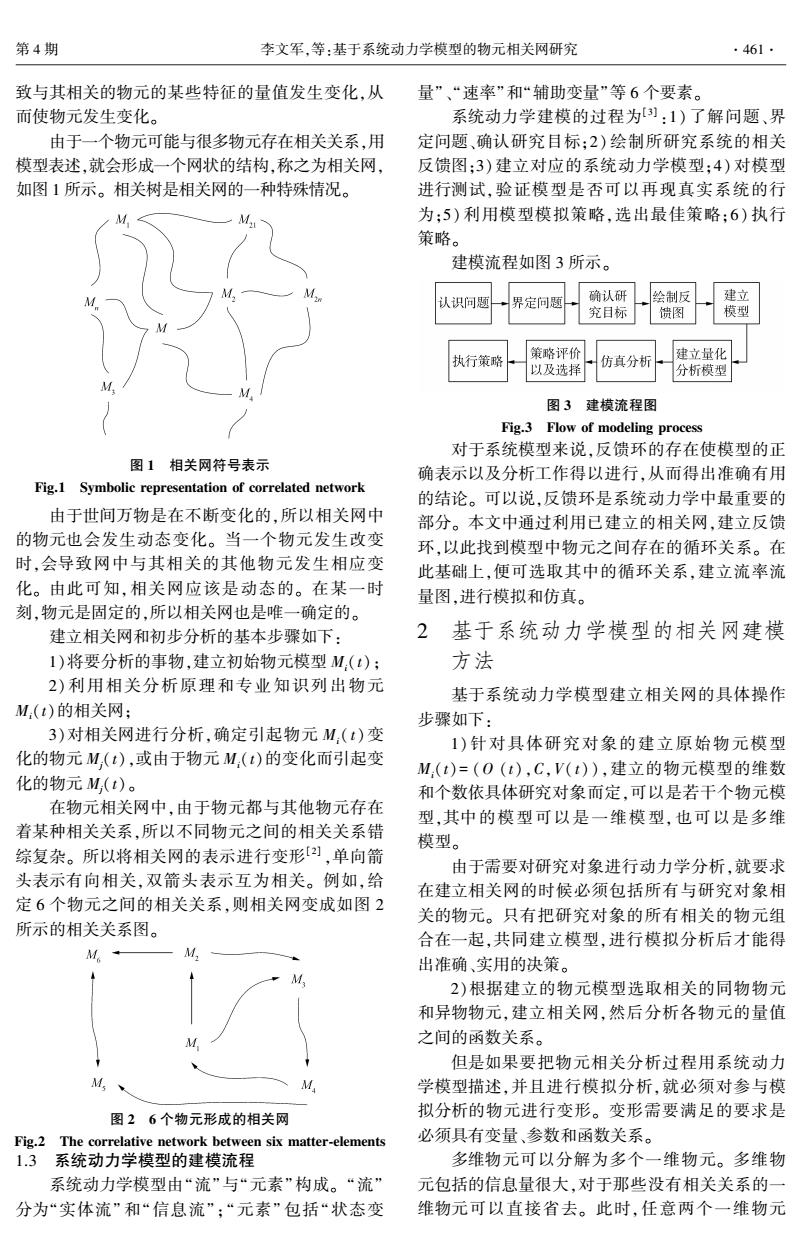
第4期 李文军，等：基于系统动力学模型的物元相关网研究 ·461· 致与其相关的物元的某些特征的量值发生变化，从 量”、“速率”和“辅助变量”等6个要素。 而使物元发生变化。 系统动力学建模的过程为)：1)了解问题、界 由于一个物元可能与很多物元存在相关关系，用 定问题、确认研究目标：2)绘制所研究系统的相关 模型表述，就会形成一个网状的结构，称之为相关网， 反馈图；3)建立对应的系统动力学模型；4)对模型 如图1所示。相关树是相关网的一种特殊情况。 进行测试，验证模型是否可以再现真实系统的行 为：5)利用模型模拟策略，选出最佳策略：6)执行 策略。 建模流程如图3所示。 认识问题 界定问题 确认研 绘制反 建立 究目标 馈图 模型 策路评价 建立量化 执行策略 以及选择 仿真分析 分析模型 图3建模流程图 Fig.3 Flow of modeling process 对于系统模型来说，反馈环的存在使模型的正 图1相关网符号表示 确表示以及分析工作得以进行，从而得出准确有用 Fig.1 Symbolic representation of correlated network 的结论。可以说，反馈环是系统动力学中最重要的 由于世间万物是在不断变化的，所以相关网中 部分。本文中通过利用已建立的相关网，建立反馈 的物元也会发生动态变化。当一个物元发生改变 环，以此找到模型中物元之间存在的循环关系。在 时，会导致网中与其相关的其他物元发生相应变 此基础上，便可选取其中的循环关系，建立流率流 化。由此可知，相关网应该是动态的。在某一时 量图，进行模拟和仿真。 刻，物元是固定的，所以相关网也是唯一确定的。 建立相关网和初步分析的基本步骤如下： 2基于系统动力学模型的相关网建模 1)将要分析的事物，建立初始物元模型M,(t); 方法 2)利用相关分析原理和专业知识列出物元 基于系统动力学模型建立相关网的具体操作 M(t)的相关网： 步骤如下： 3)对相关网进行分析，确定引起物元M,(t)变 1)针对具体研究对象的建立原始物元模型 化的物元M,(t),或由于物元M,(t)的变化而引起变 M,(t)=(O(t),C,V(t)),建立的物元模型的维数 化的物元M(t)。 和个数依具体研究对象而定，可以是若干个物元模 在物元相关网中，由于物元都与其他物元存在 型，其中的模型可以是一维模型，也可以是多维 着某种相关关系，所以不同物元之间的相关关系错 模型。 综复杂。所以将相关网的表示进行变形2]，单向箭 由于需要对研究对象进行动力学分析，就要求 头表示有向相关，双箭头表示互为相关。例如，给 在建立相关网的时候必须包括所有与研究对象相 定6个物元之间的相关关系，则相关网变成如图2 关的物元。只有把研究对象的所有相关的物元组 所示的相关关系图。 合在一起，共同建立模型，进行模拟分析后才能得 M 出准确、实用的决策。 2)根据建立的物元模型选取相关的同物物元 和异物物元，建立相关网，然后分析各物元的量值 之间的函数关系。 但是如果要把物元相关分析过程用系统动力 M M 学模型描述，并且进行模拟分析，就必须对参与模 图26个物元形成的相关网 拟分析的物元进行变形。变形需要满足的要求是 Fig.2 The correlative network between six matter-elements 必须具有变量、参数和函数关系。 1.3系统动力学模型的建模流程 多维物元可以分解为多个一维物元。多维物 系统动力学模型由“流”与“元素”构成。“流” 元包括的信息量很大，对于那些没有相关关系的一 分为“实体流”和“信息流”：“元素”包括“状态变 维物元可以直接省去。此时，任意两个一维物元

致与其相关的物元的某些特征的量值发生变化，从 而使物元发生变化。 由于一个物元可能与很多物元存在相关关系，用 模型表述，就会形成一个网状的结构，称之为相关网， 如图 １ 所示。 相关树是相关网的一种特殊情况。 图 １ 相关网符号表示 Ｆｉｇ．１ Ｓｙｍｂｏｌｉｃ ｒｅｐｒｅｓｅｎｔａｔｉｏｎ ｏｆ ｃｏｒｒｅｌａｔｅｄ ｎｅｔｗｏｒｋ 由于世间万物是在不断变化的，所以相关网中 的物元也会发生动态变化。 当一个物元发生改变 时，会导致网中与其相关的其他物元发生相应变 化。 由此可知，相关网应该是动态的。 在某一时 刻，物元是固定的，所以相关网也是唯一确定的。 建立相关网和初步分析的基本步骤如下： １）将要分析的事物，建立初始物元模型 Ｍｉ（ｔ）； ２）利用相关分析原理和专业知识列出物元 Ｍｉ（ｔ）的相关网； ３）对相关网进行分析，确定引起物元 Ｍｉ（ ｔ）变 化的物元 Ｍｊ（ｔ），或由于物元 Ｍｉ（ｔ）的变化而引起变 化的物元 Ｍｊ（ｔ）。 在物元相关网中，由于物元都与其他物元存在 着某种相关关系，所以不同物元之间的相关关系错 综复杂。 所以将相关网的表示进行变形［２］ ，单向箭 头表示有向相关，双箭头表示互为相关。 例如，给 定 ６ 个物元之间的相关关系，则相关网变成如图 ２ 所示的相关关系图。 图 ２ ６ 个物元形成的相关网 Ｆｉｇ．２ Ｔｈｅ ｃｏｒｒｅｌａｔｉｖｅ ｎｅｔｗｏｒｋ ｂｅｔｗｅｅｎ ｓｉｘ ｍａｔｔｅｒ⁃ｅｌｅｍｅｎｔｓ １．３ 系统动力学模型的建模流程 系统动力学模型由“流”与“元素”构成。 “流” 分为“实体流” 和“信息流”；“元素” 包括“状态变 量”、“速率”和“辅助变量”等 ６ 个要素。 系统动力学建模的过程为［３］ ：１） 了解问题、界 定问题、确认研究目标；２） 绘制所研究系统的相关 反馈图；３）建立对应的系统动力学模型；４） 对模型 进行测试，验证模型是否可以再现真实系统的行 为；５） 利用模型模拟策略，选出最佳策略；６） 执行 策略。 建模流程如图 ３ 所示。 图 ３ 建模流程图 Ｆｉｇ．３ Ｆｌｏｗ ｏｆ ｍｏｄｅｌｉｎｇ ｐｒｏｃｅｓｓ 对于系统模型来说，反馈环的存在使模型的正 确表示以及分析工作得以进行，从而得出准确有用 的结论。 可以说，反馈环是系统动力学中最重要的 部分。 本文中通过利用已建立的相关网，建立反馈 环，以此找到模型中物元之间存在的循环关系。 在 此基础上，便可选取其中的循环关系，建立流率流 量图，进行模拟和仿真。 ２ 基于系统动力学模型的相关网建模 方法 基于系统动力学模型建立相关网的具体操作 步骤如下： １）针对具体研究对象的建立原始物元模型 Ｍｉ（ｔ）＝ （Ｏ （ｔ），Ｃ，Ｖ（ ｔ）），建立的物元模型的维数 和个数依具体研究对象而定，可以是若干个物元模 型，其中的模型可以是一维模型， 也可以是多维 模型。 由于需要对研究对象进行动力学分析，就要求 在建立相关网的时候必须包括所有与研究对象相 关的物元。 只有把研究对象的所有相关的物元组 合在一起，共同建立模型，进行模拟分析后才能得 出准确、实用的决策。 ２）根据建立的物元模型选取相关的同物物元 和异物物元，建立相关网，然后分析各物元的量值 之间的函数关系。 但是如果要把物元相关分析过程用系统动力 学模型描述，并且进行模拟分析，就必须对参与模 拟分析的物元进行变形。 变形需要满足的要求是 必须具有变量、参数和函数关系。 多维物元可以分解为多个一维物元。 多维物 元包括的信息量很大，对于那些没有相关关系的一 维物元可以直接省去。 此时，任意两个一维物元 第 ４ 期 李文军，等：基于系统动力学模型的物元相关网研究 ·４６１·

.462 智能系统学报 第12卷 M,(t)=(0:(t),c:,:(t))和M(t)=(0,(t),S, ,(t))便有了可以进行系统动力学分析的条件，即 变量，(t)、函数关系：(t)=f(y(t)或，(t)= f(,(t))以及函数方程中的参数。 3)建立物元相关网图。相关网是在相关的物 元中表示有关系的符号连起来所组成的网状图形。 但是相关网中并不能表示一个线段的两个端点物 图5动力学相关回路图 元的特征C:和G的量值之间具体的关系：函数关 Fig.5 The correlation loop of dynamics 系、模糊函数关系以及c,与c,两者的量值之间谁是 自变量，谁是因变量等关系。在明确所有相关物元 的量值之间的函数关系的情况下，才能做进一步的 模拟分析。 4)以包含特征c:的一维物元为研究对象，利用 系统动力学软件Venple对相关网图进行变形，称其 为“动力学相关网”。 图6M,的存量流量图 对相关网进行变形的方法：找出相关网中量值 Fig.6 The stock and flow diagram of M 之间具有相关函数关系的物元之间的线段，结合相 互之间自变量与因变量的关系将线段变成有向线 ③量化分析模型及仿真计算。 6)初步得出模拟结果，用于后续的分析。 段，单箭头表示有向相关，双箭头表示互为相关，如 图2。需要注意的是：这里的相关包括同对象异特 利用SD模型的DYNAMO基本方 征相关、异对象同特征相关、异对象异特征相关。 程近似构造相关函数 在此基础上，利用系统动力学软件，将表示互 为相关的双向箭头变成两个单向相关箭头，即相关 3.1SD模型的DYNAMO的基本方程 箭。就变成了动力学相关关系网，如图4。这样做 SD的主要过程之一是通过确定对象系统的水 的目的是为了方便系统动力学建模，所以对相关网 准变量、速率变量、参量、辅助变量等，分析各变量 变形是必要的。 之间存在的函数关系，建立DYNAMO仿真模型，进 行人工计算或者仿真)。这是得到描述系统内部 反馈机制的流程图后建立动力学模型并进行定量 分析的主要工作。DYNAMO方程就是SD的数学模 型或者量化分析模型。 DYNAMO主要采用差分方程式描述有反馈的 社会系统的宏观动态行为，并通过差分及代数方程 式的求解（简单迭代）进行计算机仿真的专用语言。 图4动力学相关关系网 其最大特点是简单明了，容易使用。 Fig.4 The correlation network of dynamics SD的对象系统是随时间变化的动态系统。在 5)结合特征之间的关联传递关系，建立动力学 DYNAMO方程中，变量一般都有时间标号，规定如 模型，并进行模拟分析。 图7。SD使用逐步仿真的方法，仿真的时间步长记 在4)的基础上，整个相关网经过分析、变形已 为DT。 经逐渐走向可以直接建立系统动力学模型的方向。 DT DT ①根据有向线段两端的物元的特征c:和c:之 间的正影响和负影响关系，在线段的箭头处用符号 “+”和“-”标出，调整相关回路，并将回路用符号表 过去 现在 将来 示，如图5。 图7 DYNAMO方程时间标号及其含义 ②建立相关分析目标的存量流量图。 Fig.7 Time label of DYNAMO equation and it's meaning 假设以M,为研究对象，则其对应的存量流量 DYNAMO方程是SD的数学模型或者量化分析 图如图6。 模型。基本的DYNAMO方程主要有以下3个[2)]：

Ｍｉ（ｔ）＝ （Ｏｉ（ ｔ）， ｃｉ， ｖｉ（ ｔ）） 和 Ｍｊ（ ｔ） ＝ （Ｏｊ（ ｔ）， ｃｊ， ｖｊ（ｔ））便有了可以进行系统动力学分析的条件，即 变量 ｖｉ（ ｔ）、函数关系 ｖｉ（ ｔ） ＝ ｆ ｉｊ（ ｖｊ（ ｔ）） 或 ｖｊ（ ｔ） ＝ ｆ ｊｉ（ｖｉ（ｔ））以及函数方程中的参数。 ３）建立物元相关网图。 相关网是在相关的物 元中表示有关系的符号连起来所组成的网状图形。 但是相关网中并不能表示一个线段的两个端点物 元的特征 ｃｉ 和 ｃｊ 的量值之间具体的关系：函数关 系、模糊函数关系以及 ｃｉ 与 ｃｊ 两者的量值之间谁是 自变量，谁是因变量等关系。 在明确所有相关物元 的量值之间的函数关系的情况下，才能做进一步的 模拟分析。 ４）以包含特征 ｃｉ 的一维物元为研究对象，利用 系统动力学软件 Ｖｅｎｐｌｅ 对相关网图进行变形，称其 为“动力学相关网”。 对相关网进行变形的方法：找出相关网中量值 之间具有相关函数关系的物元之间的线段，结合相 互之间自变量与因变量的关系将线段变成有向线 段，单箭头表示有向相关，双箭头表示互为相关，如 图 ２。 需要注意的是：这里的相关包括同对象异特 征相关、异对象同特征相关、异对象异特征相关。 在此基础上，利用系统动力学软件，将表示互 为相关的双向箭头变成两个单向相关箭头，即相关 箭。 就变成了动力学相关关系网，如图 ４。 这样做 的目的是为了方便系统动力学建模，所以对相关网 变形是必要的。 图 ４ 动力学相关关系网 Ｆｉｇ．４ Ｔｈｅ ｃｏｒｒｅｌａｔｉｏｎ ｎｅｔｗｏｒｋ ｏｆ ｄｙｎａｍｉｃｓ ５）结合特征之间的关联传递关系，建立动力学 模型，并进行模拟分析。 在 ４）的基础上，整个相关网经过分析、变形已 经逐渐走向可以直接建立系统动力学模型的方向。 ①根据有向线段两端的物元的特征 ｃｉ 和 ｃｊ 之 间的正影响和负影响关系，在线段的箭头处用符号 “＋”和“－”标出，调整相关回路，并将回路用符号表 示，如图 ５。 ②建立相关分析目标的存量流量图。 假设以 Ｍ４ 为研究对象，则其对应的存量流量 图如图 ６。 图 ５ 动力学相关回路图 Ｆｉｇ．５ Ｔｈｅ ｃｏｒｒｅｌａｔｉｏｎ ｌｏｏｐ ｏｆ ｄｙｎａｍｉｃｓ 图 ６ Ｍ４ 的存量流量图 Ｆｉｇ．６ Ｔｈｅ ｓｔｏｃｋ ａｎｄ ｆｌｏｗ ｄｉａｇｒａｍ ｏｆ Ｍ４ ③量化分析模型及仿真计算。 ６）初步得出模拟结果，用于后续的分析。 ３ 利用 ＳＤ 模型的 ＤＹＮＡＭＯ 基本方 程近似构造相关函数 ３．１ ＳＤ 模型的 ＤＹＮＡＭＯ 的基本方程 ＳＤ 的主要过程之一是通过确定对象系统的水 准变量、速率变量、参量、辅助变量等，分析各变量 之间存在的函数关系，建立 ＤＹＮＡＭＯ 仿真模型，进 行人工计算或者仿真［７］ 。 这是得到描述系统内部 反馈机制的流程图后建立动力学模型并进行定量 分析的主要工作。 ＤＹＮＡＭＯ 方程就是 ＳＤ 的数学模 型或者量化分析模型。 ＤＹＮＡＭＯ 主要采用差分方程式描述有反馈的 社会系统的宏观动态行为，并通过差分及代数方程 式的求解（简单迭代）进行计算机仿真的专用语言。 其最大特点是简单明了，容易使用。 ＳＤ 的对象系统是随时间变化的动态系统。 在 ＤＹＮＡＭＯ 方程中，变量一般都有时间标号，规定如 图 ７。 ＳＤ 使用逐步仿真的方法，仿真的时间步长记 为 ＤＴ。 图 ７ ＤＹＮＡＭＯ 方程时间标号及其含义 Ｆｉｇ．７ Ｔｉｍｅ ｌａｂｅｌ ｏｆ ＤＹＮＡＭＯ ｅｑｕａｔｉｏｎ ａｎｄ ｉｔ’ｓ ｍｅａｎｉｎｇ ＤＹＮＡＭＯ 方程是 ＳＤ 的数学模型或者量化分析 模型。 基本的 ＤＹＮＡＭＯ 方程主要有以下 ３ 个［１２］ ： ·４６２· 智 能 系 统 学 报 第 １２ 卷

第4期 李文军，等：基于系统动力学模型的物元相关网研究 ·463. 1)水准方程。它是计算水准变量的方程，也就 根据物元的构造规范，正确建立研究对象关于其特 是计算一维物元特征量值的方程。它的标准形式为 征和相应的量值构成的多个一维物元。确定相关 LEVELLEVEL,DT (RIN2-ROUT) 的一维物元。 (1) 2)根据领域知识，搜集研究对象关于其特征的 式中：LEVEL,表示过去t1时刻的水准量，即此时一 量值变化的一些数据，需要注意这些数据的变化规 维物元M(1)=(O(t1),c,v(t1)的量值；LEVEL 律。不同的函数曲线代表着不同的函数类型。作 表示现在t2时刻的水准量，即此时一维物元 为佐证确定的相关函数是否符合事实并且可用的 M(2)=(0(t2),c,(t2))的量值；DT表示两个时 依据。 刻1，和t2之间的时间间隔；RIN,表示该时间段内 3)根据SD的基本函数模型，在符合相关数学 量值的增加速率；ROUT,,表示该时间段内量值的减 规则的情况下，尽量从最简单的函数方程出发来近 少的速率。 似构造特征的相关函数。如果上一次确定相关函 2)速率方程。它是计算速率变化量的方程，用 数没有成功的话，根据上一次函数方程模拟得到的 来计算从t,到t,时间段内一维物元特征量值变化 信息作为依据，逐渐将方程复杂化，继续模拟分析， 速率的量值。 直到找到可以描述事实规律的近似相关函数。 RATE·t2L=fL·t2,A·t2,C,…）(2) 4)利用已经建好的相关网动力学模型，在参数 式中：L·t2表示t2时刻的水准量，即一维物元 相同的情况下，对近似构造的函数进行建模仿真， M(t2)的特征c的量值v(t2);A·t2表示t2时刻描 根据搜集的数据，判断函数的正确性，如果不正确， 述水准变量的辅助变量：C为常数。 重复上述操作，直到找到符合实际规律的近似相关 该速率方程并没有标准的形式，根据要分析的 函数。 对象而定。速率的值在DT内不变，速率方程是在 需要补充一点，在有数据支撑的情况下，尽量 2时刻进行计算，而在自t,至t2的时间间隔（即 把相关网建得详细一些，将有助于确定更加准确的 DT)中假定保持不变。 相关函数。 3)辅助方程。它是用来辅助说明速率变量的 根据客观事实，可以确定相关因素并且在数据 方程。 详实的情况下运用本方法比较方便。对于受很多 AUX·42=g(A·2,L·2,R,C,…)(3) 复杂因素影响的物元相关网，该方法并不适合使用。 式中：R,表示在时刻t,和2之间的时间间隔内，一 4 案例分析 维物元M(t)关于特征c的量值v(t)变化的速率。 该辅助方程没有统一的标准格式，有时需要其 W公司是一家数字教学器材公司。VAX系列 他参数方程来进一步说明。 微型计算机是这家公司很成功的产品。每台VAX 另外还有赋值方程和常量方程，本文没有涉 微型计算机的售价在100000~150000美元之间。 及，此不赘述。 VAX11/750型微型计算机于1980年试制成功。其 3.2近似构造相关函数的操作步骤 销售主要是靠用户的口头传播。通过对一定数量 由于SD的基本函数模型已经概括性地刻画了 的数据样本进行分析可知：销售曲线成正态分布， 影响系统的所有相关函数关系，该模型在大多数相 产品累计销售曲线呈现为S型结构。 关领域都是很实用的，也说明了该基本函数模型的 为了让产品的销售过程持续保持良好的状态。 准确性。所以，在进行相关分析时，准确相关函数 下面利用本文提出的方法来研究该新产品的销售 未知的情况下，就可以利用SD的基本函数模型对 过程中与产品的销售相关的因素，并且找寻相互之 该相关关系进行判定，并且进行近似的构造，以便 间的相关函数。对于企业来说，这样就可以细致准 于进行相关分析。同时，为了方便相关分析能够利 确地模拟产品销售过程的各种情况，为进一步做出 用系统建模这个简单的工具进行操作，可以考虑按 正确的决策提供依据，使产品的销售过程满足企业 着系统动力学的规范来操作。这样的好处是能够 的利润诉求。 运用系统动力学的领域，相关网的实际运用就可以 4.1建模与相关分析 拓宽到该领域。具体步骤如下： 1)根据案例背景以及相关资料，建立产品的物 1)近似构造某研究对象的相关关系时，首先要 元模型如下：

１）水准方程。 它是计算水准变量的方程，也就 是计算一维物元特征量值的方程。 它的标准形式为 ＬＥＶＥＬｔ２ ＝ ＬＥＶＥＬｔ１ ＋ ＤＴ·（ＲＩＮｔ１ ｔ２ － ＲＯＵＴｔ１ ｔ２ ） （１） 式中：ＬＥＶＥＬｔ１表示过去 ｔ １ 时刻的水准量，即此时一 维物元 Ｍ（ｔ １ ）＝ （Ｏ（ｔ １ ）， ｃ， ｖ（ｔ １ ））的量值；ＬＥＶＥＬｔ２ 表 示 现 在 ｔ ２ 时 刻 的 水 准 量， 即 此 时 一 维 物 元 Ｍ（ｔ ２ ）＝ （Ｏ（ｔ ２ ）， ｃ， ｖ（ｔ ２ ））的量值；ＤＴ 表示两个时 刻 ｔ １ 和 ｔ ２ 之间的时间间隔；ＲＩＮｔ１ ｔ２表示该时间段内 量值的增加速率；ＲＯＵＴｔ１ ｔ２表示该时间段内量值的减 少的速率。 ２）速率方程。 它是计算速率变化量的方程，用 来计算从 ｔ １ 到 ｔ ２ 时间段内一维物元特征量值变化 速率的量值。 ＲＡＴＥ·ｔ ２ Ｌ ＝ ｆ（Ｌ·ｔ ２ ， Ａ·ｔ ２ ，Ｃ，…） （２） 式中： Ｌ · ｔ ２ 表示 ｔ ２ 时刻的水准量， 即一维物元 Ｍ（ｔ ２ ）的特征 ｃ 的量值 ｖ（ ｔ ２ ）；Ａ·ｔ ２ 表示 ｔ ２ 时刻描 述水准变量的辅助变量；Ｃ 为常数。 该速率方程并没有标准的形式，根据要分析的 对象而定。 速率的值在 ＤＴ 内不变，速率方程是在 ｔ ２ 时刻进行计算，而在自 ｔ １ 至 ｔ ２ 的时间间隔（ 即 ＤＴ）中假定保持不变。 ３）辅助方程。 它是用来辅助说明速率变量的 方程。 ＡＵＸ·ｔ ２ ＝ ｇ（Ａ·ｔ ２ ， Ｌ·ｔ ２ ，Ｒｔ１ ｔ２ ， Ｃ， …） （３） 式中：Ｒｔ１ ｔ２表示在时刻 ｔ １ 和 ｔ ２ 之间的时间间隔内，一 维物元 Ｍ（ｔ）关于特征 ｃ 的量值 ｖ（ｔ）变化的速率。 该辅助方程没有统一的标准格式，有时需要其 他参数方程来进一步说明。 另外还有赋值方程和常量方程，本文没有涉 及，此不赘述。 ３．２ 近似构造相关函数的操作步骤 由于 ＳＤ 的基本函数模型已经概括性地刻画了 影响系统的所有相关函数关系，该模型在大多数相 关领域都是很实用的，也说明了该基本函数模型的 准确性。 所以，在进行相关分析时，准确相关函数 未知的情况下，就可以利用 ＳＤ 的基本函数模型对 该相关关系进行判定，并且进行近似的构造，以便 于进行相关分析。 同时，为了方便相关分析能够利 用系统建模这个简单的工具进行操作，可以考虑按 着系统动力学的规范来操作。 这样的好处是能够 运用系统动力学的领域，相关网的实际运用就可以 拓宽到该领域。 具体步骤如下： １）近似构造某研究对象的相关关系时，首先要 根据物元的构造规范，正确建立研究对象关于其特 征和相应的量值构成的多个一维物元。 确定相关 的一维物元。 ２）根据领域知识，搜集研究对象关于其特征的 量值变化的一些数据，需要注意这些数据的变化规 律。 不同的函数曲线代表着不同的函数类型。 作 为佐证确定的相关函数是否符合事实并且可用的 依据。 ３）根据 ＳＤ 的基本函数模型，在符合相关数学 规则的情况下，尽量从最简单的函数方程出发来近 似构造特征的相关函数。 如果上一次确定相关函 数没有成功的话，根据上一次函数方程模拟得到的 信息作为依据，逐渐将方程复杂化，继续模拟分析， 直到找到可以描述事实规律的近似相关函数。 ４）利用已经建好的相关网动力学模型，在参数 相同的情况下，对近似构造的函数进行建模仿真， 根据搜集的数据，判断函数的正确性，如果不正确， 重复上述操作，直到找到符合实际规律的近似相关 函数。 需要补充一点，在有数据支撑的情况下，尽量 把相关网建得详细一些，将有助于确定更加准确的 相关函数。 根据客观事实，可以确定相关因素并且在数据 详实的情况下运用本方法比较方便。 对于受很多 复杂因素影响的物元相关网，该方法并不适合使用。 ４ 案例分析 Ｗ 公司是一家数字教学器材公司。 ＶＡＸ 系列 微型计算机是这家公司很成功的产品。 每台 ＶＡＸ 微型计算机的售价在 １００ ０００ ～ １５０ ０００ 美元之间。 ＶＡＸ１１ ／ ７５０ 型微型计算机于 １９８０ 年试制成功。 其 销售主要是靠用户的口头传播。 通过对一定数量 的数据样本进行分析可知：销售曲线成正态分布， 产品累计销售曲线呈现为 Ｓ 型结构。 为了让产品的销售过程持续保持良好的状态。 下面利用本文提出的方法来研究该新产品的销售 过程中与产品的销售相关的因素，并且找寻相互之 间的相关函数。 对于企业来说，这样就可以细致准 确地模拟产品销售过程的各种情况，为进一步做出 正确的决策提供依据，使产品的销售过程满足企业 的利润诉求。 ４．１ 建模与相关分析 １）根据案例背景以及相关资料，建立产品的物 元模型如下： 第 ４ 期 李文军，等：基于系统动力学模型的物元相关网研究 ·４６３·