磁矩: dl wo rdr §143磁场的高斯定理和安培环路定理 dp=(a r2l 一、磁通量 =(r r2ordrn dΦm=Bcos0ds p=∫pn =B.d忑 d area rdr +R Φ.=j川on=B 409R 1 单位:Tm2 通俗理解:磁塘量可以理解为通过某曲面磁 力线的条数, 度位厅下■ 官■■ 二、磁场的高斯定理 静电场高斯定理:E,5=∑ql6 中=B6=用∑d5=∑乐画压 包围 稳恒磁场: 月85= =2m.=0 单萨定理:dB=凸×7 4元3 毕萨拉定理:B=凸M×7 4πr3 ldi Idh,Idl. dΦm=0 Idlldl d地.=0 dB,dB. dB.dB... 地m1,d地2→地l=d地2=…=d帅y=0 dΦ,dΦn2.tl=dn2=…=d地v=0 ■位≤■■■■■ ■■■■■■■看 6
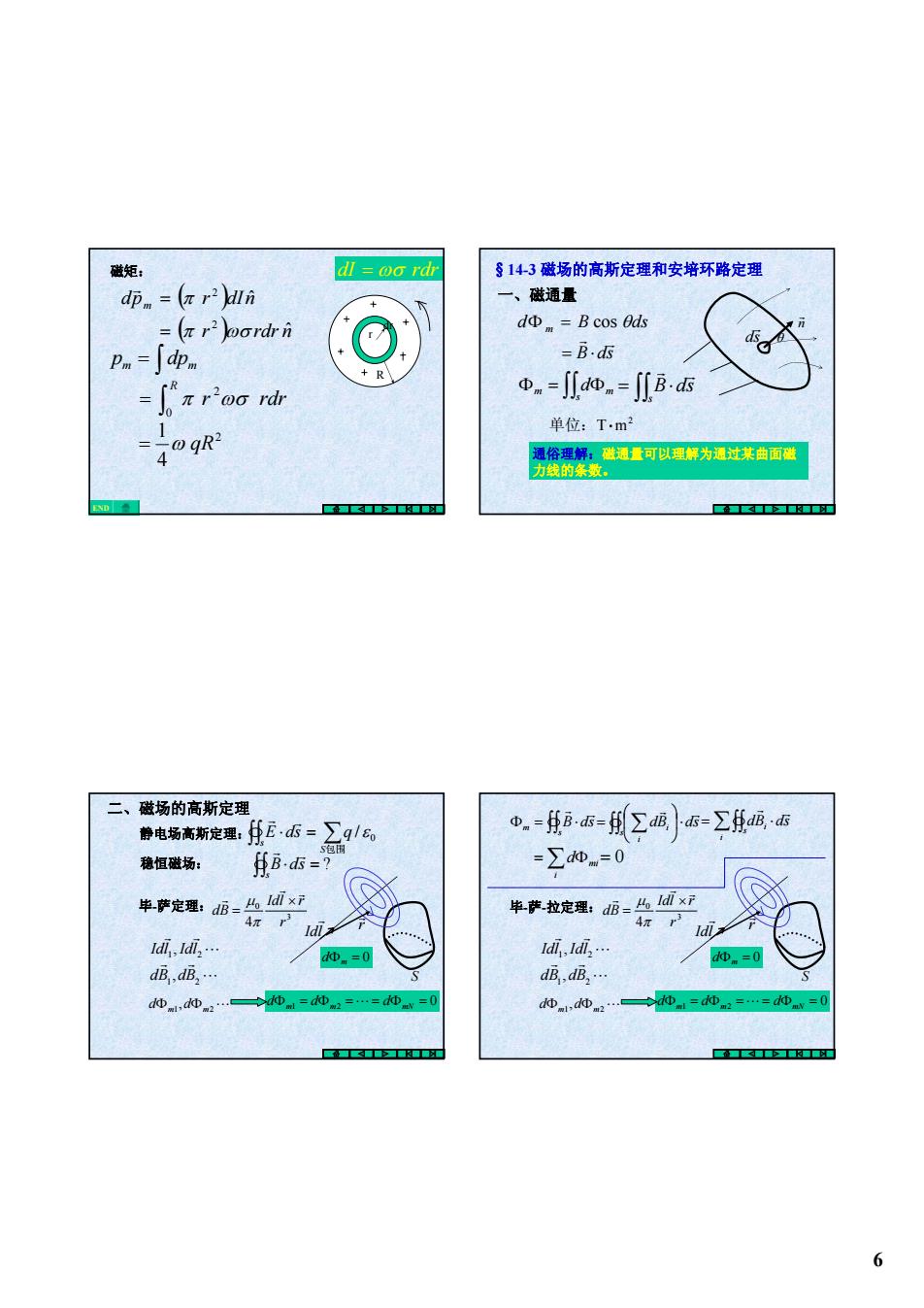
6 dp ( r )dI n m ˆ 2 = π r ∫ m = m p dp 磁矩: R r dr r rdr R 0 2 π ωσ ∫ = 2 4 1 = ω qR END dI = ωσ rdr ( r ) rdr nˆ 2 = π ωσ §14-3 磁场的高斯定理和安培环路定理 一、磁通量 ds r θ n r d B ds Φ m = cos θ Φ = ∫∫ Φs m m d 2 单位:T⋅ m ∫∫ = ⋅ s B ds r r B ds r r = ⋅ 通俗理解:磁通量可以理解为通过某曲面磁 力线的条数。 静电场高斯定理:∫∫s ⋅ = ∑S E ds q 包围 0 / ε r r ∫∫ ⋅ = s B ds ? r r 二、磁场的高斯定理 稳恒磁场: 毕-萨定理: 3 0 4 r Idl r dB r r r × = π μ L r r 1 2 Idl ,Idl L r r 1 2 dB ,dB dΦm1, dΦm2L 0 dΦm1 = dΦm2 =L= dΦmN = dΦm = 0 Idl r S r r ∫∫ Φ = ⋅ s m B ds r r ∫∫ ∑ ⎟⋅ ⎠ ⎞ ⎜ ⎝ ⎛ = s i i dB ds r r ∑∫∫ = ⋅ i s i dB ds r r 毕-萨-拉定理: 3 0 4 r Idl r dB r r r × = π μ L r r 1 2 Idl ,Idl L r r 1 2 dB ,dB dΦm1, dΦm2L 0 dΦm1 = dΦm2 =L= dΦmN = dΦm = 0 Idl r S r r = ∑ Φ i mi d = 0

中=fBds=∑瓜6=∑f通函 三、安培环路定理 =∑mm=0 B.s=0 静电场: E.di=0 无旋场 E.ds=qleo fB.6=0 静磁场: BB-dl≠0 有旋场 E线出自正电荷, 线无头无尾 若任选一根磁力线为闭合回路 止于负电荷 有源场! 无源场! B.di=fBdl≠0 反映自然界无磁单极的事实 度位厅下■ ■合■■■■ 1、回路包围电流 2、回路不包围电流 2 fB.di=fBrdo B.di=Brdo fB-d7-Bd -绘p-岩o= =Bnido+[B.ndo 注:若1绕向相反或电流反向 ∮Bdi=-hl dedo = 当磁第方向与识分跻经前罐疗方向崩成右 手凯龙关亮时电宽为正,反之为负。 22o-1dp-05袋米 ■位≤■■■■■ ■■■■■■■ 7
7 ∫∫ ⋅ = s E ds q 0 / ε r r 止于负电荷 E线出自正电荷, r B线无头无尾 r 有源场! 无源场! 反映自然界无磁单极的事实?! ∫∫ ⋅ = s B ds 0 r r ∫∫ ⋅ = s B ds 0 r r ∫∫ Φ = ⋅ s m B ds r r ∫∫ ∑ ⎟⋅ ⎠ ⎞ ⎜ ⎝ ⎛ = s i i dB ds r r ∑∫∫ = ⋅ i s i dB ds r r = ∑ Φ i mi d = 0 三、安培环路定理 静电场: ∫ ⋅ = l E dl 0 r r 静磁场: ??? ∫ ⋅ = l B dl r r 无旋场 ??? 有旋场 若任选一根磁力线为闭合回路 ∫ ⋅ l B dl r r ≠ 0 ∫ = l Bdl ⋅ ≠ 0 ∫l B dl r r I dl r r r dϕ l B r ϕ π μ e r I B r r 2 0 = B⋅ dl = Brdϕ r r 1、回路包围电流 ∫ ⋅ l B dl r r 注:若 l 绕向相反或电流反向 ⋅ = ? ∫l B dl r r ϕ π μ rd r I ∫l = 2 0 I = μ0 B dl I l = −μ0 ⋅ ∫ r r ∫ = l d I ϕ π μ 2 0 ∫ = l Brdϕ 当电流方向与积分路径的绕行方向构成右 手螺旋关系时电流为正,反之为负。 2、回路不包围电流 d 1 d 1 2 d 2 1 2 B l B l B l l l l r r r r r r ⋅ = ⋅ + ⋅ ∫ ∫ ∫ 1 dl r 2 dl r B1 r B2 r 1 l 2l ( d d ) 2 1 2 0 ∫ ∫ = + l l I ϕ ϕ π μ = 0 I ∫ = 1 1 1d l B r ϕ ∫ + 2 2 2d l B r ϕ ( d d ) 与绕向无关! 2 1 2 0 ∫ ∫− = − l l I ϕ ϕ π μ