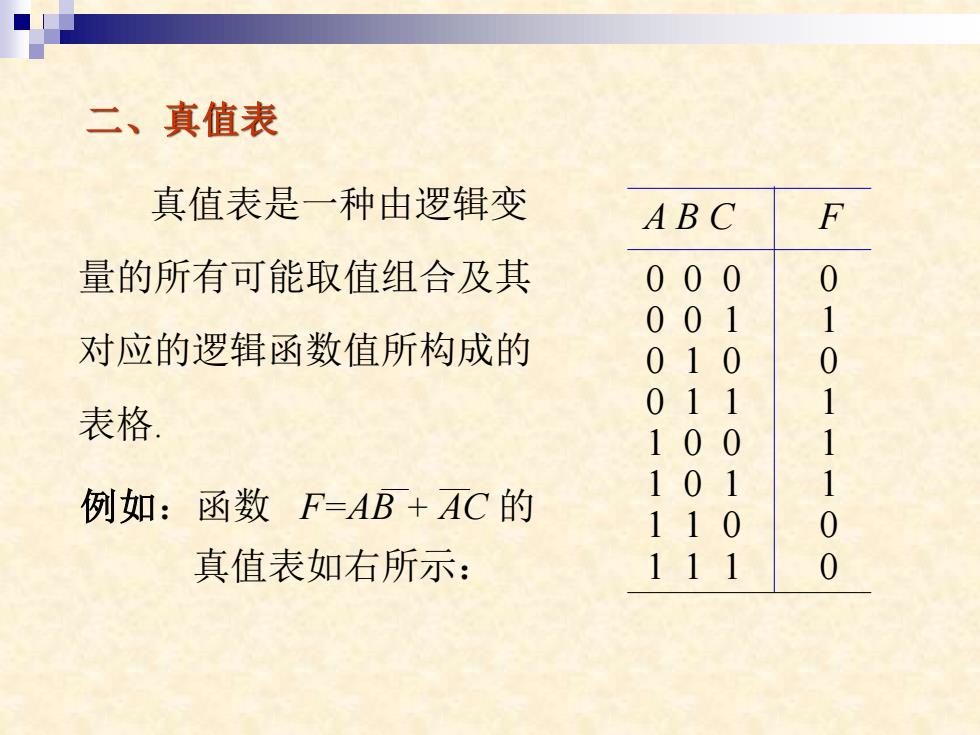
二、真值表 真值表是一种由逻辑变 ABC F 量的所有可能取值组合及其 000 0 001 1 对应的逻辑函数值所构成的 010 0 表格。 011 1 100 1 例如:函数F=AB+AC的 101 1 110 0 真值表如右所示: 111 0
二、真值表 真值表是一种由逻辑变 量的所有可能取值组合及其 对应的逻辑函数值所构成的 表格. 例如:函数 F=AB + AC 的 真值表如右所示: A B C F 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 0 1 1 1 0

三、卡诺图 卡诺图是一种用图形描述逻辑函数的方法
三、卡诺图 卡诺图是一种用图形描述逻辑函数的方法

2.2.12.2 逻辑代数的基本定理和规则 2.2.1基本定理 定理1 0+0=0 1+0=1 0+1=1 1+1=1 0.0=0 1.0=0 0·1=0 1·1=1 推论:1=0 0=1
2.2 逻辑代数的基本定理和规则 2.2.1 基本定理 定理1 0+0=0 1+0=1 0+1=1 1+1=1 0 0 =0 1 0 =0 0 1 =0 1 1 =1 推论: 1 = 0 0 = 1 2.2.1

定理2(重叠律) A十A=A A·A=A 定理3(吸收律) A十A·B=A 4(4+B)=4 定理4(吸收律) A十A·B=A+BA(A+B)=A·B 定理5(对合律)万=A 定理6(德摩根定理)A+B=A十BA·B=不十B 定理7AB+AB=A (A+B)(A+B)=A 定理8(包含律)AB+AC+BC=AB+不.C
定理2(重叠律) A+A=A A A =A 定理3(吸收律) A+A B=A A ( A +B)=A 定理4(吸收律) A+A B=A+B A ( A +B)=A B 定理5(对合律) A=A 定理6(德摩根定理)A+B=A+B A B =A+B 定理7 AB+AB=A (A+B)(A+B)=A 定理8(包含律) AB+AC+BC=AB+AC

2.2.2逻辑代数的重要规则 2.2.2 代入规则 任何一个含有变量A的逻辑等式,如果将 所有出现A的位置都代之以同一个逻辑函数F, 则等式仍然成立。 例如:给定逻辑等式A(B+C)=AB+AC,若 用A+BC代替A,则该等式仍然成立,即 (A+BC)(B+C)-(4+BC)B+(A+BC)C 由公理5(A+A=1)同样有等式 f(A1 A2..An)+f(A1,A2....,An)=1
f (A1 , A2 , …, An )+f (A1 , A2 , …, An )=1 2.2.2 逻辑代数的重要规则 一、代入规则 任何一个含有变量A的逻辑等式,如果将 所有出现A的位置都代之以同一个逻辑函数F, 则等式仍然成立。 例如:给定逻辑等式A(B+C)=AB+AC,若 用A+BC代替A,则该等式仍然成立,即: (A+BC)(B+C)=(A+BC)B+(A+BC)C 由公理5(A+A=1)同样有等式 2.2.2