2.二重极限不存在的例子 2 t= x2+y2,(比,月≠(0,0) y 点P(x,y)沿直线y=x →(0,0)时,有 k lim y 0x2+2 1+k2 V=0 故imf(x,y)不存在 x→0 '→0 y=kx 那么,曲面在点0,0)附近 的形状是怎样的呢? 曲面与z轴无交点; 曲面关于平面y=x对称; 曲面关于平面y=-x对称; 合
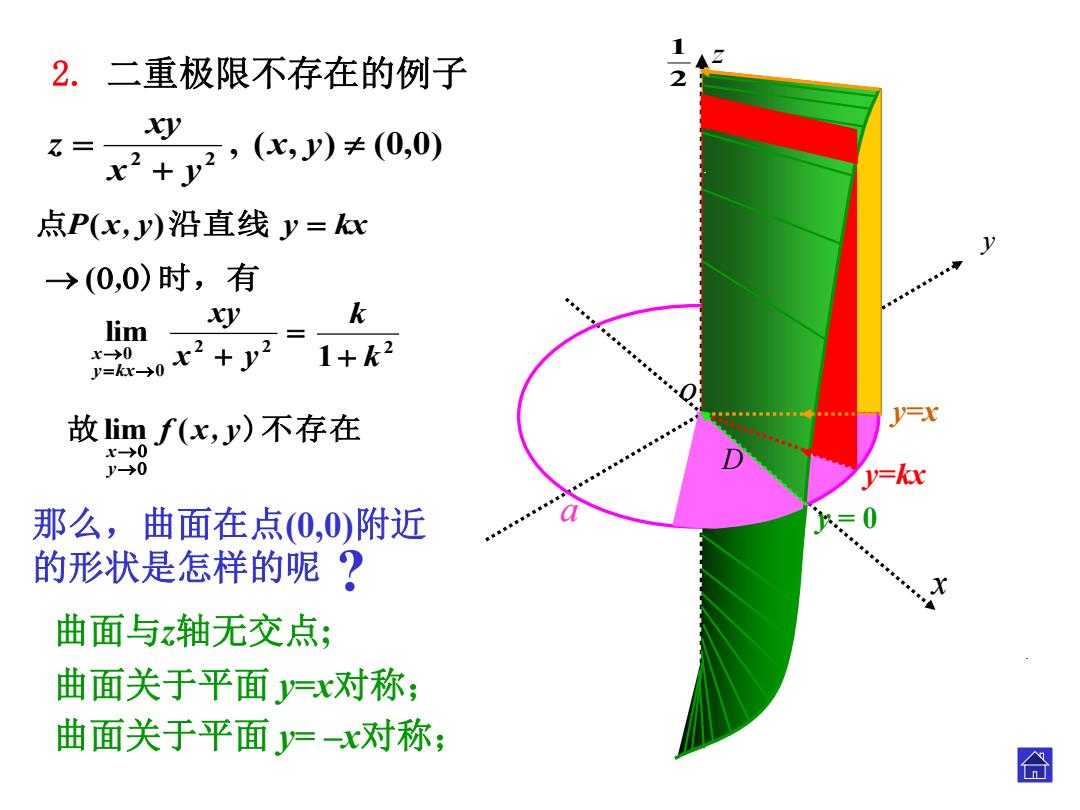
o x y , ( , ) (0,0) 2 2 x y x y xy z y=kx y=x 2 1 z a . D . 那么,曲面在点(0,0)附近 的形状是怎样的呢 ? 曲面与z轴无交点; 曲面关于平面 y=x对称; 曲面关于平面 y= –x对称; y = 0 . 点P(x, y)沿直线 y kx 故 f x, y)不存在 y x lim ( 2 2 0 0 lim x y xy y kx x 2 1 k k (,)时,有 2. 二重极限不存在的例子

2.二重极限不存在的例子 1-2 t= x2+y2,(化月≠(0,0) y 1+k2 点P(x,y)沿直线y=x →(0,0)时,有 k lim y 02+2 1+k2 故imf(x,y)不存在 x→0 '→0 y=kx 那么,曲面在点0,0)附近 的形状是怎样的呢? 曲面与z轴无交点; 曲面关于平面y=x对称; 曲面关于平面y=-x对称; 合
o x y , ( , ) (0,0) 2 2 x y x y xy z y=kx y=x 2 1 k k 2 1 z a y= – x 2 1 . D . 那么,曲面在点(0,0)附近 的形状是怎样的呢 ? 曲面与z轴无交点; 曲面关于平面 y=x对称; 曲面关于平面 y= –x对称; . y = 0 . 点P(x, y)沿直线 y kx 故 f x, y)不存在 y x lim ( 2 2 0 0 lim x y xy y kx x 2 1 k k (,)时,有 2. 二重极限不存在的例子