
6.2 Composite hypothesis testing Composite hypothesis test:Detection of signal with random parameter.(Simple hypothesis test) =a vector of random parameters associated with hypothesis Ho :a vector of random parameters associated with hypothesis H m≠n UESTC 6
6 UESTC 6.2 Composite hypothesis testing 0 01 0 { , , } = m : a vector of random parameters associated with hypothesis H0 1 11 1 { , , } = n : a vector of random parameters associated with hypothesis H1 • Composite hypothesis test: Detection of signal with random parameter. (Simple hypothesis test) m n

Assume the complex measurements represented as y=Sg+zj,i=0,1,j=1,…,k (6.5) It follows that the conditional probabilities are py|B)=p(y,y2,…yk|H,B1,…,fm)(6.6 p,y川B)=p(y,y2,…yk|H,B1,…,m)(6.7) Given the set of measurements,we want to decide on a hypothesis. UESTC 7
7 UESTC It follows that the conditional probabilities are Given the set of measurements, we want to decide on a hypothesis. 0 0 1 2 0 01 0 ( | ) ( , , | , , , ) (6.6) k m p y p y y y H = 1 1 1 2 1 11 1 ( | ) ( , , | , , , ) (6.7) p y p y y y H = k n Assume the complex measurements represented as , 0,1, 1, , (6.5) j ij j y s z i j k = + = =

6.2.1 Known density functions Consider the costs are functions of random parameters,the average risk can be written as r=πo+πi =元jJp,GB,)p(E,)Cw(E,)dE,d→PCo +rJP)(B)Cn(B.)dBdy +zJ五p,川E,p(E,)Cn(B,)aB,d +πJp(川E,)p(B,)C(E,)aB,d (6.8) JES
6.2.1 Known density functions Consider the costs are functions of random parameters, the average risk can be written as 8 UESTC 1 0 0 1 1 0 0 0 0 1 0 0 0 10 0 0 0 0 1 1 01 1 1 1 1 1 1 1 1 1 0 00 0 0 0 0 0 0 0 0 1 1 0 1 ( | ) ( ) ( ) ( | ) ( ) ( | ) ( ) ( ) ( | ) ( ) ) ( ( R R R R p y p C d d r p y p C d d y p y p C d d y p r C r y y p P C = + = + + → + 1 ) (6.8) d d y
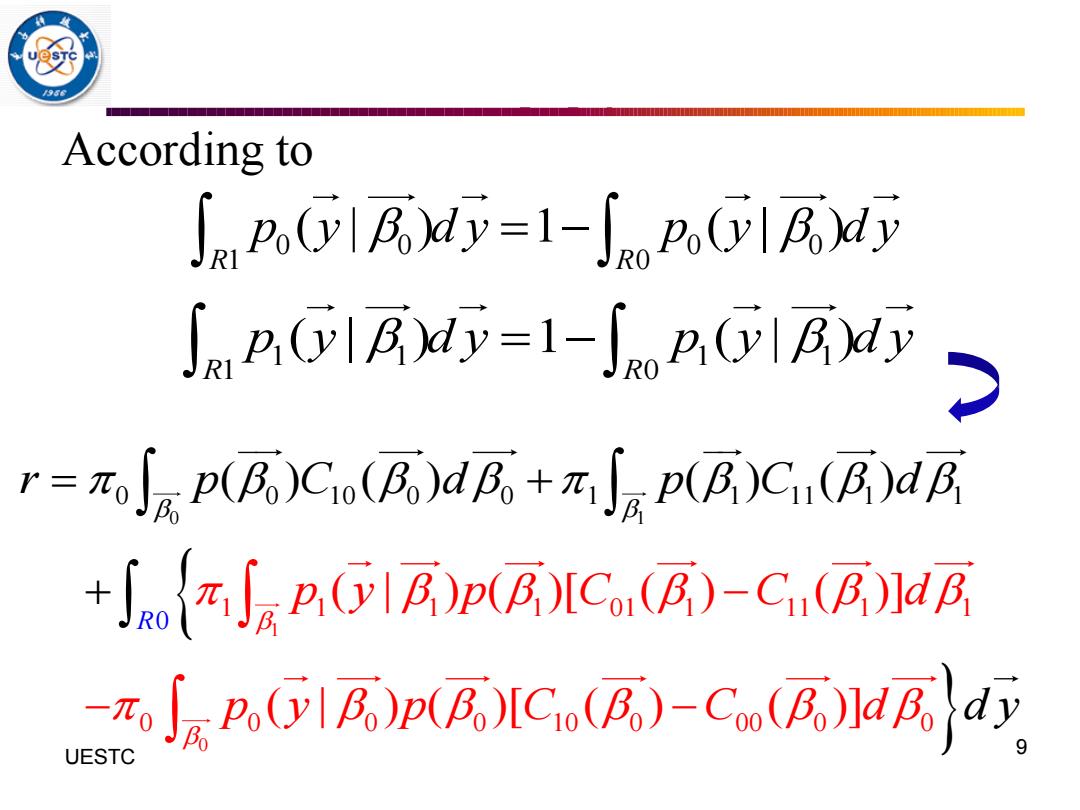
According to ∫npG1R=1-∫np,GRM pA1=1-∫Bd) ·=πjp(RC(R)HR+元p(B)C(B)dE (BIC(B)-Cu( -p,G1A)p(RIC(A)-C瓜p
9 UESTC According to 0 1 1 0 1 1 1 1 01 1 11 0 0 1 1 1 0 0 0 0 10 0 00 0 0 0 0 1 1 11 1 1 0 0 ( | ) ( )[ ( ) ( ) ( ) ( ) ( ] ( | ) ( )[ ( ) ( ) ) ] ) ( R p y p C C d r p C d p C d p y p C C d d y = − − + + − 0 0 0 0 1 0 ( | ) 1 ( | ) R R p y d y p y d y = − 1 1 1 1 1 0 ( | ) 1 ( | ) R R p y d y p y d y = −

r is minimized and Do is chosen when )p(B)ICu(B)-C(B)dB< 云P,A,pA[C(®)-C(AHR(6.12) Generally,the cost of making a mistake is greater than the cost of a correct decision.In other words, Co(B)>C(B) Cio(B)>Coo(Bo) UESTC 10
10 UESTC r is minimized and D0 is chosen when 1 0 1 1 1 1 01 1 11 1 1 0 0 0 0 10 0 00 0 0 ( | ) ( )[ ( ) ( )] ( | ) ( )[ ( ) ( )] (6.12) p y p C C d p y p C C d − − Generally, the cost of making a mistake is greater than the cost of a correct decision. In other words, 01 1 11 1 10 0 00 0 ( ) ( ) ( ) ( ) C C C C