
4.3.3.3气体的导热系数 气体的导热系数:0.006~0.67W/(mC) 温度的影响:t↑,入个 P的影响 冬一般压强范围内,入随压强变化很小,可忽略 过高(>2×105kPa)、过低(<3kPa)时,P↑,入↑气体的导 热系数小,对导热不利,但有利于保温。绝热、常压下气体 混合物的导热系数的估算式: 入m ∑2y,MV3 Ey,Ms 式中:y~组分的摩尔分率 M:-组分的分子量,kg/kmo
4.3.3.3 气体的导热系数 气体的导热系数:0.006~0.6 7W/(m·℃) 温度的影响:t↑,λ↑ P的影响 ❖一般压强范围内,λ随压强变化很小,可忽略 ❖过高(>2×105kPa)、过低(<3kPa)时,P ↑,λ↑ 气体的导 热系数小,对导热不利,但有利于保温。绝热、常压下气体 混合物的导热系数的估算式: 式中:yi-组分i的摩尔分率 Mi-组分i的分子量,kg/kmol 1/3 1/3 i i i i i m y M y M =
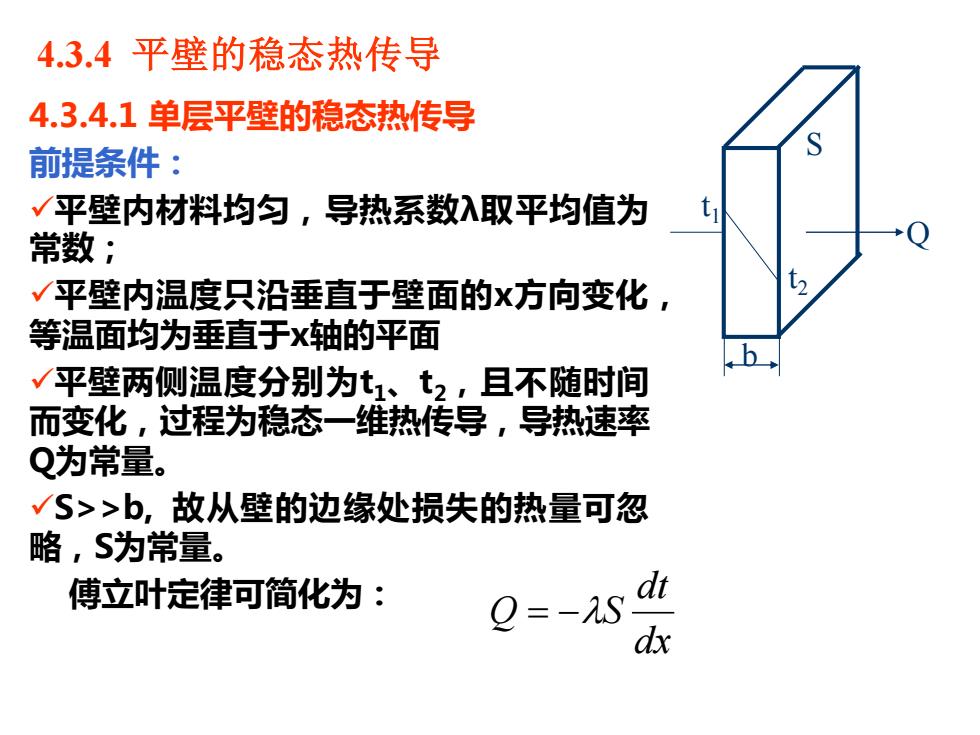
4.3.4平壁的稳态热传导 4.3.4.1单层平壁的稳态热传导 前提条件: √平壁内材料均匀,导热系数入取平均值为 t 常数; √平壁内温度只沿垂直于壁面的x方向变化, 等温面均为垂直于x轴的平面 √平壁两侧温度分别为t1、t2,且不随时间 而变化,过程为稳态一维热传导,导热速率 Q为常量。 √S>>b,故从壁的边缘处损失的热量可忽 略,S为常量。 傅立叶定律可简化为: dt O=-AS dx
4.3.4 平壁的稳态热传导 4.3.4.1 单层平壁的稳态热传导 前提条件: ✓平壁内材料均匀 ,导热系数 λ取平均值为 常数; ✓平壁内温度只沿垂直于壁面的 x方向变化 , 等温面均为垂直于 x轴的平面 ✓平壁两侧温度分别为 t 1 、 t 2 ,且不随时间 而变化 ,过程为稳态一维热传导 ,导热速率 Q为常量 。 ✓S>>b, 故从壁的边缘处损失的热量可忽 略,S为常量。 傅立叶定律可简化为: S Q b t 1 t 2 dx dt Q = − S

积分限:X=0一b,t=t1一t2积分 Qk=f广-Sd →0- 64-5)= △t R 热通量:9- 64-5)= S b R b 式中:R= 一 导热热阻,℃/W AS R'= b一 导热热阻,m2.℃/W 〖说明〗 √推动力为△t,阻力为RR) √导热速率与温度差、传热面积、导热系数成正比,而与平壁厚度成反 比。 V,R↑;Q=常数时,△t∝R √)=常数:=fx)为直线;入=入o(1+B):仁fx)为曲线 √热阻概念的应用: 冬计算界面温度或物体内温度分布 冬从温度分布判断各部分热阻的大小
积分限:x=0—b,t=t1—t2 积分 t x 0 b t1 t2 W W R t t t S b Q R t t t b S Qdx Sdt Q t t b m · / b R' / S b R ' ( ) ( ) 2 1 2 1 2 0 2 1 -导热热阻, ℃ 式中: -导热热阻,℃ 热通量: = = = − = = − = − = 〖说明〗 ✓推动力为Δt,阻力为R(R′) ✓导热速率与温度差、传热面积、导热系数成正比,而与平壁厚度成反 比。 ✓λ↓,R↑;Q=常数时,Δt∝R ✓λ =常数:t=f(x)为直线; λ = λ 0 (1+βt):t=f(x)为曲线 ✓热阻概念的应用: ❖计算界面温度或物体内温度分布 ❖从温度分布判断各部分热阻的大小
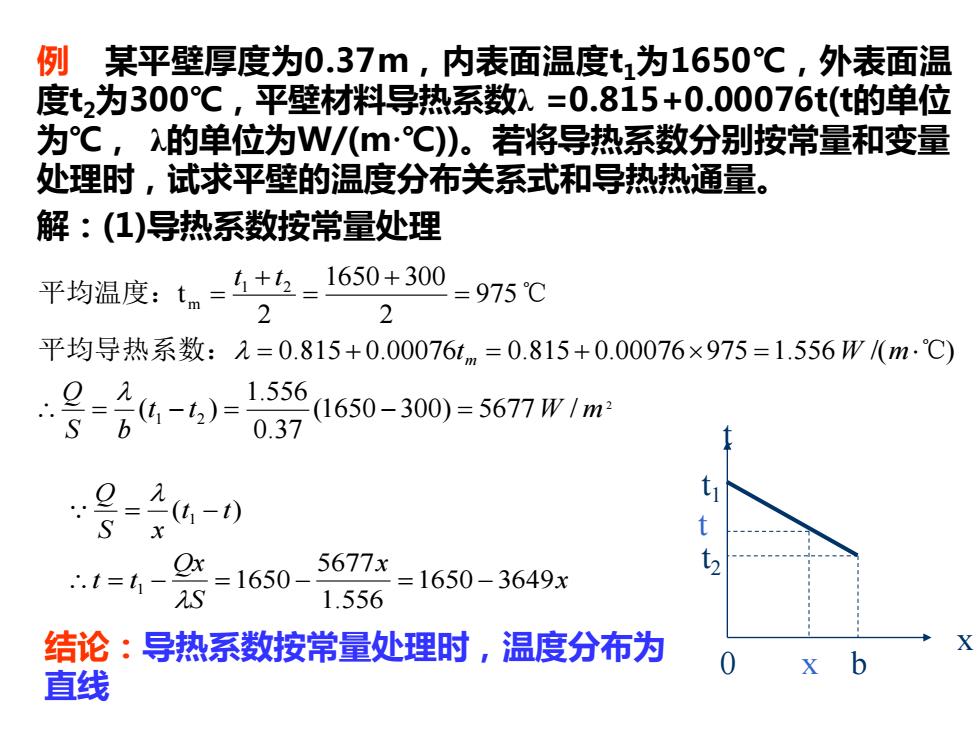
例某平壁厚度为0.37m,内表面温度t1为1650℃,外表面温 度t2为300℃,平壁材料导热系数=0.815+0.00076t(t的单位 为℃,2的单位为W/八m·C)。若将导热系数分别按常量和变量 处理时,试求平壁的温度分布关系式和导热热通量。 解:(1)导热系数按常量处理 平均温度:tn=+五-1650+300 975℃ 2 2 平均导热系数:2=0.815+0.00076tm=0.815+0.00076×975=1.556W(m.℃) 64-4)=1556 1650-300)=5677W/m2 0.37 t =(t1-t) S x Ox =1650- 5677x S 1.556 =1650-3649x 结论:导热系数按常量处理时,温度分布为 b 直线
例 某平壁厚度为0.37m,内表面温度t1为1650℃,外表面温 度t2为300℃,平壁材料导热系数λ =0.815+0.00076t(t的单位 为℃, λ的单位为W/(m·℃))。若将导热系数分别按常量和变量 处理时,试求平壁的温度分布关系式和导热热通量。 解:(1)导热系数按常量处理 2 (1650 300) 5677 / 0.37 1.556 ( ) 0.815 0.00076 0.815 0.00076 975 1.556 /( ) 975 2 1650 300 2 t 1 2 1 2 m t t W m S b Q t W m t t m = − = − = = + = + = = + = + = 平均导热系数: ℃ 平均温度: ℃ 结论:导热系数按常量处理时,温度分布为 直线 t x t t1 t2 b x 0 x x S Qx t t t t S x Q 1650 3649 1.556 5677 1650 ( ) 1 1 = − = − = − = −
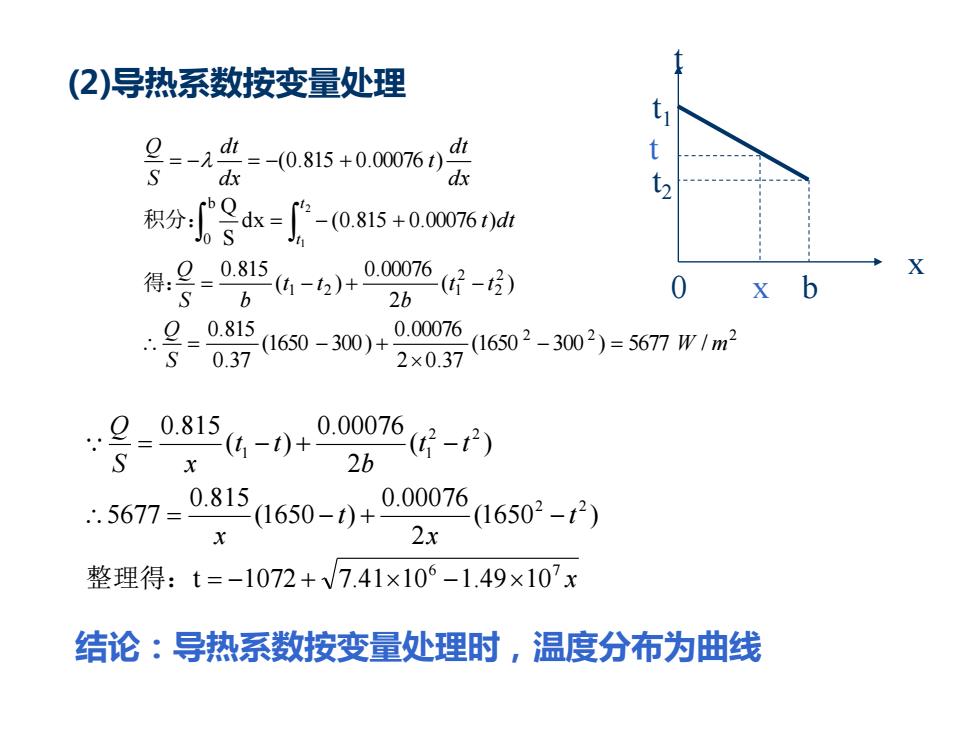
(2)导热系数按变量处理 g-元-0.815+0.00761 t dx dx 积分-085+0wn61 8=6(4-3)+0.00076 得,9-0815 t-) 2b x b :9=0.815 1650-300)+ 0.0007 2(16502-3002)=5677W1m2 S0.37 2×0.3 =0.815 S 6-0+00076g- 2b ·5677=0815 1650-0+D2¥16502-42) 整理得:t=-1072+√7.41×106-1.49×107x 结论:导热系数按变量处理时,温度分布为曲线
(2)导热系数按变量处理 2 2 2 2 2 2 1 2 1 b 0 (1650 300 ) 5677 / 2 0.37 0.00076 (1650 300) 0.37 0.815 ( ) 2 0.00076 ( ) 0.815 d x (0.815 0.00076 ) S Q (0.815 0.00076 ) 2 1 W m S Q t t b t t S b Q t d t d x d t t d x d t S Q t t − = = − + = − + − = − + = − = − + 得: 积分: x t x t x t t b t t S x Q 6 7 2 2 2 2 1 1 t 1072 7.41 10 1.49 10 (1650 ) 2 0.00076 (1650 ) 0.815 5677 ( ) 2 0.00076 ( ) 0.815 = − + − = − + − = − + − 整理得: 结论:导热系数按变量处理时,温度分布为曲线 t x t t1 t2 b x 0