《物理化学》课程教学课件（PPT讲稿）第三章 化学势

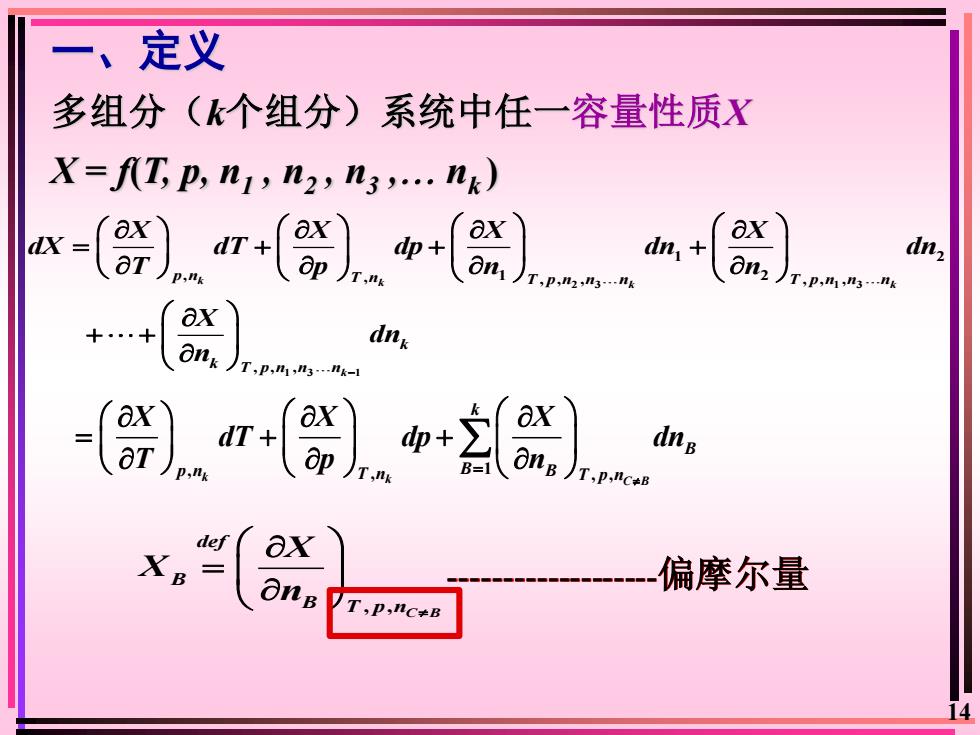
一、定义多组分（k个组分）系统中任一容量性质XX=f(T,p, ni, n2, n3.... nk)axaxax+(x)dT +dx =dn, +dnzapaTanP,nkT.nkT,P,n2,ng...nJT,p,ni,ng...nkaxdnk..+Onk/T,p,n,n3...nk-axaxax2dT+dp+dnaTBaponBB=p,nkTnJT,P,nc+BdefaxXB偏摩尔量=onBT,p,nc+B14

14 一、定义 多组分（k个组分）系统中任一容量性质X 2 3 1 3 1 3 1 1 2 , , 1 2 , , , , , , , , , k k k k k p n T n T p n n n T p n n n k k T p n n n X X X X dX dT dp dn dn T p n n X dn n −             = + + +                        + +     , , C B def B B T p n X X n     =      -偏摩尔量 X = f(T, p, n1 , n2 , n3 , nk ) , 1 k , , , k C B k B p n T n B B T p n X X X dT dp dn T p n  =          = + +                

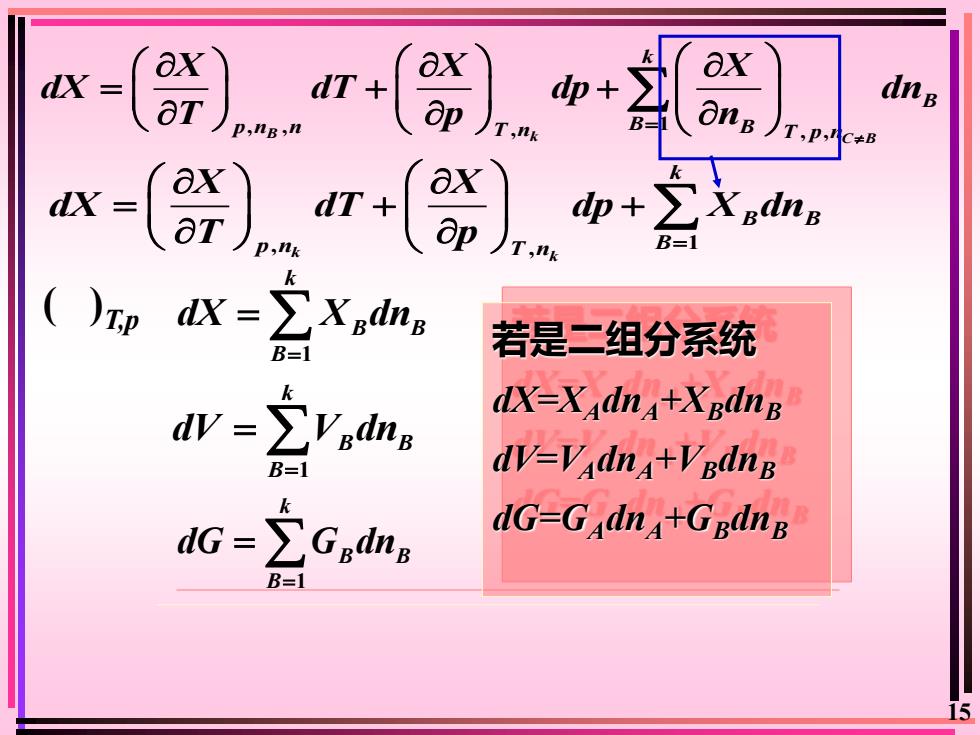
Kaxaxax1dX:dT+dp +dnB一aTOnBapB/T,p,c+BT,nkp,nB,nkaxaxEXednBdxdT +dp +aTopB=1JT,nkp,nkkZXpdnbdX =R若是二组分系统B=1kdX-X.dn+XBdnBdV=ZiVBdngdV-VAdnA+VBdnBB=1kdG-GAdnA+GBdnBEGadndG =B=115

15 , , 1 B , k , , C B k B p n n T n B B T p n X X X dX dT dp dn T p n  =          = + +                 1 k B B B dX X dn = =  1 k B B B dG G dn = =  ( )T,p , 1 k , k k B B p n T n B X X dX dT dp X dn T p =      = + +            1 k B B B dV V dn = =  若是二组分系统 dX=XAdnA+XBdnB dV=VAdnA+VBdnB dG=GAdnA+GBdnB

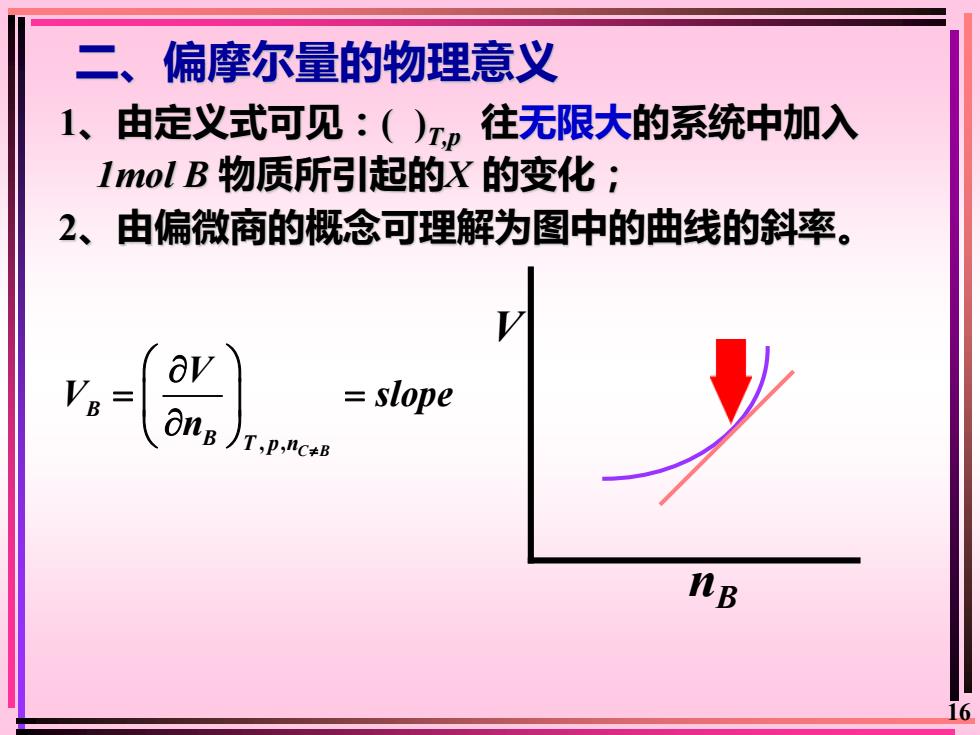
偏摩尔量的物理意义二、1、由定义式可见：（）T.p往无限大的系统中加入1molB物质所引起的X的变化；2、由偏微商的概念可理解为图中的曲线的斜率Vav= slopeonBJT,p,nc+BNB16

16 二、偏摩尔量的物理意义 1、由定义式可见：( )T,p 往无限大的系统中加入 1mol B 物质所引起的X 的变化； 2、由偏微商的概念可理解为图中的曲线的斜率。 , , C B B B T p n V V slope n     = =     V nB

三、集合公式一系统：A和B的偏摩尔体积分别为VA,VB 则 ()r,pdV=Vadn+Vdn如果由纯物质A(nA)，B(np)配置该系统：连续加入A和B，并保持系统组成不变，即dna：dnB=na：nB则dV =dn+Vpdn?

17 三、集合公式 则 B n A B n A V dV V dn V dn A B    = + 0 0 0 一系统：A和B的偏摩尔体积分别为 VA ,VB 则 ( )T,p dV=VAdnA+VBdnB 如果由纯物质A(nA), B(nB)配置该系统: 连续加入A 和B，并保持系统组成不变，即dnA : dnB = nA : nB

由于制备过程中保持浓度不变，故偏摩尔体积不变：nBdV=Vdnpdn +V-BJorV= VAna+ VenB集合公式X= Xana+ XpnBkZ若系统有个k组分：X =XBnBB-1kNG=,GBnBB=118

18 V = VAnA+ VBnB 若系统有个k组分： 1 k B B B X X n = =  1 k B B B G G n = =  B n A B n A V dV V dn V dn A B    = + 0 0 0 X = XAnA+ XBnB -集合公式 由于制备过程中保持浓度不变，故偏摩尔体积不变：