屈曲类型 结构失稳(屈曲) ,跃越屈曲(跳跃失稳) 必须考虑几何非线性,但不一定必须考虑弹塑性 挠度 特征:曲线既无分岔点也无极值点,结构以大幅度的变形从一个平 衡位形跳到另一个平衡位形。铰接坦拱,油罐的扁球壳顶盖
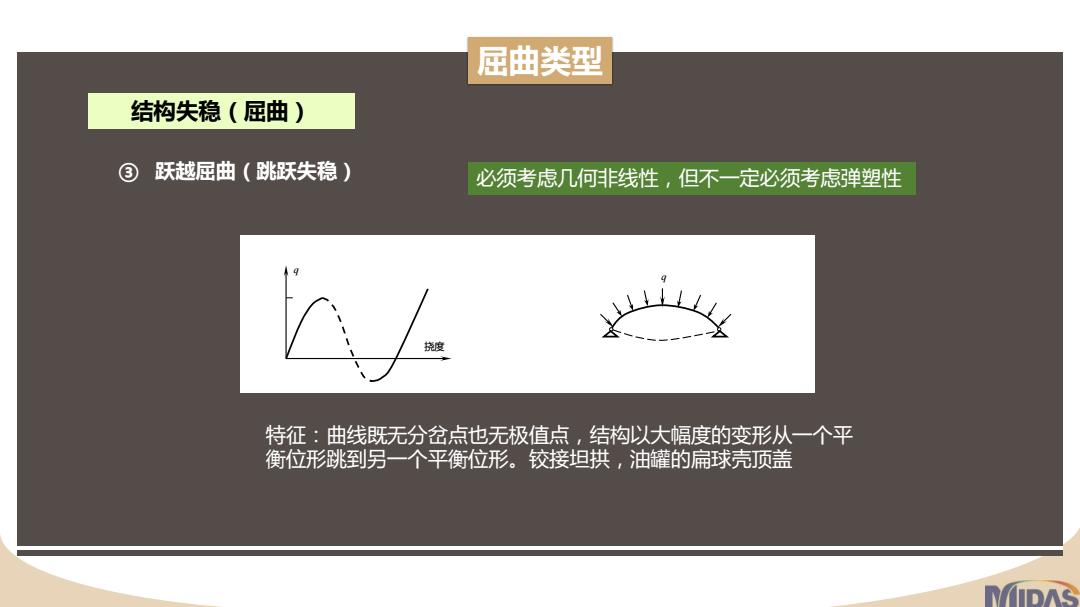
屈曲类型 结构失稳(屈曲) ③ 跃越屈曲(跳跃失稳) q 挠度 q 特征:曲线既无分岔点也无极值点,结构以大幅度的变形从一个平 衡位形跳到另一个平衡位形。铰接坦拱,油罐的扁球壳顶盖 必须考虑几何非线性,但不一定必须考虑弹塑性

计算方法 结构失稳(屈曲) 静力平衡法 (欧拉方法),求解系统平衡路径(曲线)分支点所对应 的载荷值(临界荷载) 缺陷法 求解具有初始缺陷的结构的变形过分大时的荷载值。 稳定问题的 计算方法 能量法 (铁木辛科法),基于拉格朗日定理。 振动法 以动力学观点来研究稳定问题。假定体系由于某种扰动绕 所讨论的平衡位置作微小自由振动,其振动频率与体系上 的荷载有关。当荷载增大时,频率会变小。当荷载趋近于 临界值(屈曲荷载)时,振动频率趋近于零
计算方法 结构失稳(屈曲) 稳定问题的 计算方法 静力平衡法 缺陷法 能量法 振动法 (欧拉方法),求解系统平衡路径(曲线)分支点所对应 的载荷值(临界荷载) 求解具有初始缺陷的结构的变形过分大时的荷载值。 (铁木辛科法),基于拉格朗日定理。 以动力学观点来研究稳定问题。假定体系由于某种扰动绕 所讨论的平衡位置作微小自由振动,其振动频率与体系上 的荷载有关。当荷载增大时,频率会变小。当荷载趋近于 临界值(屈曲荷载)时,振动频率趋近于零
计算方法 结构失稳(屈曲) 线性屈曲分析(即特征值屈曲分析) 完善体系 直杆(无初曲率) (用计算机分析) 理想体系) 中心受压(无初偏心) 结构稳定分析方法 非线性屈曲分析(几何非线性失稳分析) 具有初曲率的压杆 非完善体系 承受偏心荷载的压杆
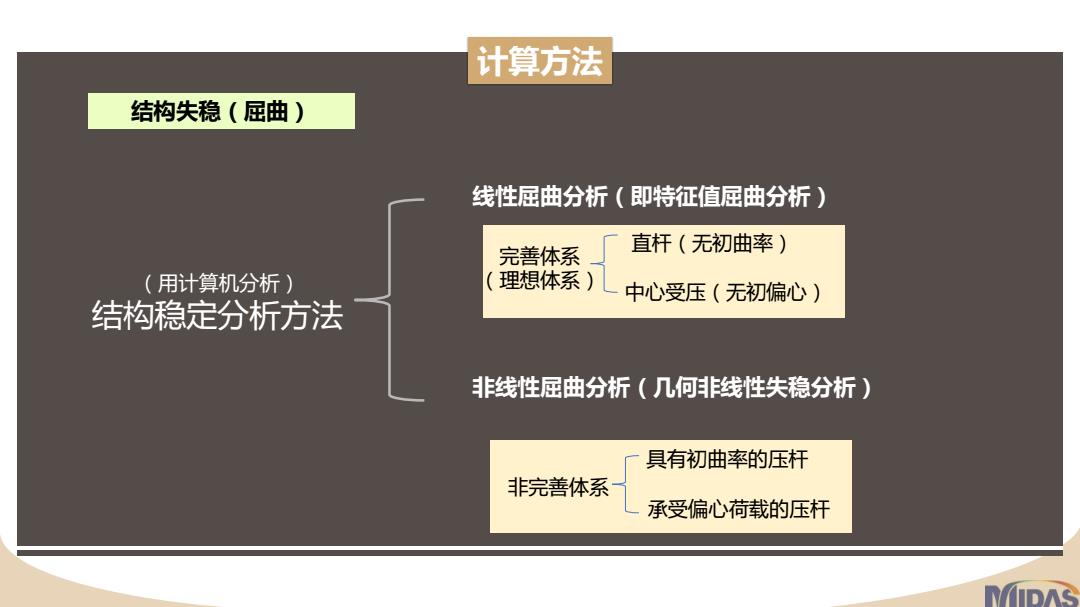
计算方法 结构失稳(屈曲) (用计算机分析) 结构稳定分析方法 线性屈曲分析(即特征值屈曲分析) 非线性屈曲分析(几何非线性失稳分析) 直杆(无初曲率) 中心受压(无初偏心) 完善体系 (理想体系) 非完善体系 具有初曲率的压杆 承受偏心荷载的压杆

结构稳定问题 基本理论 ·稳定性的基本概念 ·结构失稳类型及计算方法 ·线性屈曲分析与非线性屈曲分析
• 稳定性的基本概念 结构稳定问题 1 基本理论 • 结构失稳类型及计算方法 • 线性屈曲分析与非线性屈曲分析 • 稳定性的基本概念

线性屈曲分析 midas Gen的线性屈曲分析功能主要用于求解由桁架,梁单元或者板单元构成的结构 临界荷载系数和分析对应的屈曲模态。 在一定变形状态下的结构静力平衡方程式可以写成下列形式: 结构弹性刚度矩阵 [K]U+[KG]U=(P) 结构外力特征矢量 结构几何刚度矩阵 {U仍一结构位移特征矢量 (初应力刚度矩阵 数学角度-一当K+1Kc=0时,方程有特殊解,按照特征值问题 求解得到值及其对应的特征向量; [K +AKG]u=(P} 物理意义一一当刚度矩阵的行列式为0时,结构达到临界状态λ为临 界荷载,对应的特征值向量即为屈曲模态
线性屈曲分析 midas Gen 的线性屈曲分析功能主要用于求解由桁架、梁单元或者板单元构成的结构 临界荷载系数和分析对应的屈曲模态。 在一定变形状态下的结构静力平衡方程式可以写成下列形式: 结构弹性刚度矩阵 𝐾 𝑈 + 𝐾𝐺 𝑈 = 𝑃 𝑈 − 结构位移特征矢量 结构几何刚度矩阵 (初应力刚度矩阵) 结构外力特征矢量 𝐾 + 𝜆𝐾𝐺 u = 𝜆 𝑃 数学角度——当 𝐾 + 𝜆𝐾𝐺 = 0时,方程有特殊解,按照特征值问题 求解得到𝜆值及其对应的特征向量; 物理意义——当刚度矩阵的行列式为0时,结构达到临界状态𝜆为临 界荷载,对应的特征值向量即为屈曲模态