
山西移流字花 SHANXI INSTITUT在OF ENERO可 若有内热源, 少,山为P节点所在网格单元的内热源强度 测内热源发热量 Dp=Φwr·y1 在稳态导热下: DLn+PoP+①P+DP+DP=O 则 4w-24+山n-2,++9 4y2 入 第四章 导热问题的数值解法 16
第四章 导热问题的数值解法 16 若有内热源, 为P节点所在网格单元的内热源强度 则内热源发热量 在稳态导热下: 则 v,p =v,i, j x y 1 v,i, j 0 LP +QP +B P +TP +V P = 0 y t 2t t x t 2t t v,i, j 2 i, j 1 i, j i, j 1 2 i 1, j i, j i 1, j + = − + + + − + − + −
山西破源宇花 SHANXI INSTITUTE OF ENEROY 4.3边界节点离散方程的建立 及代数方程的求解 4.3.1边界节点离散方程的建立 1.位于平直边界上的节点 O ht=hty Ox P(i,》→t, y T T(i,j+1)→t, 21 l-Lj P Bi,j-1)→t- [i.l [(i-1,)→t-, tij-1 B 17
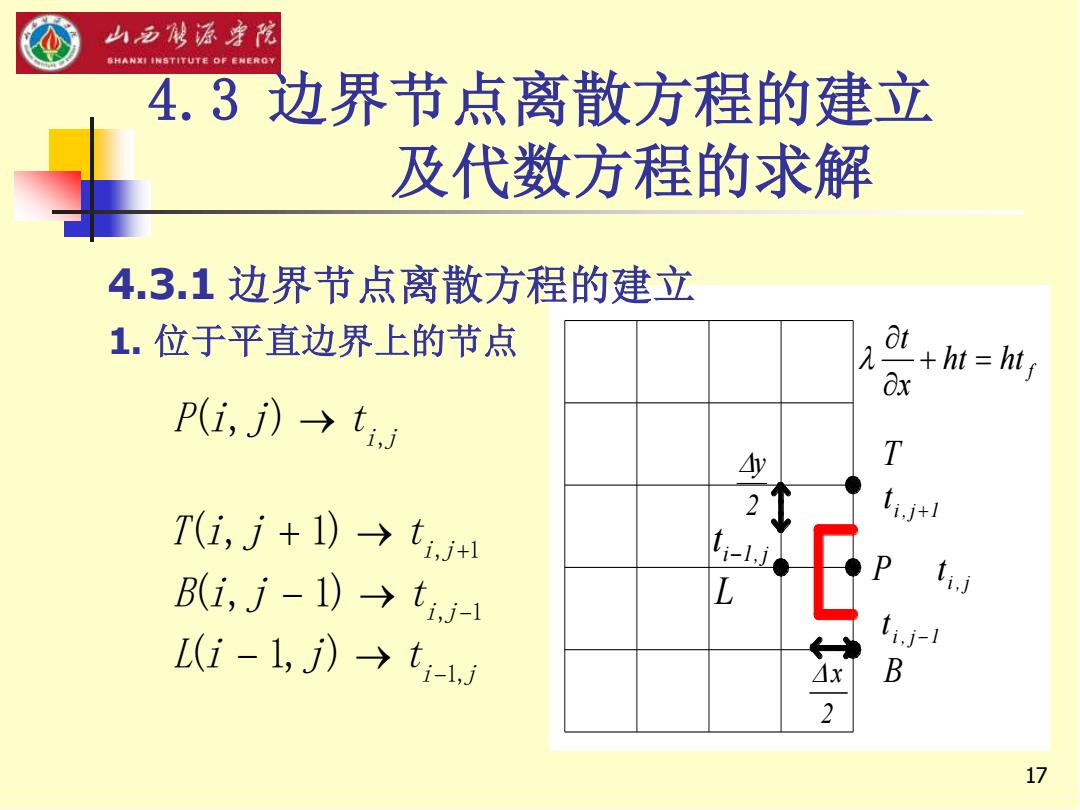
17 2 y i , j 1 t T + i , j P t B t i , j −1 L t i−1, j 2 x f ht ht x t + = 4.3 边界节点离散方程的建立 及代数方程的求解 4.3.1 边界节点离散方程的建立 1. 位于平直边界上的节点 , , 1 , 1 1, ( , ) ( , 1) ( , 1) ( 1, ) i j i j i j i j P i j t T i j t B i j t L i j t + − − → + → − → − →

山西成源宇院 SHANXI INSTITUTE OF ENEROY 红色框内为平直边界上P点的网格单元 边界条件:第三类边界 其热平衡式为: 山-y1+-u.1+-u. .1 △x △y 2 △y 2 +h,-t)△y-1=0 若为均匀网格,则上式可变形为: (4+2,=2x+7+im+2 18
18 红色框内为平直边界上P点的网格单元 边界条件:第三类边界 其热平衡式为: 若为均匀网格,则上式可变形为: ( ) 1 0 1 2 1 2 1 , 1, , , 1 , , 1 , + − = − + − + − − − + h t t y x y x t t y t t y x t t f i j i j i j i j i j i j i j i j i j i j i j f t h y t t t t h y = + + + 4 + 2 , 2 −1, , −1 , +1 2

山多能源宇花 SHANXI INSTITUTE OF ENEROY 注: 若有内热源,且内热源强度为①, 则可作上式左边加上内热源项少)少1中 ■绝热边界,只要令h=0,即可 ■第二类边界条件,即该平直边界面上有恒定热 流密度 第四章导热问题的数值解法 19
第四章 导热问题的数值解法 19 注: ◼ 若有内热源,且内热源强度为 则可在上式左边加上内热源项 ◼ 绝热边界,只要令h=0,即可 ◼ 第二类边界条件,即该平直边界面上有恒定热 流密度 1 v,i, j ) y 2 x ( v,i,j

山西限源宇院 SHANXI INSTITUTE OF ENEROY 设为qm则上式中的对流换热项,用热流密度qm来 替代 yAxAx.1 △x △y2 △y 2 +9w·△y1=0 20
20 设为qw 则上式中的对流换热项,用热流密度qw来 替代 1 0 1 2 1 2 1 1, , , 1 , , 1 , + = − + − + − − − + q y x y x t t y t t y x t t w i j i j i j i j i j i j