山西破源宇院 SHANXI INSTITUTE OF ENEROY 4.1导热问题数值求解的基本 思想及内节点 建立控制方程及定解条件 确定节点(区域离散化) 设立温度场的迭代初值 建立节点物理量的代数方程 离散方程的建立 求解代数方程 改进初场 是否收敛 是 解的分析 第四章 导热问题的数值解法 6
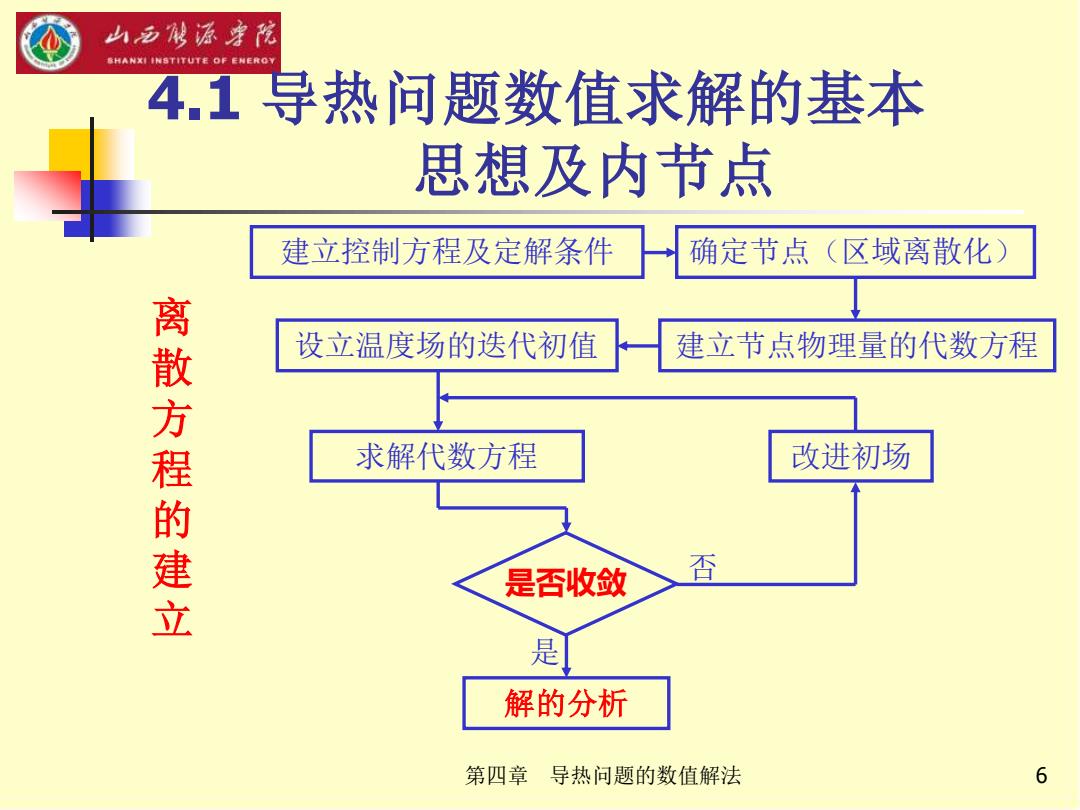
第四章 导热问题的数值解法 6 4.1 导热问题数值求解的基本 思想及内节点 离 散 方 程 的 建 立 建立控制方程及定解条件 确定节点(区域离散化) 设立温度场的迭代初值 建立节点物理量的代数方程 求解代数方程 是否收敛 解的分析 改进初场 是 否
山五限源宇花 SHANXI INSTITUTE OF ENEROY 区域温度场的离散化 N 导热问题的温度场是假设为 uE N 时间和空间的连续函数,当 进行数值求解时首先要做的 N 事情是在所研究的时间和空 K-1时刻 间区域内把时间和空间分割 S 成为有限大小的小区域。 K时刻 K+1时刻 X 原来连续变化的温度场就被一个离散的阶跃变化的温度 分布所代替。这就是连续变化的温度场离散化处理的基 本思路
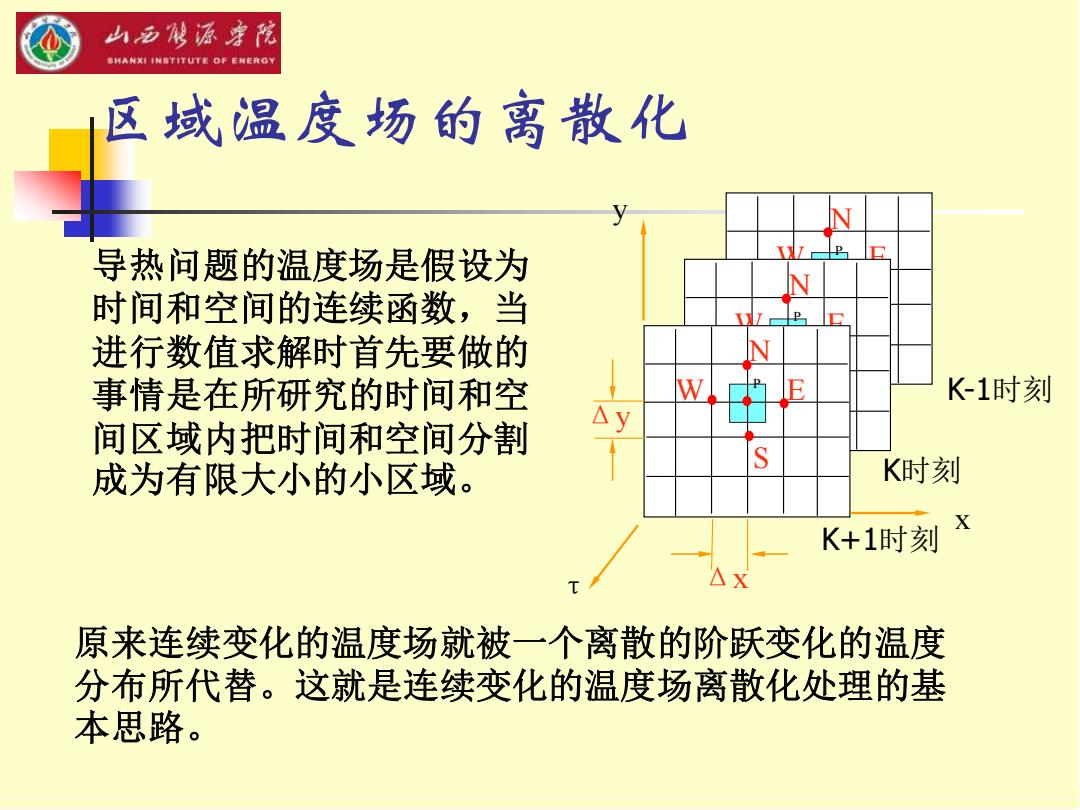
区域温度场的离散化 导热问题的温度场是假设为 时间和空间的连续函数,当 进行数值求解时首先要做的 事情是在所研究的时间和空 间区域内把时间和空间分割 成为有限大小的小区域。 K-1时刻 S W E N P S W E N P S W E N P τ x y K时刻 K+1时刻 Δx Δy 原来连续变化的温度场就被一个离散的阶跃变化的温度 分布所代替。这就是连续变化的温度场离散化处理的基 本思路
山多破源宇花 SHANXI INSTITUTE OF ENEROY ,j+1) (1+1)4y 网格单元 j4i+1,j2 (j-1)4y △x(i-1)》 iAx (i+1)△xx ■节点、→内节点 i,j广-1 边界节点 均匀网格c=y 内节点离散方程的建立
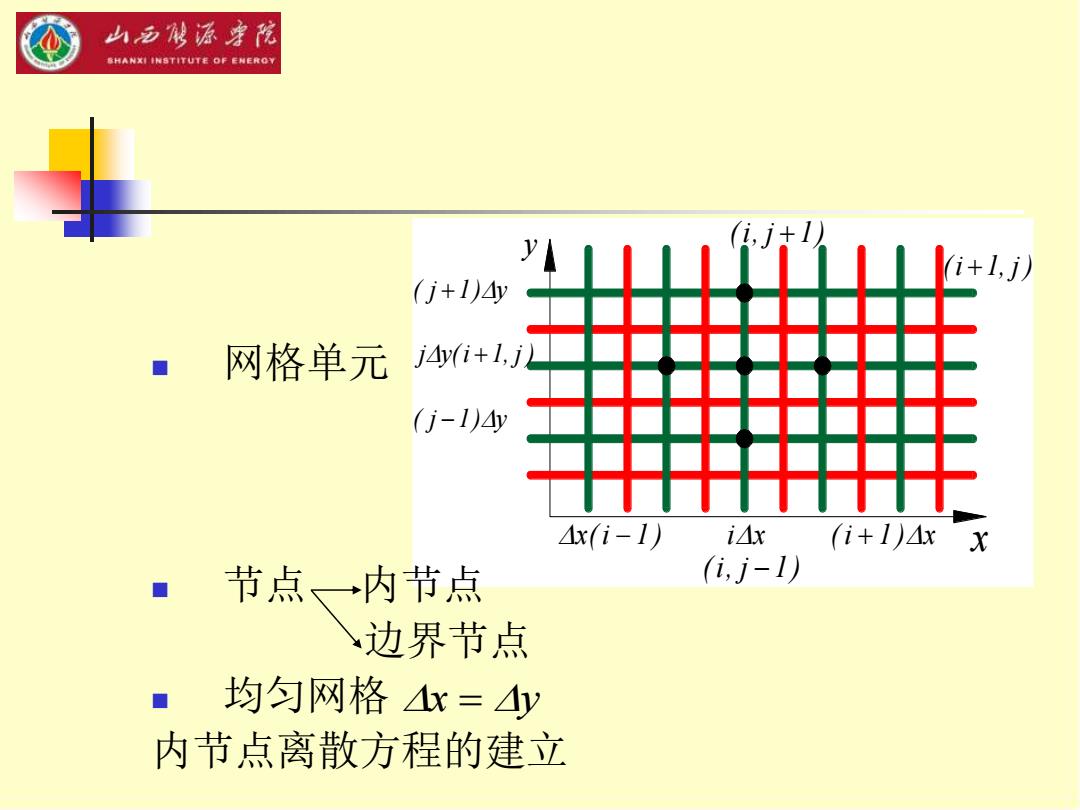
( j 1) y j y(i 1, j ) ( j 1) y − + + x( i − 1 ) ix ( i + 1 )x y x (i, j + 1) (i +1, j ) (i, j − 1) ◼ 网格单元 ◼ 节点 内节点 边界节点 ◼ 均匀网格 内节点离散方程的建立 x = y

山西限源宇院 SHANXI INSTITUTE OF ENEROY 4.2内节点离散方程的建立方法 用有限差分近似微分,用有限差商近似微商(导数) dt△r 例温肇分数芳 dx 蚀西将导热偏微分方程转化为节 建立节点离散方程的方法有两种: 泰勒级数展开法 热平衡法 第四章 导热问题的数值解法 9
第四章 导热问题的数值解法 9 4.2 内节点离散方程的建立方法 用有限差分近似微分,用有限差商近似微商(导数) dt t dx x 例如 :xdx, ,进而将导热偏微分方程转化为节 点温度差分代数方程。 建立节点离散方程的方法有两种: 泰勒级数展开法 热平衡法

山西成源宇院 SHANXI INSTITUTE OF ENEROY 1泰勒级数展开法 根据泰勒级数展开式,用节点(i,)的温度t红, 来表示节点(i+1,)而温度ti+1,j 4+w=t+( ,+, a3t、 Ar 3 用节点红,》的温度t五,来表示节点(i-1,)的 温度ti-1,j 、 十… 31 10
10 1 泰勒级数展开法 根据泰勒级数展开式,用节点(i,j)的温度ti,j 来表示节点(i+1,j)而温度ti+1,j 用节点(i,j)的温度ti,j来表示节点(i-1,j)的 温度ti-1,j + + + + = + 3! x ) x t ( 2! x ) x t ) x ( x t t t ( 3 3 i, j 2 3 2 i, j 2 i 1, j i, j i, j + − + − = − 3! x ) x t ( 2! x ) x t ) x ( x t t t ( 3 3 i, j 2 3 2 i, j 2 i 1, j i, j i, j