
3-6一双原子分子的势能函数为 E(=E()22(75 式中r为二原子间的距离,试证明: (1)。为分子势能极小时的原子间距: (2)分子势能的极小值为-E。 (3) 当Ep(r)=O时,原子间距为 (4) 画出势能曲线简图 目录结束
3-6 一双原子分子的势能函数为 式中 r 为二原子间的距离,试证明: (1)r0 为分子势能极小时的原子间距; (2)分子势能的极小值为-E。 (3)当EP (r) = 0时,原子间距为 (4)画出势能曲线简图 E ( ) 2 r 12 0 r0 (r) EP = ( ) r r 6 0 目录 结束

解:()E=E〔(,22(79 由分子势能极小值的条件 、 dEp(r)=0 dr 2)-,w929的 dr =12(“9-1245-9=0 -12942)+127959=0 得:(9)1(9)→r=8→r=。 目录结束
0 d (r ) EP d r = d (r ) EP d r = E ( ) 2 r 12 0 r0 ( ) r r 6 0 d d r = ( ) = r r 11 0 12 r r0 ( ) 12( ) r r 5 0 2 r r0 2 0 ( ) = r r 11 0 12 r r0 ( ) 12( ) r r 5 0 2 r r0 + 2 0 r r0 6 6 = r =r0 由分子势能极小值的条件 ( r ) = r 11 0 ( ) r r 5 得: 0 E ( ) 2 r 12 0 r0 (r) EP = ( ) r r 6 解: 0 (1) 目录 结束
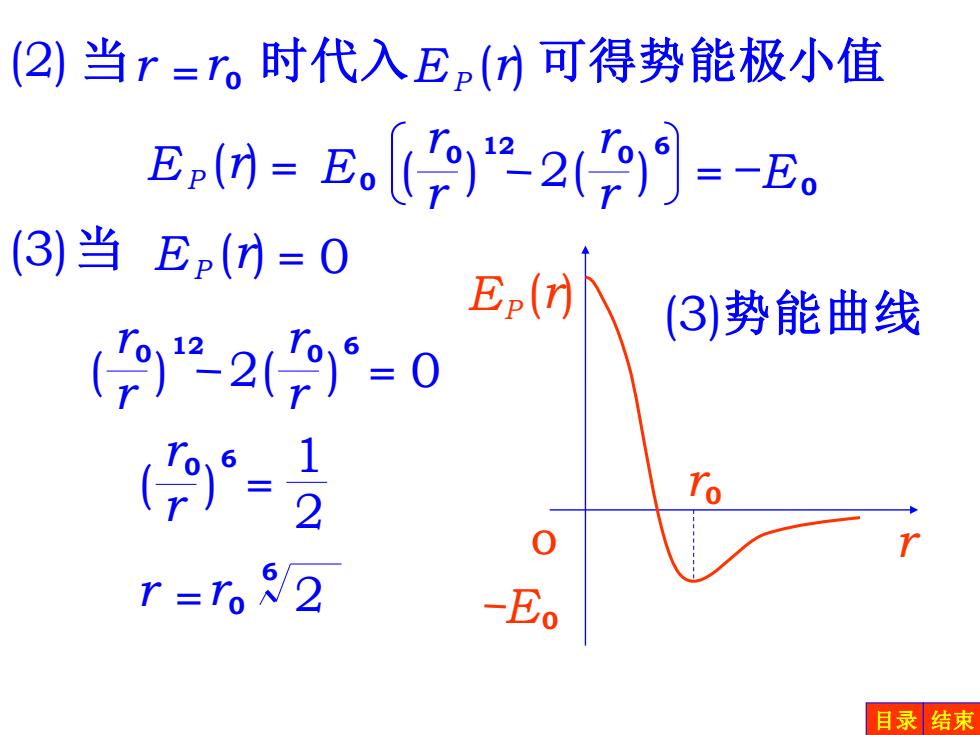
(2)当r=。时代入E()可得势能极小值 E()=E(922(99=-E。 3)当Ep()=0 E(r) (3)势能曲线 (2279)=0 9-2 r=。2 -E0 目录结束
E ( ) 2 r 12 0 r0 (r) EP = ( ) r r 6 0 = E0 ( ) 2 r r 12 0 ( ) r r 6 0 = 0 ( ) r r 6 0 = 2 1 r =r0 2 6 r =r0 (r) (2) 当 时代入EP 可得势能极小值 (r) (3)当 EP = 0 (r) EP r r0 o E0 (3)势能曲线 目录 结束
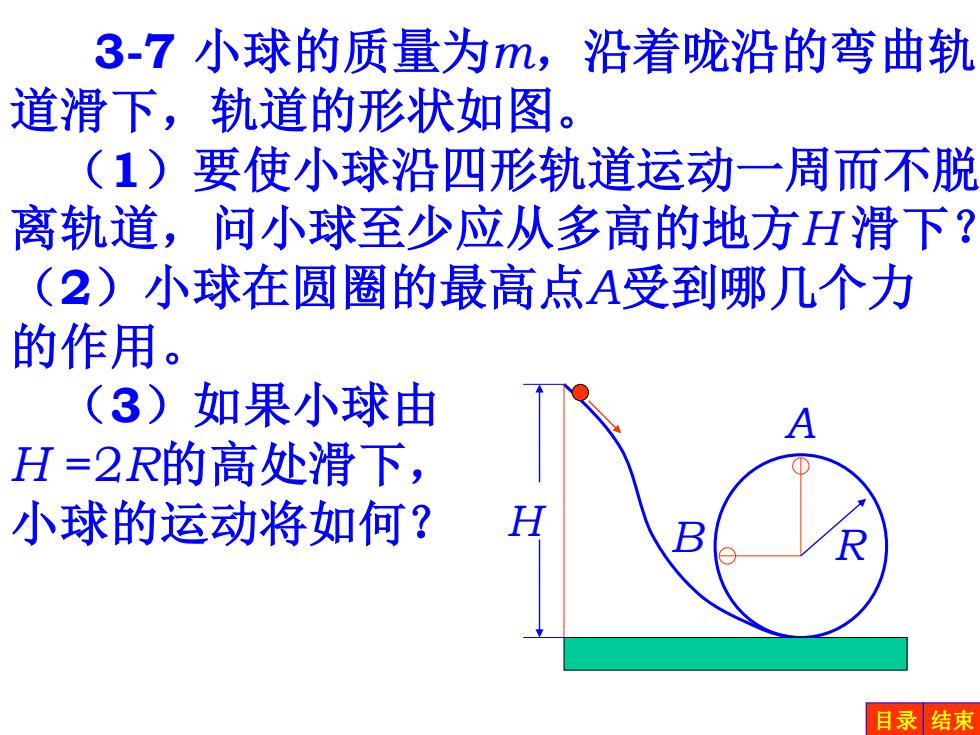
3-7小球的质量为m,沿着咙沿的弯曲轨 道滑下,轨道的形状如图。 (1)要使小球沿四形轨道运动一周而不脱 离轨道,问小球至少应从多高的地方H滑下? (2)小球在圆圈的最高点A受到哪几个力 的作用。 (3)如果小球由 H=2R的高处滑下, 小球的运动将如何? H 目录结束
3-7 小球的质量为m,沿着咙沿的弯曲轨 道滑下,轨道的形状如图。 (1)要使小球沿四形轨道运动一周而不脱 离轨道,问小球至少应从多高的地方H 滑下? (2)小球在圆圈的最高点A受到哪几个力 的作用。 (3)如果小球由 H =2R的高处滑下, 小球的运动将如何? A B R H 目录 结束
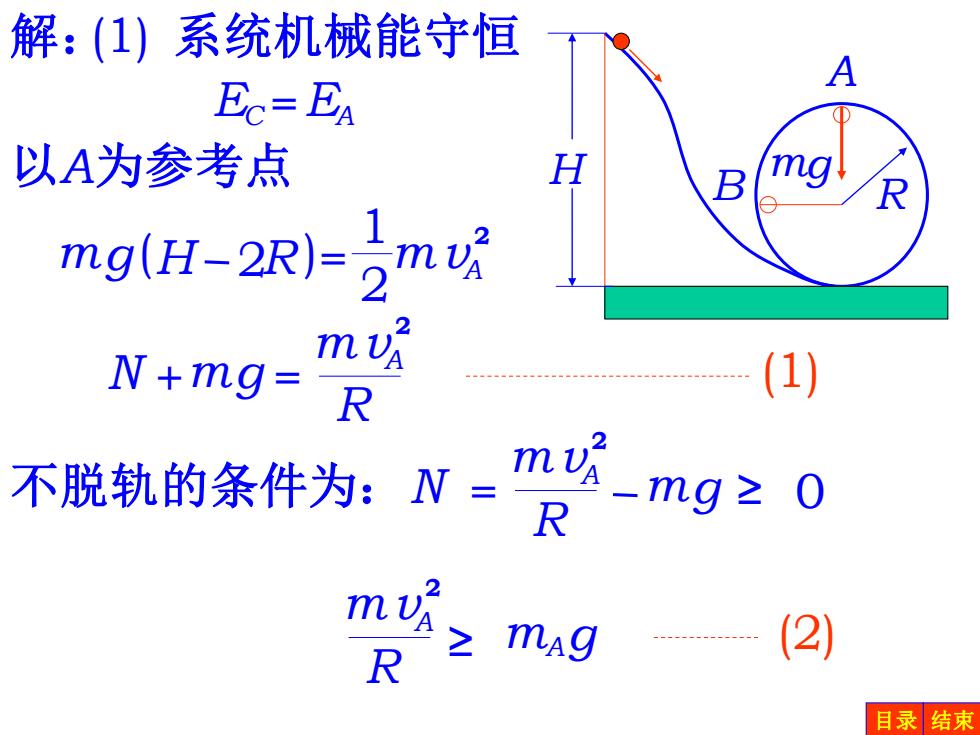
解:(1)系统机械能守恒 EC=EA 以A为参考点 mg(H-2R)-m N+mg= m Us R (1) 2 不脱轨的条件为:N= m-mg之0 R (2) 目录结束
A B R H mg 解:(1) 系统机械能守恒 EC =EA 以A为参考点 mg (H 2R ) mv 2 1 2 = A N = mg 0 mv 2 A R 不脱轨的条件为: ≥ N +mg = mv 2 A R (1) m g mv 2 A R ≥ A (2) 目录 结束