
C点: 经 N+F-mg=mR F=kxc=kR =mg 系统机械能守恒,选C点为零势能点。 2k+mg2R-1.6Rc0s0)=2m2+2x 解得:v=0.8gR an=R=0.8g an=0.8×9.8=7.84m/s2 02 N'-N-mR-0.8mg N 目录结束
C点: N+F = R c mg m v 2 ( ) 1 kxB 2 q 2 cos 2 +mg R 1.6R mv + 2 1 2 c 1 kxC 2 2 = an = v 2 c R = 0.8g an = 0.8×9.8=7.84m/s2 N ´ =N = m = v 2 c R 0.8mg N F =kxC = kR =mg 系统机械能守恒,选C点为零势能点。 v g 2 解得: c = 0.8 R 目录 结束

3-4一根特殊弹簧,在伸长xm时,沿它 伸长的反方向的作用力为(52.8x+38.4x2)N。 (1)试求把弹簧从=0.50拉长到x=1.00 时,外力克服弹簧力所作的功。 (2)将弹簧的一端固定,在另一端栓一质 量为2.17kg的物体,然后把弹簧拉到 x=1.00,开始无初速地释放物体,试求弹簧 缩回到=0.5。时物体的速率。 目录结束
3-4 一根特殊弹簧,在伸长x m时,沿它 伸长的反方向的作用力为(52.8x +38.4x2)N。 (1)试求把弹簧从x=0.50拉长到 x =1.00 时,外力克服弹簧力所作的功。 (2)将弹簧的一端固定,在另一端栓一质 量为 2.17 kg 的物体 ,然 后 把 弹 簧 拉到 x =1.00,开始无初速地释放物体,试求弹簧 缩回到x=0.5。时物体的速率。 目录 结束
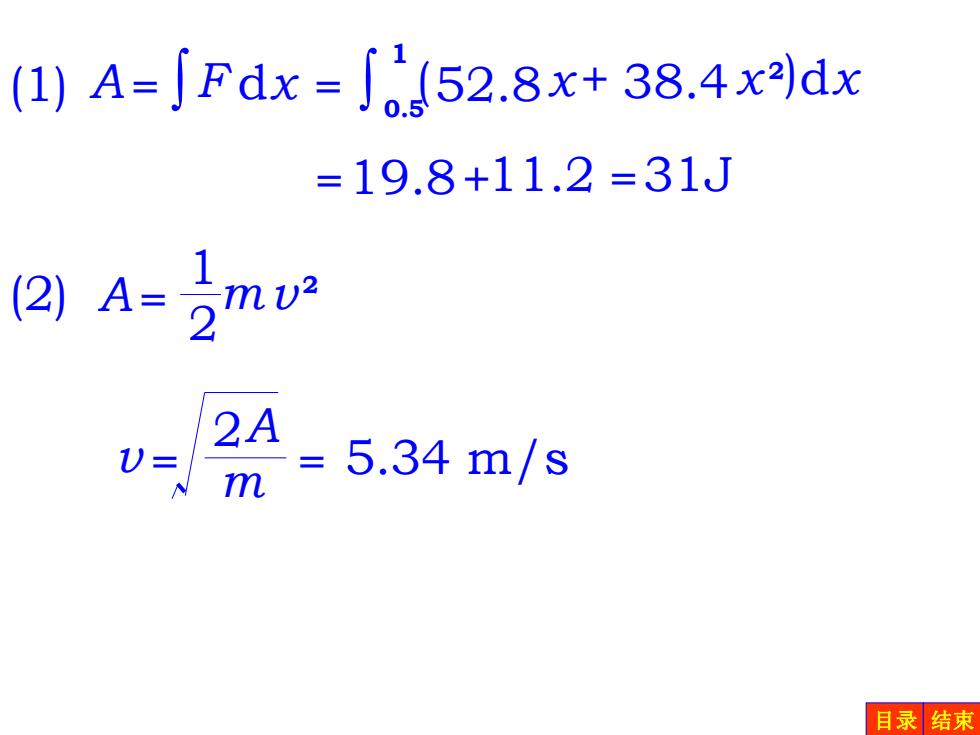
(1)A=JFdx=J52.8x+38.4x2)dx =19.8+11.2=31J (2)A= 2A m =5.34m/s 目录结束
=19.8+11.2 =31J 2 m v = A = 5.34 m/s A = ( x+ ) 2 0.5 x 1 (1) = F dx 52.8 38.4x d A= mv 2 1 2 (2) 目录 结束

3-5一质点沿x轴运动,势能为Ep(x, 总能量为E恒定不变,开始时静止于原点, 试证明当质点到达坐标x处所经历的时间 为: 目录结束
3-5 一质点沿 x 轴运动,势能为EP (x), 总能量为 E 恒定不变,开始时静止于原点, 试证明当质点到达坐标 x 处所经历的时间 为: 目录 结束
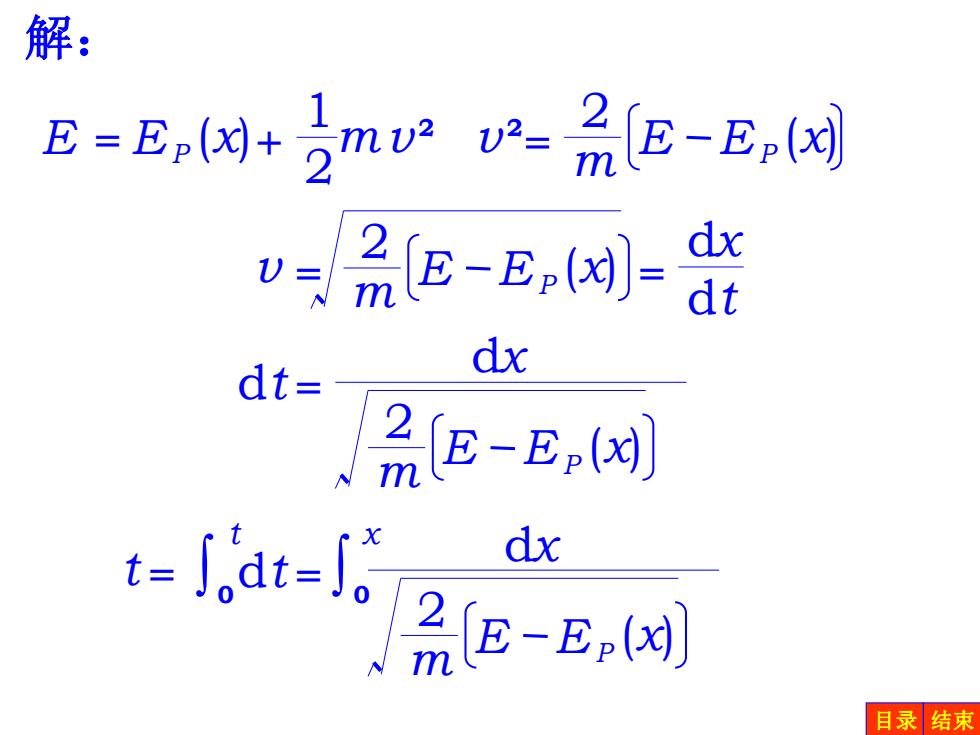
解: E=E(+2m2R-品E-E,(对 u=aE-E,(-= dx dx dt= -E t=Sodt-5o dx %E-E,(d) 目录结束
E (x) P mv 2 1 2 =E + 2 m v 2 = E (x) EP dt = 2 m v = E (x) EP dx dt = 2 m E (x) EP dx dt = 2 m E (x) EP dx t 0 t = x 0 解: 目录 结束