中南大学：《金属塑性加工原理》课程教学资源（PPT课件）第四篇 金属塑性变形力学解析方法 第7章 金属塑性加工变形力的工程法解析

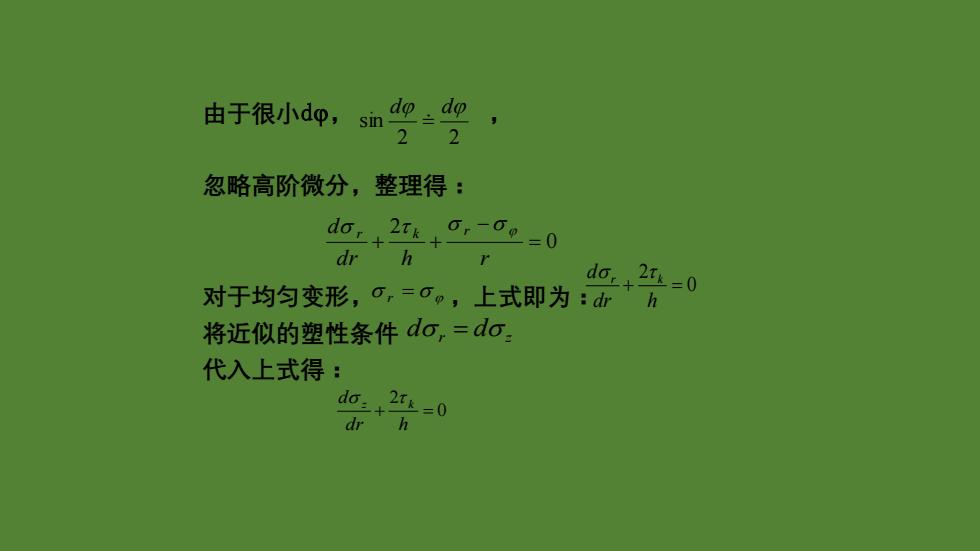
由于很小dp,sin 2 2 忽略高阶微分，整理得： do,2Tk 0,-0p=0 dr h 对于均匀变形，o,=o”,上式即为： 安头0 将近似的塑性条件do,=do. 代入上式得： do+2=0 dr h

由于很小d， ， 忽略高阶微分，整理得： 对于均匀变形， ，上式即为： 将近似的塑性条件 代入上式得： 2 2 sin d d = 0 2 = − + + d r h r d k r  r      r =   2 0 r k d dr h   + = d r = d z 0 2 + = dr h d z k  

接触面上正应力。 的分布规律 1.滑动区 Tk=fo. 2f0三=0 d h 上式积分得：。=C四(2) 当r=R时，o,=0,将近似塑性条件O:=o, 代入上式，得积分常数C1 C=o,exp 因此：a=a闻头R-

接触面上正应力 的分布规律 1．滑动区 上式积分得： 当r=R时， ，将近似塑性条件 代入上式，得积分常数C1 因此：  z k z  = f 0 2 =  + h f dr d z  z       = − h fr z C 2  1 exp  r = 0  z = s        = h f R C s 2 1  exp       = ( − ) 2 exp R r h f  z  s