
第2章金属塑性变形的物性方程 §2.1金属塑性变形过程和力学特点 §2.2塑性条件方程 §2.3塑性应力应变关系(本构关系) §2.4变形抗力曲线与加工硬化 §2.5影响变形抗力的因素
第2章 金属塑性变形的物性方程 §2.1 金属塑性变形过程和力学特点 §2.2 塑性条件方程 §2.3 塑性应力应变关系(本构关系) §2.4 变形抗力曲线与加工硬化 §2.5 影响变形抗力的因素
§2.1金属塑性变形过程和力学特点 变形过程与特点 以单向拉伸为例说明塑性变形过程与特点,如图2-1所示。金属变形 分为弹性、均匀塑性变形、破裂三个阶段。 o<o,时,G=E8 。 当o≥0,以后,变形视作塑性阶段。σ一6是 非线性关系。当应力达到。之后,变形转为不均匀 塑性变形,呈不稳定状态。经短暂的不稳定变形 试样以断裂告终。 若在均匀塑性变形阶段出现卸载现象,一部分 变形得以恢复,另一部分则成为永久变形。卸载阶 段σ一8呈线性关系。这说明了塑性变形时,弹性 图2-1单向拉伸的塑性变形特点 变形依然存在。弹塑性共存与加载卸载过程不同的 G-8 关系是塑性变形的两个基本特征
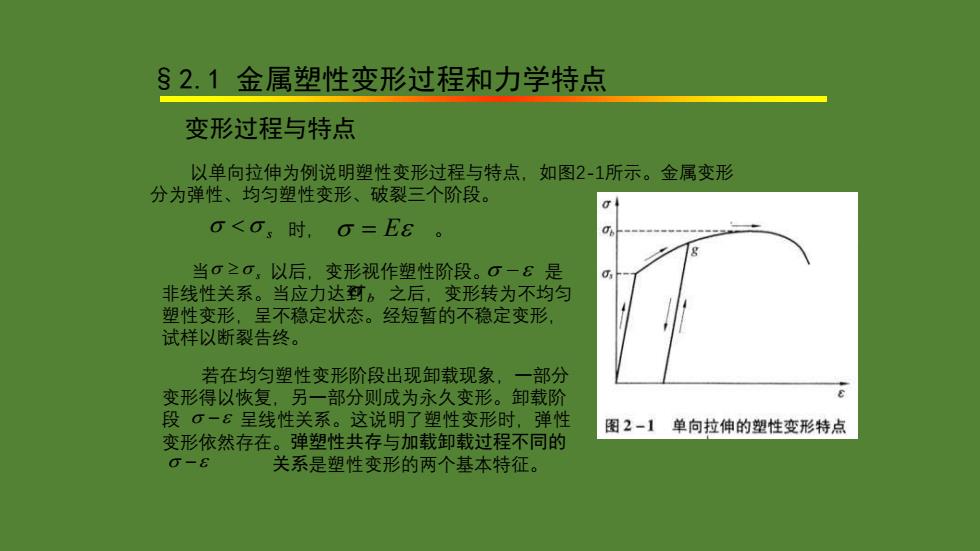
§2.1 金属塑性变形过程和力学特点 − 变形过程与特点 以单向拉伸为例说明塑性变形过程与特点,如图2-1所示。金属变形 分为弹性、均匀塑性变形、破裂三个阶段。 s 时, = E 。 当 以后,变形视作塑性阶段。 是 非线性关系。当应力达到 之后,变形转为不均匀 塑性变形,呈不稳定状态。经短暂的不稳定变形, 试样以断裂告终。 s − b 若在均匀塑性变形阶段出现卸载现象,一部分 变形得以恢复,另一部分则成为永久变形。卸载阶 段 呈线性关系。这说明了塑性变形时,弹性 变形依然存在。弹塑性共存与加载卸载过程不同的 − 关系是塑性变形的两个基本特征。 −

由于加载、卸载规律不同,导致·一£关系不唯一。只有知道变形 历史,才能得到一一对应的σ一关系,即塑性变形与变形历史或路径 有关。这是第3个重要特征。 事实上,σ>o以后的点都可以看成是重新加载时的屈服点。以g点 为例,若卸载则σ一£关系为弹性。卸载后再加载,只要σ<σ:点, σ-6关系仍为弹性。一旦超过g点,σ-8呈非线性关系,即g点也是 弹塑性变形的交界点,视作继续屈服点。一般有>·,这一现象为 硬化或强化,是塑性变形的第4个显著特点。 在简单压缩下,忽略摩擦影响,得到的压缩σ:与拉伸σ基本相 同。但是若将拉伸屈服后的试样经卸载并反向加载至屈服,反向屈服 一般低于初始屈服。同理,先压后拉也有类似现象。这种正向变形强 化导致后继反向变形软化的现象称作Bauschinger效应。这是金属微观 组织变化所致。一般塑性理论分析不考虑Bauschingers效应。 Bridgman等人在不同的静水压力容器中做单向拉伸试验。结果表 明:静水压力只引起物体的体积弹性变形,在静水压力不很大的情况 下(与屈服极限同数量级)所得拉伸曲线与简单拉伸几乎一致,说明 静水压力对塑性变形的影响可以忽略
由于加载、卸载规律不同,导致 关系不唯一。只有知道变形 历史,才能得到一一对应的 关系,即塑性变形与变形历史或路径 有关。这是第3个重要特征。 事实上, 以后的点都可以看成是重新加载时的屈服点。以g点 为例,若卸载则 关系为弹性。卸载后再加载,只要 点, 关系仍为弹性。一旦超过g点, 呈非线性关系,即g点也是 弹塑性变形的交界点,视作继续屈服点。一般有 ,这一现象为 硬化或强化,是塑性变形的第4个显著特点。 − − s − − − g g s 在简单压缩下,忽略摩擦影响,得到的压缩 与拉伸 基本相 同。但是若将拉伸屈服后的试样经卸载并反向加载至屈服,反向屈服 一般低于初始屈服。同理,先压后拉也有类似现象。这种正向变形强 化导致后继反向变形软化的现象称作Bauschinger效应。这是金属微观 组织变化所致。一般塑性理论分析不考虑Bauschinger效应。 Bridgman等人在不同的静水压力容器中做单向拉伸试验。结果表 明:静水压力只引起物体的体积弹性变形,在静水压力不很大的情况 下(与屈服极限同数量级)所得拉伸曲线与简单拉伸几乎一致,说明 静水压力对塑性变形的影响可以忽略。 s s

基本假设 材料为均匀连续,且各向同性; 一体积变化为弹性的,塑性变形时体积不变; ,静水压力不影响塑性变形,只引起体积弹性变化; 一不考虑时间因素,认为变形为准静态; 不考虑Bauschinger?效应
基 本 假 设 ➢材料为均匀连续,且各向同性; ➢体积变化为弹性的,塑性变形时体积不变; ➢静水压力不影响塑性变形,只引起体积弹性变化; ➢不考虑时间因素,认为变形为准静态; ➢不考虑Bauschinger效应

s2.2塑性条件方程 屈服准则又称塑性条件(Plastic conditions)或屈服 条件(Yield conditions),它是描述不同应力状态下变形体 某点进入塑性状态并使塑性变形继续进行所必须满足的力学 条件。 用屈服函数(Yield function)表示: f(o)=0 (ij=x,y,2) f(o,)=0 (i=12,3) f(I1,I2,I3)=0 fI5,I)=0
§2.2 塑性条件方程 屈服准则又称塑性条件(Plastic conditions)或屈服 条件(Yield conditions),它是描述不同应力状态下变形体 某点进入塑性状态并使塑性变形继续进行所必须满足的力学 条件。 用屈服函数(Yield function)表示: ( ) 0 ( , , , ) ij f i j x y z = = ( ) 0 ( 1,2,3) i f i = = 1 2 3 f I I I ( , , ) 0 = 2 3 f I I ( , ) 0 =