§7.2直角坐标平面应变问题解析 ,例题一 1.滑动摩擦条件下的矩形块平锤压缩变形(直角坐标平面应变问题) 高为h,宽为W,长为1 的矩形块,置于平锤下压 缩。如果1比W大得多, 则1方向几乎没有延伸, 0 仅在x方向和y方向有塑 性流动,即为平面应变 问题,适用于直角坐标 分析。 矩形工件的平锤压缩
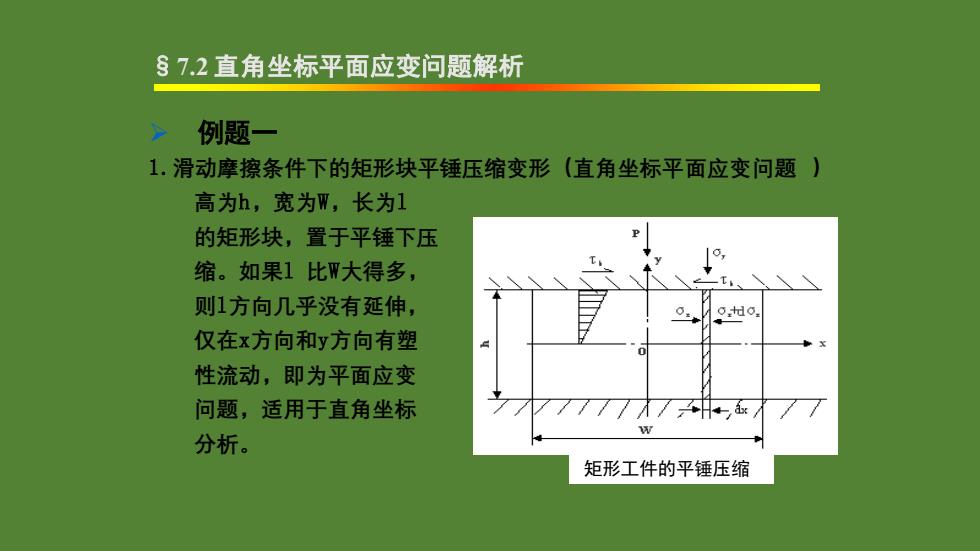
➢ 例题一 1.滑动摩擦条件下的矩形块平锤压缩变形(直角坐标平面应变问题 ) 高为h,宽为W,长为l 的矩形块,置于平锤下压 缩。如果l 比W大得多, 则l方向几乎没有延伸, 仅在x方向和y方向有塑 性流动,即为平面应变 问题,适用于直角坐标 分析。 矩形工件的平锤压缩 §7.2 直角坐标平面应变问题解析

(以图示应力方向推证。) 单元体x方向的力平衡方程为: o,h-(o,+do,)h-2tdx=0 整理后得:dox+2=0 dx h 由近似塑性条件 oy-ox=Kf 或-少=0得: h 将滑动摩擦时的库仑摩擦定律 Tk=foy 代入上式得: a,=_2fa, h 上式积分得:,=6四
(以图示应力方向推证。) 单元体x方向的力平衡方程为: 整理后得: 由近似塑性条件 或 ,得: 将滑动摩擦时的库仑摩擦定律 代入上式得: 上式积分得: x h −( x + d x )h − 2 k dx = 0 0 2 + = dx h d x k dx− dy = 0 dx h d y k 2 = − k y = f h f dx d y y 2 = − = x h f y C 2 1 exp σy-σx=Kf

在接触边缘处,即x=W/2 时,0x=0, 由近似塑性条件得口,=k 于是c=k,( 因此接触面上正应力分布规律 ,=K exp 20w-] h 最后求得板坯单位长度(亿向单位长度)上的变形 力P可求得为: P-a,=km月
在接触边缘处,即 时, , 由近似塑性条件得 于是 因此接触面上正应力分布规律 最后求得板坯单位长度(Z向单位长度)上的变形 力P可求得为: x =W / 2 x = 0 y f = k = h fW C K f exp − = h f W x y K f 2 (0.5 ) exp − = = 2 ( ) exp 1 / 2 0 h f W f h P dx Kf W y

§7.3圆柱坐标轴对称问题 下面讨论混合摩擦条件下,平锤均匀镦粗圆柱体时变 形力计算。圆柱体徽粗时,如果锻件的性能和接触表面状 态没有方向性,则内部的应力应变状态对称于圆柱体轴线 (z轴),即在同一水平截面上,各点的应力应变状态与φ 坐标无关,仅与坐标有关。因此是一个典型的圆柱体坐标 轴对称问题
下面讨论混合摩擦条件下,平锤均匀镦粗圆柱体时变 形力计算。圆柱体镦粗时,如果锻件的性能和接触表面状 态没有方向性,则内部的应力应变状态对称于圆柱体轴线 (z轴),即在同一水平截面上,各点的应力应变状态与 坐标无关,仅与r坐标有关。因此是一个典型的圆柱体坐标 轴对称问题。 §7.3 圆柱坐标轴对称问题
圆柱坐标轴对称问题 工件的受力情况如 .+d0。 右图所示。仍以图示受 力方向推证。分析它的 D 一个分离单元体的静 -0,4da. 力平衡条件,得: ah-o-a,+d,M+o-2,tt+2加,:dsn号=0
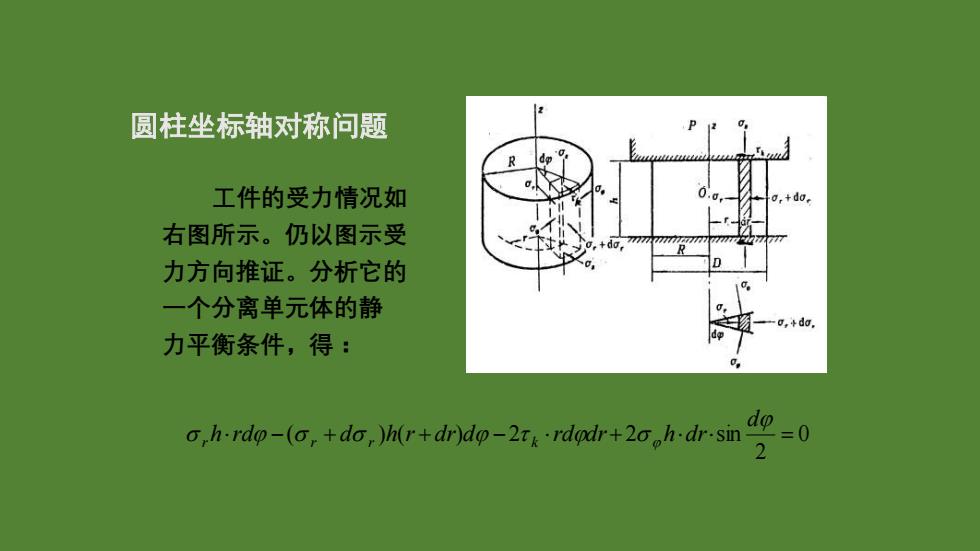
圆柱坐标轴对称问题 工件的受力情况如 右图所示。仍以图示受 力方向推证。分析它的 一个分离单元体的静 力平衡条件,得: 0 2 −( + ) ( + ) − 2 + 2 sin = d h rd d h r d r d rd d r h d r r r r k