
分析力学5动力学变分原理(5) 0x(t2)=0 Perturbed path t2 ‘6x True path 6x(t1)三0 zi(t) 西安电子科技大学 郭空明 q9:717004648 Email:kmguo@xidian.edu.cn
分析力学 5 动力学变分原理(5) 西安电子科技大学 郭空明 qq:717004648 Email:kmguo@xidian.edu.cn

4.1泛函与变分原理(1) 4.2哈密顿原理(2) 4.3连续系统的微振动(1) 4.4欧拉-拉格朗日方程(1)
4.1 泛函与变分原理(1) 4.2 哈密顿原理(2) 4.3 连续系统的微振动 (1) 4.4 欧拉-拉格朗日方程 (1)

力学的变分原理:提供一种准则,将真实的运动 (满足动力学方程)从所有可能的运动中甄别出 来。 具有更高的概括性和普适性
力学的变分原理:提供一种准则,将真实的运动 (满足动力学方程)从所有可能的运动中甄别出 来。 具有更高的概括性和普适性
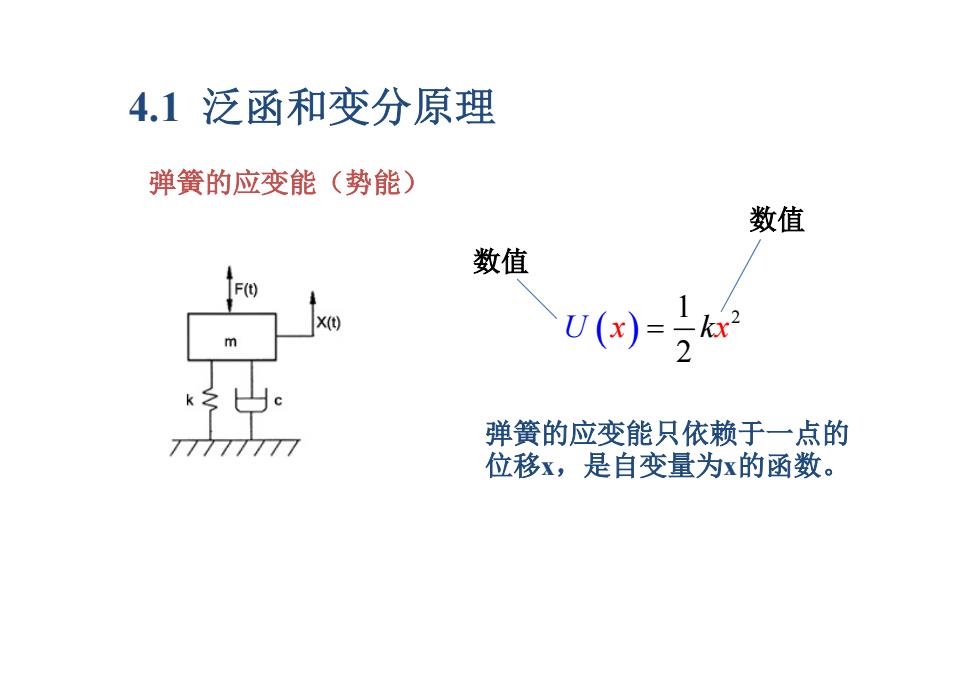
4.1泛函和变分原理 弹簧的应变能(势能) 数值 数值 F(t) U(x) 77777777 弹簧的应变能只依赖于一点的 位移x,是自变量为x的函数
4.1 泛函和变分原理 弹簧的应变能(势能) 1 2 2 U x kx 数值 数值 2 弹簧的应变能只依赖于一点的 位移x,是自变量为x的函数
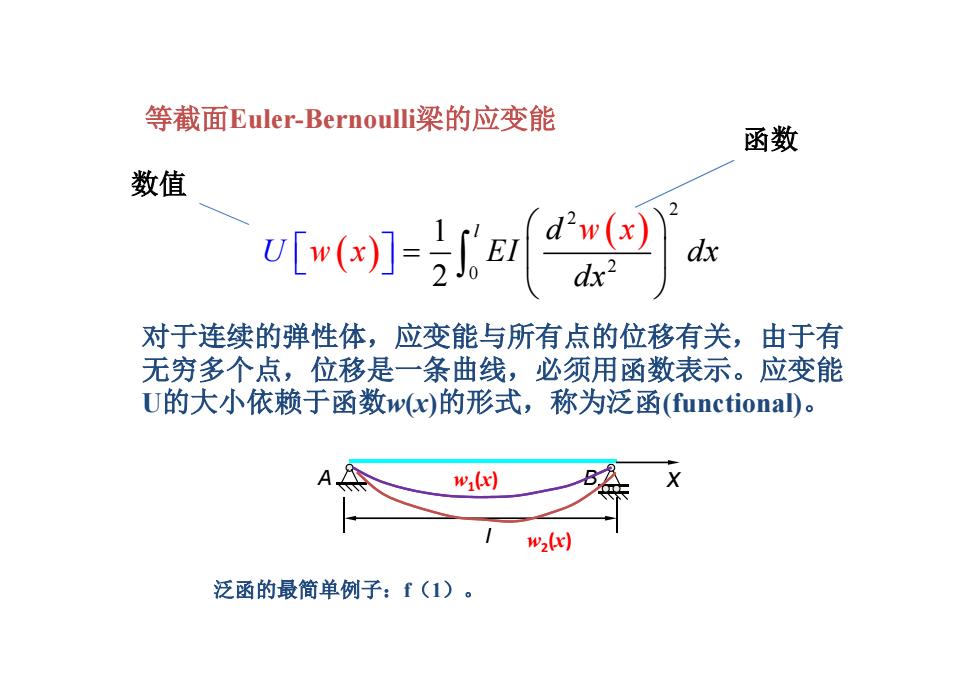
等截面Euler-Bernoulli梁的应变能 函数 数值 e1-〔oj dx 对于连续的弹性体,应变能与所有点的位移有关,由于有 无穷多个点,位移是一条曲线,必须用函数表示。应变能 U的大小依赖于函数w(c)的形式,称为泛函(functiona)。 A w(x) w(x) 泛函的最简单例子:f(1)
2 2 2 0 1 2 l d w x EI dx d U w x x 等截面Euler-Bernoulli梁的应变能 函数 数值 对于连续的弹性体,应变能与所有点的位移有关,由于有 无穷多个点,位移是一条曲线,必须用函数表示。应变能 U的大小依赖于函数w(x)的形式,称为泛函(functional)。 A B l x w2(x) w1(x) 泛函的最简单例子:f(1)