
函数的微分Differential of a function y=f(x) 当自变量X有一增量:△x=X1·X0 函数y也有一增量: △y 0 =y1-yo f(x)f(xo) dy △y=f(x)△x dx dy f(x)dx dy与dx,分别称为自变量X与 x+dx 函数y的微分。 一一 微分问题
y = f(x) 当自变量 x 有一增量: 函数 y 也有一增量: Δ 1 0 y = y - y 1 0 = f(x ) - f(x ) 1 0 Δx = x - x 函数的微分 Differential of a function 1 0 = f(x ) - f(x ) Δy = f (x) Δx dy 与 dx ,分别称为自变量 x 与 函数 y 的 微分。 dy = f (x)dx —— 微分问题

泛函的变分variation of functional U=U[y(x)】 H(为 函数y有一微小变化: △y=y-y=y 泛函U也有一增量: △U=U[y(x)】-U[y(x)】=6U 函数的增量⊙y、泛函的增量U等 称为变分。 研究函数的变化与泛函的增量之间的关系称为变分问题
泛函的变分 variation of functional U U y x ( ) 函数 y 有一微小变化: 1 y y y 泛函 U 也有一增量: y 1 U U y x U y x ( ) ( ) U 函数的增量y 、泛函的增量 U 等 称为变分。 研究函数的变化与泛函的增量 之间的 关系称为变分问题
变分问题例子:最速下降问题 质点受重力作用从A到B沿曲线路径自由下滑,不考虑摩擦 力,求质点下降最快的路径。 40,0) P(x,y) B1) ro- 图7.1
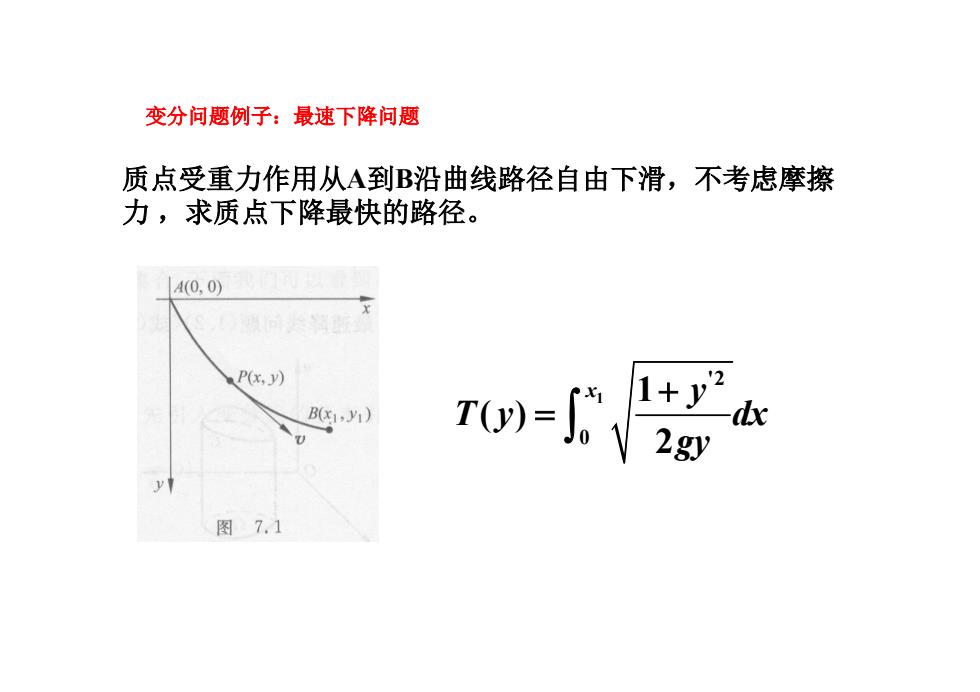
变分问题例子:最速下降问题 质点受重力作用从A到B沿曲线路径自由下滑,不考虑摩擦 力 ,求质点下降最快的路径。 1 '2 0 1 ( ) 2 x y T y dx gy

函数的极值: 若 y=f(x) 在X。处有极值, 则有: f'(x=0 泛函的极值 若Uy]在yx)处有极值, 则有: 6U[y(x)=0
函数的极值: 若 y f x ( ) 在 x0 处有极值, 则有: 0 ( ) 0 x f x 泛函的极值 若 U[y(x)] 在 y0(x) 处有极值, U y x ( ) 0 则有:

用泛函的极值问题表示的原理称为变分原理。 普通的动力学原理直接研究真实的状态,然后得到状态所 应满足的方程。而变分原理则不然,它不是专注于实际的 状态,而是考察约束所容许的一切可能的状态,根据真实 状态所满足的变分条件(如:真实位移使势能取极值,势 能变分为零),进而得到真实状态所应满足的方程。 真实变形曲线
用泛函的极值问题表示的原理称为变分原理。 普通的动力学原理直接研究真实的状态,然后得到状态所 应满足的方程。而变分原理则不然,它不是专注于实际的 状态,而是考察约束所容许的一切可能的状态,根据真实 状态所满足的变分条件(如:真实位移使势能取极值,势 能变分为零),进而得到真实状态所应满足的方程。 真实变形曲线 {F}