
第三章能量原理及其应用(9) §3.1弹性体的功与应变能(2) §3.2虚功原理(1) §3.3单位载荷法(2) §3.4泛函与变分简介(1) §3.5最小势能原理(2) §3.6基于能量原理的近似解法(1)
第三章 能量原理及其应用(9) §3.1 弹性体的功与应变能(2) §3.2 虚功原理 (1) §3.3 单位载荷法 (2) §3.4 泛函与变分简介 (1) §3.5 最小势能原理 (2) §3.6 基于能量原理的近似解法 (1)

§3.1弹性体的功与应变能 ■当弹性体受到外力作用时,它就发生变形,因 而外力在变形位移方向上对弹性体做功。 ■如果不计及弹性体在加载和卸载时能量的损失 ,即当结构系统是保守系统,则对这样的物体 在变形时所做的功,可以看成是储存在物体中 的能量,称为应变能(strain energy)。因此, 应变能可以看成是弹性体变形时,它所吸收的 能量
当弹性体受到外力作用时,它就发生变形,因 而外力在变形位移方向上对弹性体做功。 如果不计及弹性体在加载和卸载时能量的损失 ,即当结构系统是保守系统,则对这样的物体 §3.1 弹性体的功与应变能 ,即当结构系统是保守系统,则对这样的物体 在变形时所做的功,可以看成是储存在物体中 的能量,称为应变能(strain energy)。因此, 应变能可以看成是弹性体变形时,它所吸收的 能量
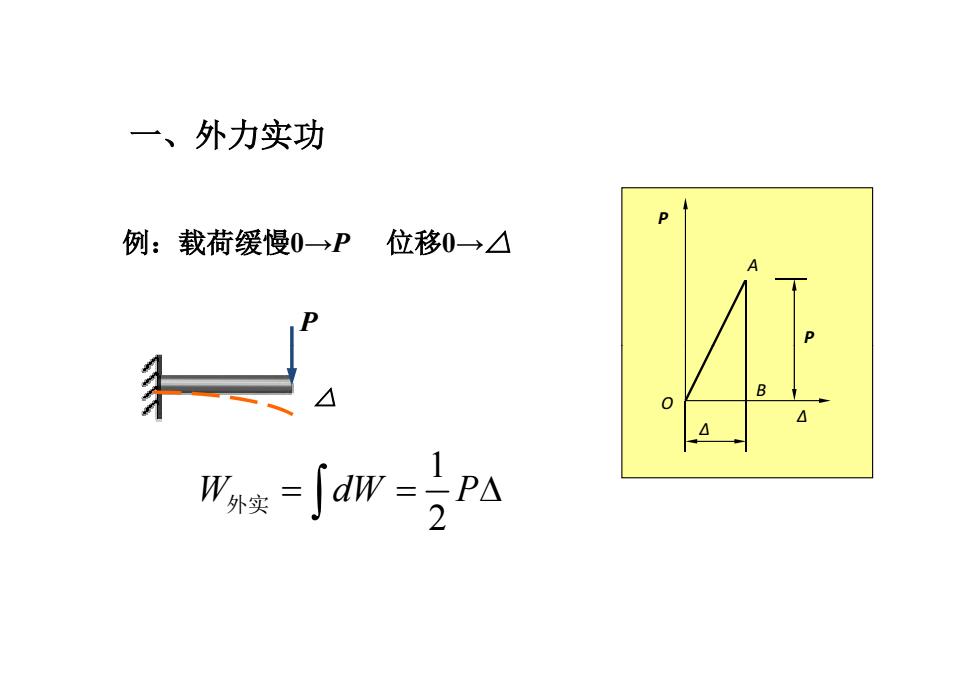
一、外力实功 例:载荷缓慢0→P 位移0△ B 0 W∫w-Pa
一、外力实功 P A P 例:载荷缓慢0→P 位移0→△ P Δ O B Δ P △ 1 2 W dW P 外实

M A新 1 W外实 MO 2 外力实功:广义力与方向广义位移乘积的一半
A y M 1 2 W M 外实 外力实功:广义力与方向广义位移乘积的一半

在线弹性范围内,外力由零开始缓慢增加到某一值, 将外力做的实功统一写成 1 W外实2 F△ 式中F一一广义力; △一一与广义力对应的位移,即为广义力作 用点且与广义力方向一致的位移。称为广义位 移
在线弹性范围内,外力由零开始缓慢增加到某一值, 将外力做的实功统一写成 式中 F——广义力; 1 = 2 W F 外实 Δ——与广义力对应的位移,即为广义力作 用点且与广义力方向一致的位移。称为广义位 移