第七章弯曲变形 计并银公移的积分信 2.连续条件分段处挠曲线所应满足的连续、光 滑条件,简称为梁位移的连续条件。 b 0c左=8ci Wc左=WC右 ⊙嘉大兽
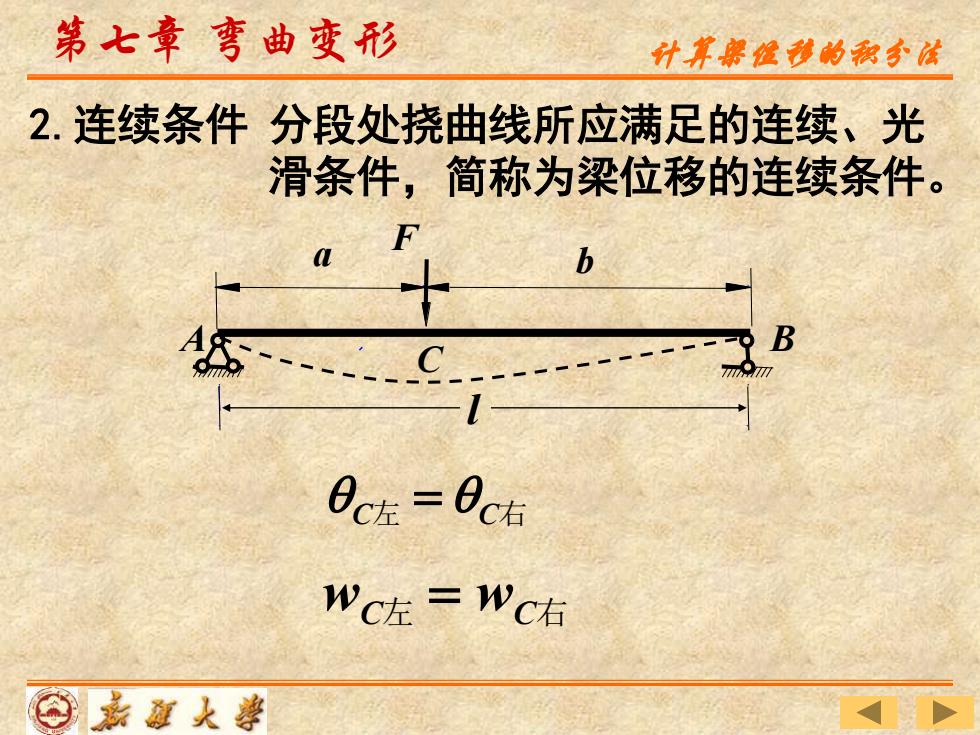
2.连续条件 第七章 弯曲变形 A B F a b C l 分段处挠曲线所应满足的连续、光 滑条件,简称为梁位移的连续条件。 wC左 = wC右 C左 = C右 计算梁位移的积分法

第七章弯曲变形 计其眼任移的积分店 讨论:画挠曲线大致形状 依据: d'w M(x) 少 约束条件; dx? EI >载荷情况,作出M图; >凹凸情况一由w"即M的正负号决定 M>0,凹; M<0,凸; 一」 段M=0,直线;一点M=0,拐点 >光滑连续特性
讨论: 画挠曲线大致形状 依据: ➢ 约束条件; ➢ 载荷情况,作出M 图; ➢ 凹凸情况——由w″即M 的正负号决定 M>0,凹; M<0,凸; 一段M= 0,直线;一点M= 0,拐点 ➢ 光滑连续特性。 EI M( x ) dx d w 2 2 = 第七章 弯曲变形 计算梁位移的积分法
第七章弯曲变形 计其架雀移的积分底 例题7-1 悬臂梁受力的大小和方向如图示。试绘制挠 曲线的大致形状 Fa = 2 人鑫 2-G C 解: M Fa X Fa 拐点 B C 直线 凸曲线 B 凹曲线 ⊙嘉火
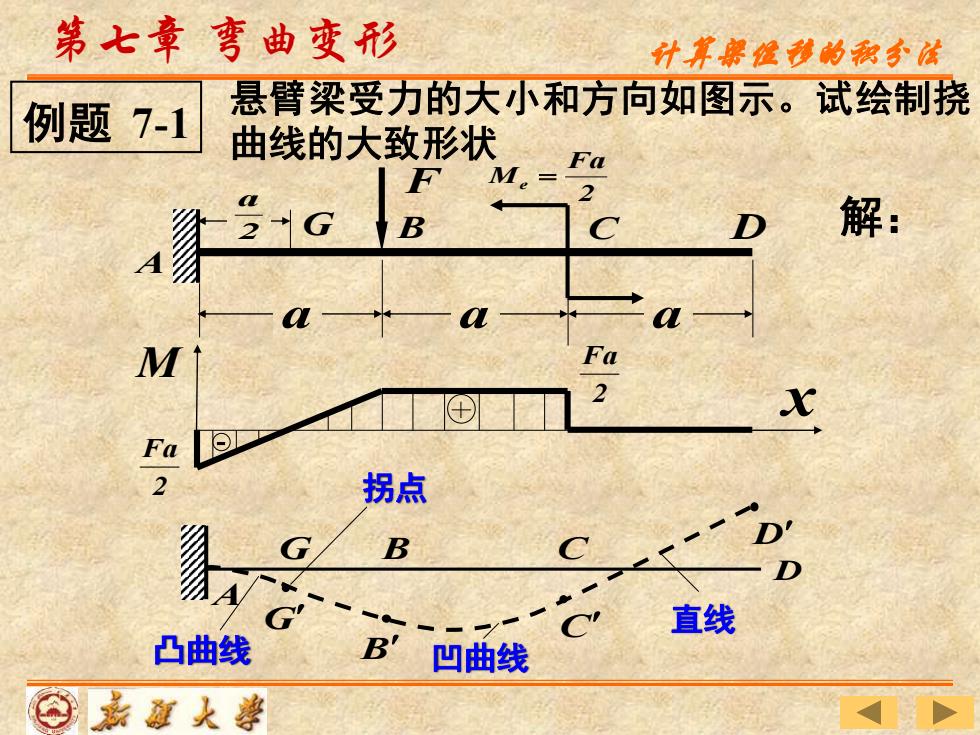
第七章 弯曲变形 M 2 x Fa 2 Fa G B C A G B C D 凸曲线 拐点 凹曲线 直线 悬臂梁受力的大小和方向如图示。试绘制挠 曲线的大致形状 2 G a a a a A B C D F 2 Fa Me = D 解: 计算梁位移的积分法 例题 7-1
第七章弯曲变形 计其解怪移的积分依 例题7-2求图示悬臂梁的转角方程0=日似)和挠度方 1 wc),并求最大转角日max及最大挠度wmax。 梁在竖直平面内弯曲时的抗弯刚度EI为已知。 w M B 解:1. 建立坐标系 2.求支反力F4=F M=FI 3.列弯矩方程M(x)=F(1-x) ⊙嘉面人善
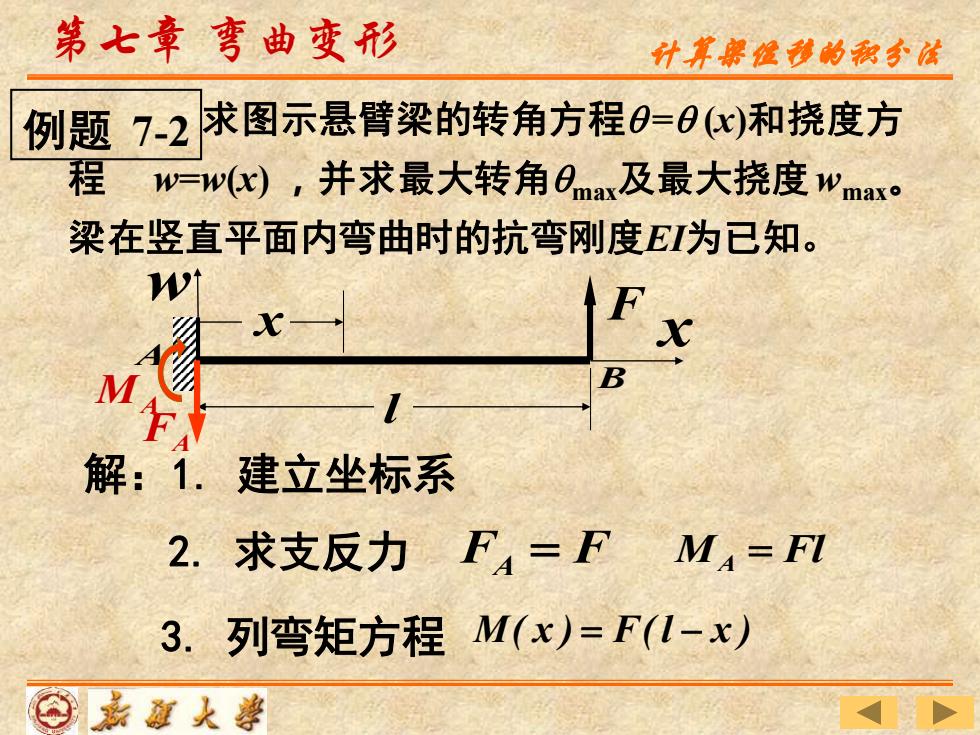
第七章 弯曲变形 求图示悬臂梁的转角方程 = (x)和挠度方 程 w=w(x) ,并求最大转角max及最大挠度wmax。 梁在竖直平面内弯曲时的抗弯刚度EI为已知。 l A B w x x 解:1. 建立坐标系 2. 求支反力 FA MA FA = F M Fl A = 3. 列弯矩方程 M( x ) = F(l − x ) 计算梁位移的积分法 例题 7-2 F

第七章弯曲变形 计并解任移的积分店 W F X B 4.建立挠曲线近似微分方程并积分 EIw"(x)=F(I-x) x Ehe(x)-E1O-F(-)4C Elw(x)-F( 5.确定积分常数 26+C+D 边界条件 在x=0处,0=0,求得:C=0, w=0 D=0 ⊙嘉范大事
第七章 弯曲变形 l A B w x x 4. 建立挠曲线近似微分方程并积分 EIw ( x ) = F(l − x ) ) C 2 x EIw ( x ) EI F(l x 2 = = − + ) Cx D 6 x 2 l x EIw( x ) F( 2 3 = − + + 5. 确定积分常数 边界条件 在x = 0 处 , θ = 0 , w = 0 求得:C = 0 , D= 0 计算梁位移的积分法 F