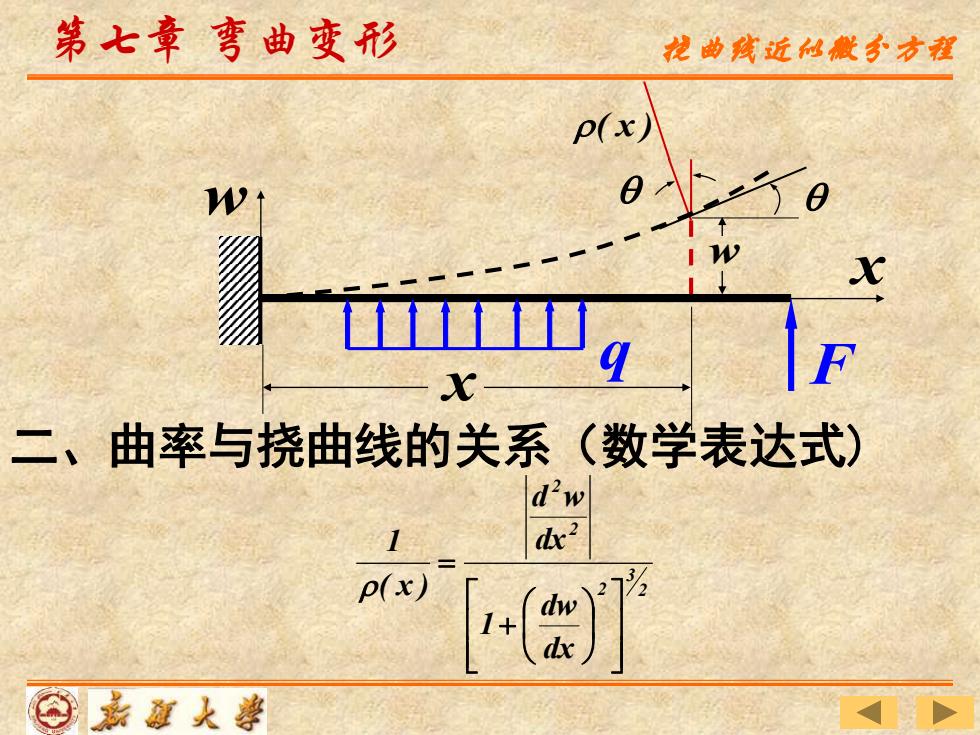
第七章弯曲变形 龙曲残近仙微今方程 p(x) I W x x 二、曲率与挠曲线的关系(数学表达式) dw p(x) 1+ dw ⊙嘉道人薯
w 第七章 弯曲变形 q F x x w ( x ) 二、曲率与挠曲线的关系(数学表达式) 2 3 2 2 2 dx dw 1 dx d w ( x ) 1 + = 挠曲线近似微分方程
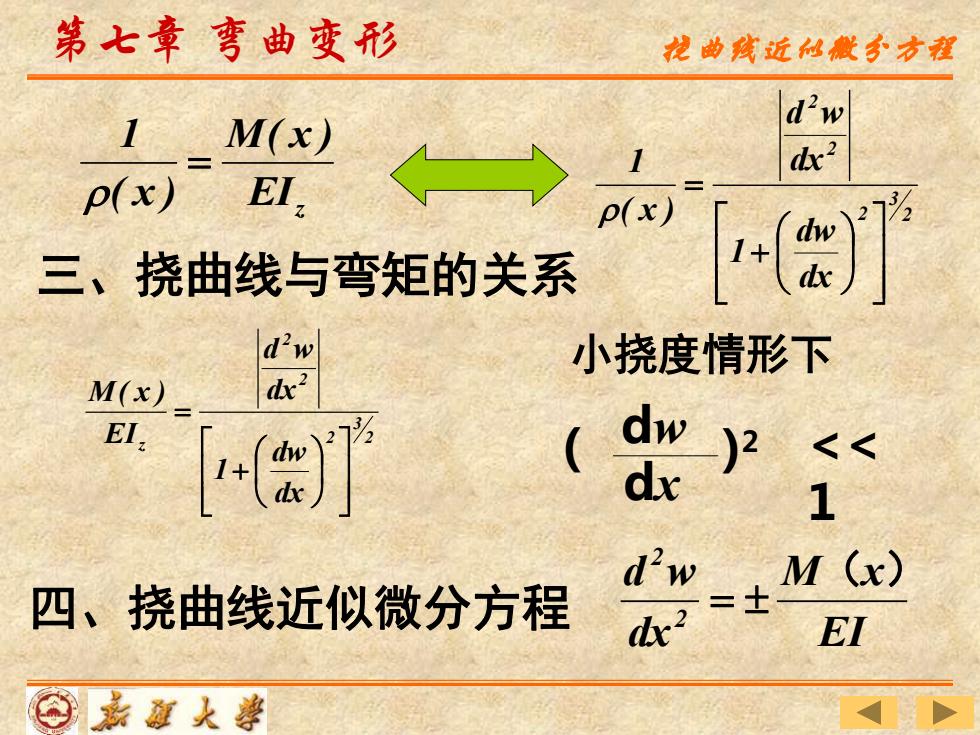
第七章弯曲变形 龙曲孩近仙微分方程 1 M(x) p(x) EI, 三、挠曲线与弯矩的关系 小挠度情形下 M(x) EI, dw << dv 2 1 d'w M(x) 四、挠曲线近似微分方程 =士 dx2 EI ⊙嘉范大事
第七章 弯曲变形 2 3 2 2 2 dx dw 1 dx d w ( x ) 1 + = z EI M( x ) ( x ) 1 = 三、挠曲线与弯矩的关系 2 3 2 2 2 z dx dw 1 dx d w EI M( x ) + = 小挠度情形下 ( dw dx ) 2 << 1 EI M x dx d w 2 2 ( ) 四、挠曲线近似微分方程 = 挠曲线近似微分方程
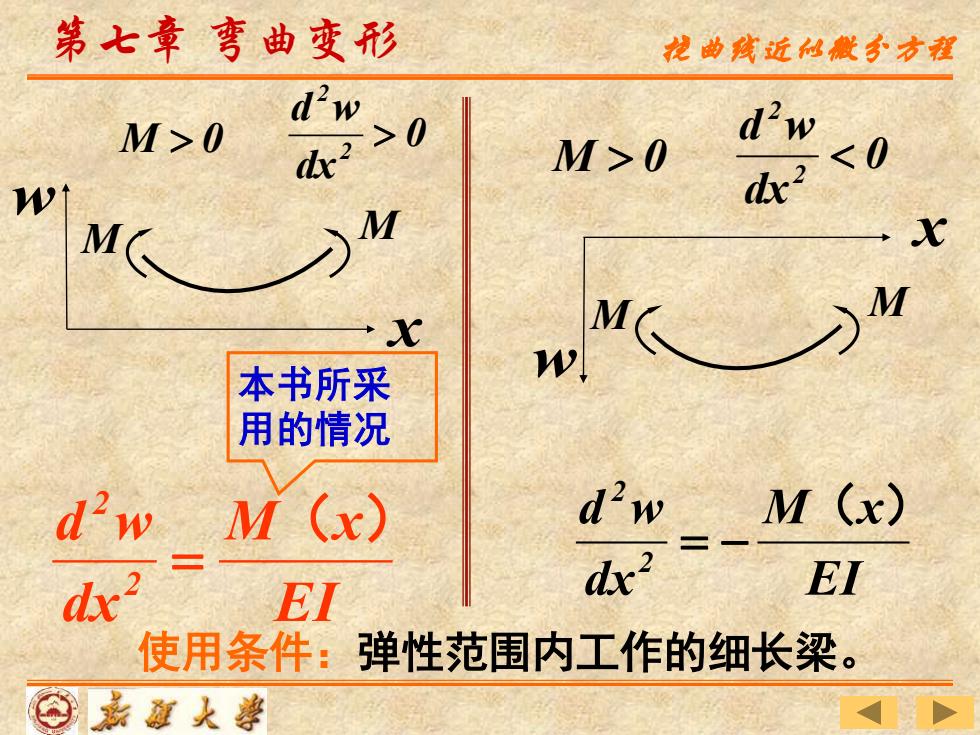
第七章弯曲变形 花曲孩近仙撒今方程 M>0 d'w-0 dx2 M>0 <0 dx2 X 本书所采 用的情况 d2w M(x) dwM(x) EI EI 使用条件:弹性范围内工作的细长梁。 ⊙嘉面人妻
EI M x dx d w 2 2 ( ) = − EI M x dx d w 2 2 ( ) = M 0 M 0 本书所采 用的情况 w x M M w x 使用条件:弹性范围内工作的细长梁。 M M 第七章 弯曲变形 挠曲线近似微分方程 0 dx d w 2 2 0 dx d w 2 2

第七章弯曲变形 计并银公移的积分信 §7-3计算梁位移的积分法 一、积分法 d2w M(x) EIw"(x)=M(x) 2 EI Ew(x)=∫M(x)&+C Ew(x)=∫(M(xxx+Cx+C, 利用梁的位移条件确定式中的积分常数,就得转角 方程0=0x)=w′(x)和挠度方程w=w(x),从而也就 可以求某个具体横截面处的转角和挠度了。这种求转 角和挠度的方法称为积分法。 ⊙嘉大票
第七章 弯曲变形 §7-3 计算梁位移的积分法 一、积分法 EIw(x) = M(x) dx C1 EIw ( x ) = M( x ) + dx C1 x C2 EIw( x ) = ( M( x )dx ) + + 利用梁的位移条件确定式中的积分常数,就得转角 方程 = (x) = w′(x)和挠度方程w = w (x) ,从而也就 可以求某个具体横截面处的转角和挠度了。这种求转 角和挠度的方法称为积分法。 计算梁位移的积分法 EI M x dx d w 2 2 ( ) =
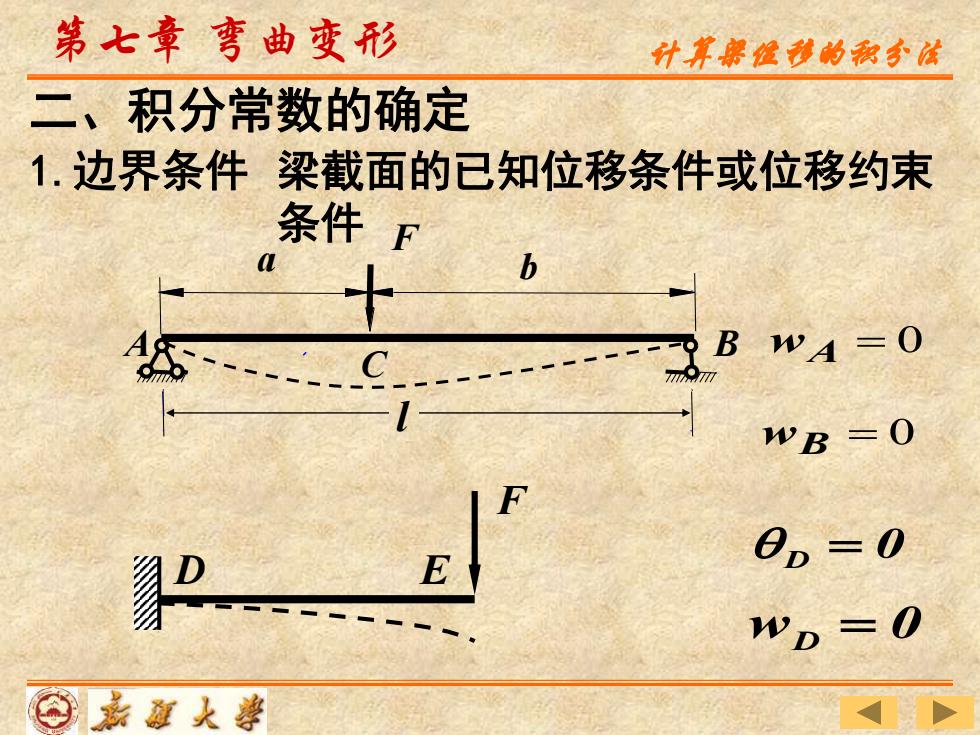
第七章弯曲变形 计其解怪移的积分依 二、积分常数的确定 1.边界条件梁截面的已知位移条件或位移约束 条件 F B W=0 WB=0 E OD-0 WD =0 ⊙嘉面人¥
梁截面的已知位移条件或位移约束 条件 二、积分常数的确定 1.边界条件 第七章 弯曲变形 A B F a b C l wA = 0 wB = 0 wD = 0 D = 0 D E F 计算梁位移的积分法