
7.1绪论 4)PID神经元网络(PIDNN)的特点和结构形式 PIDNN的主要特点如下; ■PIDNN属于交层前向神经元网络; ■PIDNN参照PID控制规律构成,结构比较简单、规范。 ■PIDNN的初值按PID控制规律的基本原侧确定,加快了 收敛速度,不易陷入极小点,更重要的是可以利用现有 的PID控制的大量经验数据确定网络权重初值,使控制 系统保持初始稳定,使系统的全局稳定成为可能。 PIDNN可采用"无教师”的学习方式,根据控制效果进 行在线自学习和调整,使系统具备较好的性能。 ■PIDNN可同时适用于SISO以及MIMO控制系统
7.1 绪论 4)PID神经元网络(PIDNN)的特点和结构形式 PIDNN的主要特点如下; ◼ PIDNN属于交层前向神经元网络; ◼ PIDNN参照PID控制规律构成,结构比较简单、规范。 ◼ PIDNN的初值按PID控制规律的基本原则确定,加快了 收敛速度,不易陷入极小点;更重要的是可以利用现有 的PID控制的大量经验数据确定网络权重初值,使控制 系统保持初始稳定,使系统的全局稳定成为可能。 ◼ PIDNN可采用“无教师”的学习方式,根据控制效果进 行在线自学习和调整,使系统具备较好的性能。 ◼ PIDNN可同时适用于SISO以及MIMO控制系统
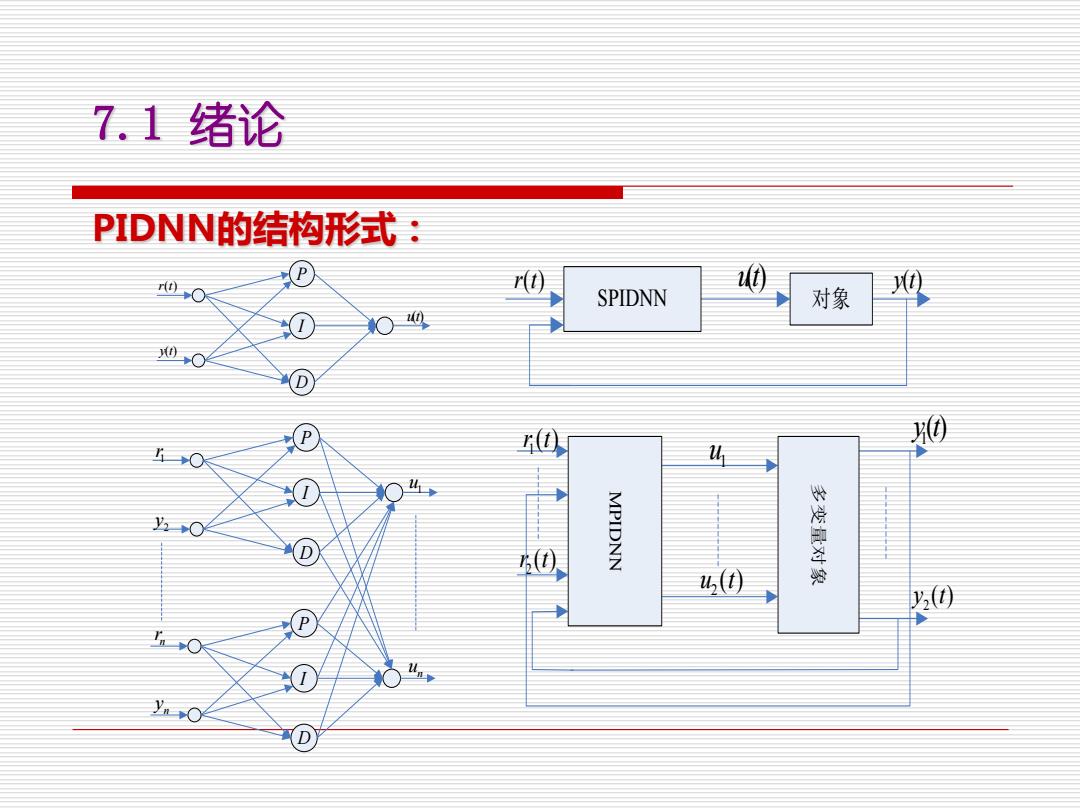
7.1绪论 PIDNN的结构形式: P r(1) ⑩ SPIDNN 对象 ① D u MPIDNN u(t) (0 yO
PIDNN的结构形式: 7.1 绪论 P ID rt() yt() ut() r t( ) ut() yt( ) SPIDNN 对象 P ID P ID 1r 2 y n r n y 1 u n u 1r t( ) 1 u 2r t( ) 2 u t( ) 2 y t( ) 1yt() MPIDNN 多变量对象

7,2PID神经元的计算方法 1)比例元 O比例元的输入为4因=冕,W ② 比例元的状态函数4,()=net,( ③比例元的输出函数 1 u()>1 向=以优】=u() -1≤u()≤1 -1 u,(份<-1
7.2 PID神经元的计算方法 ① 比例元的输入为 1 1 ( ) ( ) n j ij i j net k w x k − = = 1) 比例元 ② 比例元的状态函数 ( ) ( ) j j u k net k = ③ 比例元的输出函数

7.2PID神经元的计算方法 2)积分元 u(k)=g,[net,(k),u,(k-1]=u,(k-1)+net (k) 积分元的输入和输出函数与比例函数相同。 3)微分元 u,(k)=golnet,(k),net (k-1]=net (k)-net (k-1) 微分元的输入和输出函数与比例函数相同
7.2 PID神经元的计算方法 2) 积分元 ( ) [ ( ), ( 1)] ( 1) ( ) j I i j j j u k g net k u k u k net k = − = − + 积分元的输入和输出函数与比例函数相同。 3) 微分元 ( ) [ ( ), ( 1)] ( ) ( 1) j D j j j j u k g net k net k net k net k = − = − − 微分元的输入和输出函数与比例函数相同

7.3PID神经元网络 将PID和一般神经元网络融合起来的方法包括两个步骤: ①将PID功能引入神经网络的神经元中,构成PID神经元 (第二节完成); ②. 按照PID神经元的控制规律的基本模式,用这些基本神 经元构成新的神经元网络,并找到合理有效的计算与学 习方法(下节完成)
7.3 PID神经元网络 将PID和一般神经元网络融合起来的方法包括两个步骤: ① 将PID功能引入神经网络的神经元中,构成PID神经元 (第二节完成); ② 按照PID神经元的控制规律的基本模式,用这些基本神 经元构成新的神经元网络,并找到合理有效的计算与学 习方法(下节完成)