
放射学院 精品课程 二、实验误差的表示方法 为了表示误差,工程上引用了精密度、准确度和精确度的概念。精密度表示测量结果的重演程度,精密 度高代表随机误差小:准确度指测量结果的正确性,准确度高表示系统误差小:精路度(又称精度)包含精 密度和准确度的含义,精确度高表示测量结果既精密又可靠。利用任何量具或仪器进行测量时,总存在误差 测量结果总不可能准确地等于被测量的真值,而只是它的近似值。测量的质量高低以测量精确度作指标 据测量误差的大小来估计测量的精确度。测量结果的误差愈小,则认为测量就愈清确。误差的表示方法有下 面几种, 1.绝对误差测量伯和真值之差为绝对误差,通常称为误差。记为: 12.51 由于真值一般无法求得,因而上式只有理论意义。常用高一级标准仪器的示值作为实际值以代替真值 由于高一级标准仪器存在较小的误差,因而A不等于,但总比更接近于。与之差称为仪器的示值绝对误差。 记为 (2-6) 与d相反的数称为修正值,记为 2-7 通过检定,可以由高一级标准仪器给出被检仪器的修正值。利用修正值便可以求出该仪器的实际值。即 (2-8) 绝对误差反映测量的准确度,又反映测量的精确度。 2相对误差衡量某一测量值的准确程度,一般用相对误差来表示。示值绝对误差与被测量的实际值的百 分比值称为实际相对误差。记为 (2.9) 以仪器的示值代替实际值的相对误差称为示值相对误差。记为 (2-10) 一般来说,除了某些理论分析外,用示值相对误差较为适宜。相对误差既反映测最的准确度,又反映测 范围。在某些实验测量及数据处理中,不能从误差的绝对值来衡量数据的精确程度,因为精确度与测量数据 大小的本身也很有关系。例如在测量电压时,如果数据接近100kW,精确到1000V就够了,这时的绝对误 差是1000V,其相对误差仅1%。果测量的电压不过1000V,绝对误差是20V,其相对误差就是2%。由 此可见,虽然后者的绝对误差是前者的1/50,但相对误差却是前者的2倍。 3.引用误差为了计算和划分仪表精确度等级,提出引用误差概念。其定义为仪表示值的绝对误差与量程 范围之比。 2-11 ,示值绝对误差:标尺上限值-标尺下限值。 4算术平均误差算术平均误差是各个测量点的误差的平均值 2-12) ,测量次数:为第次测量的误差 5.标准误差标准误差亦称为均方根误差。其定义为 (2-13) 上式使用于无限测量的场合。实际测量工作中,测量次数是有限的,则改用下式 2.14 标淮误差不是 一个具体的误差,的大小只说明在 一定条件下等精度测量集合所属的每一个观测值对其算术 平均值的分散程度,如果的值愈小则说明每一次测量值对其算术平均值分散度就小,测量的精度就高,反之 精度就低。 -16-

放射学院 精品课程 三、数据处理方法 1误差的基本性质在实验中通常直接测量或间接测量得到有关的参数数据,这些参数数据的可靠程度如 何?如何提高其可靠性?因此,必须研究在给定条件下误差的基本性质和变化规律。 (1)误差的正态分布:如果测量数列中不包括系统误差和过失误差,从大量的实验中发现偶然误差的大 小有如下几个特征:①绝对值小的误差比绝对值大的误差出现的机会多,即误差的概率与误差的大小有关 这是误差的单峰性:②绝对值相等的正误差或负误差出现的次数相当,即误差的概率相同。这是误差的对利 性:③极大的正误差或负误差出现的概率都非常小,即大的误差一般不会出现。这是误差的有界性:④随若 测量次数的增加,偶然误差的算术平均值趋近于零。这叫误差的低偿性。 图2-2误差分布曲 根据上述的误差特征,可疑的出误差出现的概率分布图,如图2-2所示。图中横坐标表示偶然误差,纵 坐标表示个误差出现的概率,图中曲线称为误差分布曲线,以表示。其数学表达式有高斯提出,具体形式为: (2-15) (2-16) 上式称为高斯误差分布定律亦称为误差方程。式中σ为标准误差,h为桔确度指数,。和h的关系为 (2-17) 若误差按函数关系分布,则称为正态分布。。越小,测量精度越高,分布曲线的峰越高切窄:。越大, 分布曲线越平坦且越宽,如图2-3所示。由此可知,¤越小,小误差占的比重越大,测量精度越高。反之 则大误差占的比重越大,测量精度越低。 图23不同σ的误差分布曲线 (2)测量集合的最佳值:在测量精度相同的情况下,测量一系列观测值,所组成的测量集合,假 设其平均值为,则各次测量误差为 i=1 当采用不同的方法计算平均值时,所得到误差值不同,误差出现的概率亦不同。若选取适当的计算方法。 使误差最小,而概率最大,由此计算的平均值为最佳值。根据高斯分布定律,只有各点误差平方和最小,才 能实现概率最大。这就是最小乘法值。由此可见,对于一组精度相同的观测值,采用算术平均得到的值是该 组观测值的最佳值。 2.有限测量次数中标准误差σ的计算:由误差基本概念知,误差是观测值和真值之差。在没有系统误差 存在的情况下,以无限多次测量所得到的算术平均值为真值。当测量次数为有限时,所得到的算术平均值近 似于真值,称最佳值。因此,观测值与真值之差不同于观测值与最佳值之差。 令真值为A,计算平均值为a,观测值为M,并令d=M-a,D=M-A,则 因为 代入中,即得 (2-18 将式(2-23)式代入d=Ma中得 .17-
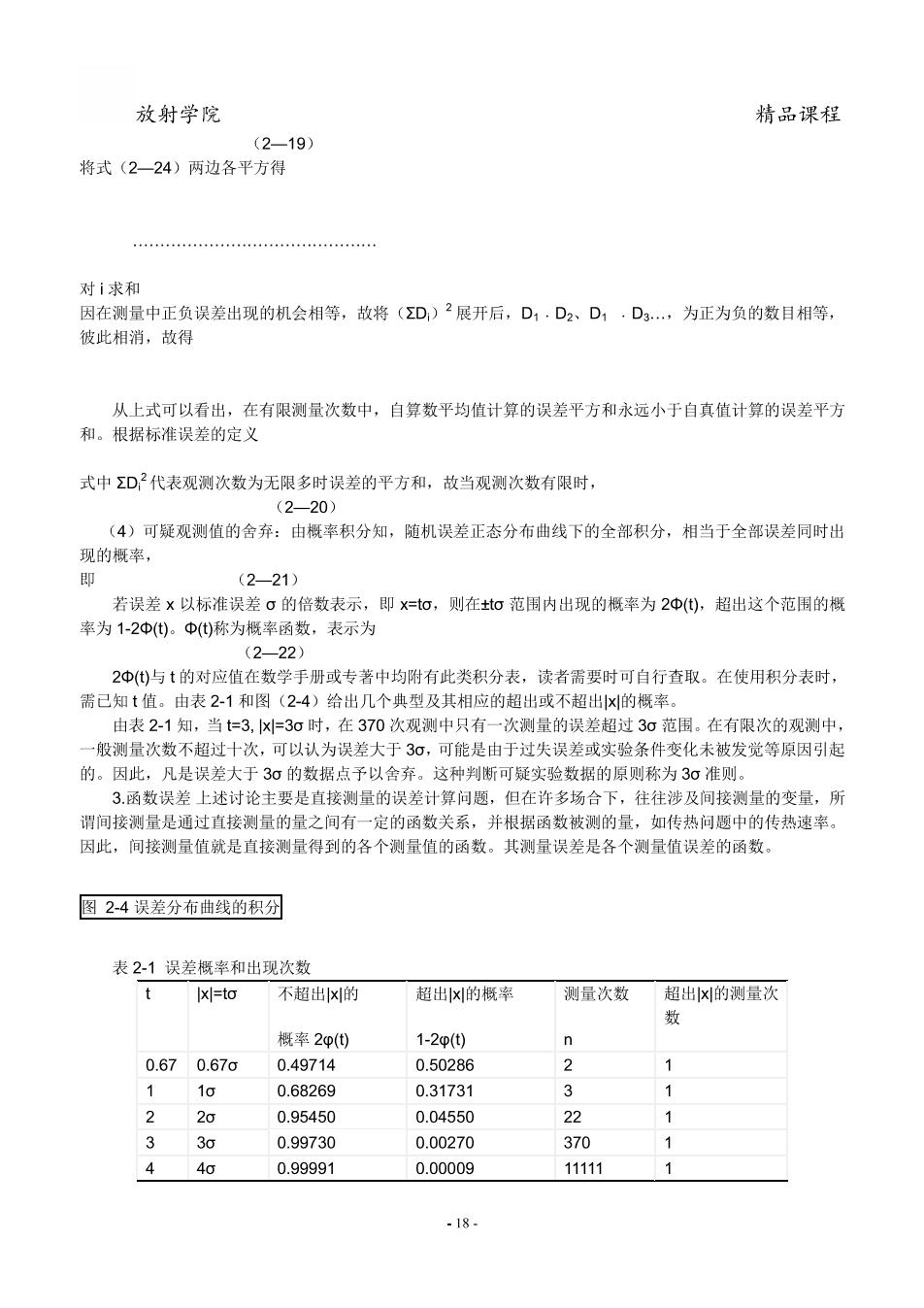
放射学院 精品课程 (2-19 将式(2-24)两边各平方得 对i求和 因在测量中正负误差出现的机会相等,故将(D)2展开后,D1·D2、D1.Dg,为正为负的数目相等, 彼此相消,故得 从上式可以看出,在有限测量次数中,自算数平均值计算的误差平方和永远小于自真值计算的误差平方 和。根据标准误差的定义 式中D代表观测次数为无限多时误差的平方和,故当观测次数有限时, 2—20 (4)可疑观测值的舍弃:由概率积分知,随机误差正态分布曲线下的全部积分,相当于全部误差同时出 现的概率, 即 (2-21) 若误差×以标准误差σ的倍数表示,即×=o,则在±o范围内出现的概率为2中(),超出这个范围的概 率为1-2)。()称为概率函数,表示为 (2—22) 2中()与t的对应值在数学手册或专著中均附有此类积分表,读者需要时可自行查取。在使用积分表时, 需己知t值。由表2-1和图(24)给出几个典型及其相应的超出或不超出x的概率。 由表21知,当3,x30时,在370次观测中只有一次测量的误差超过30范围。在有限次的观测中 般测量次数不超过十次,可以认为误差大 30, 可能是由于过失误差或实验条件变化未被发觉等原因引志 的。因此,凡是误差大于30的数据点予以舍弃。这种判断可疑实验数据的原则称为30准则 3函数误差上述讨论主要是直接测量的误差计算问题,但在许多场合下,往往涉及间接测量的变量,所 谓间接测量是通过直接测量的量之间有一定的函数关系,并根据函数被测的量,如传热问题中的传热速率。 因此,间接测量值就是直接测量得到的各个测量值的函数。其测量误差是各个测量值误差的函数。 图2-4误差分布曲线的积分 表21误差概率和出现次数 t x|=to 不超出x的 超出x的概率 测量次数 超出x的测量次 概率2p() 1-2φ() n 0.670.67o 0.49714 0.50286 2 1 1 0.68269 0.31731 3 1 2 20 0.95450 0.04550 22 3 30 0.99730 0.00270 370 1 440 0.99991 0.00009 11111 1 -18

放射学院 精品课程 1)函数误差的一般形式:在间接测量中,一般为多元函数,而多元函数可用下式表示: y=f(x1,X2X)) (2-23) 式中y:间接测量值:x:直接测量值。 由台劳级数展开得 2-24 它的最大绝对误差为 (2-25) 式中:误差传递系数:△x:直接测量值的误差:△y:间接测量值的最大绝对误差。 函数的相对误差δ为 (2-26) 2)某些函数误差的计算:①函数y=X士z绝对误差和相对误号 由于误差传递系数,则函数最大绝对误差 Ay=±(Iax+1az (2-27 相对误差 (2-28) ②函数形式为,X、乙、w为变量,误差传递系数为: 函数的最大绝对误差为 (2-29 函数的最大相对误差为 (2-30) 现将某些常用函数的最大绝对误差和相对误差列于表2-2中。 表2-2某些函数的误差传递公式 误差传递公式 函数式 最大绝对误差 最大相对误差 各变量的绝对误差为 .19

放射学院 精品课程 各变量的误差传递系数为 函数的绝对误差 70000a0e1o412i030s4901a8n100o5 =3.52×103×0.2-1.41×102×0.02+0.206x0.02-1 =4.00×103J(gK J/(g-K) 枚真值C,-0.8798±0.0003gK 由有效数字位数考虑以上的测量结果清度已满足要求。若不仅考虑有效数字位数,尚需从比较各变量的 测量精度,确定是否有可能提高测量精度。则可从分析比较各变量的相对误差着手。各变量的相对误差分别 为 其中以60的相对误差为0.468%,误差最大,是M的5.85倍,是m的14.63倍。为了提高Cp的测量精度 可改善的测量仪表的精度,即提高测量计的精度。由此可见,变量的精度基本相当。提高0精度后C。的 绝对误差为 △C=3.52×103×0.2-1.41×102×0.02+0.206×0.002-1.08×102×0.05 =-0.704×103.0.282×103+0.412x1030.54×103 =2.94×104JgK) 系统提高精度后,Cp的真值为:C=0.8798±0.0003J(gK) 4.系统误差的判断在系统误差比偶然误差更为显著的情况下,可根据下列方法判断是否存在系统误差 (1)实验对比法:如改变产生系统误差的条件,进行对比测量,可用以发现系统误差。这种方法适用于 发现不变的系统误差。例如 在称 时存在若出于砝码质 不 维而产生的不变系统误 这 误差多次重复 测量不能被发现,只有用高一级精度的砝码进行对比称量时,才能发现它。在测量温度、压力、电阻等物理 量中都存在若同样的问题。 (2)数据统计比较法:对同一物理量进行二组(或多组)独立测量,分别求出它们的平均值和标准误差,判 断是否满足偶然误差的条件来发现系统误差。 5.系统误差的估算在有些实验中,可估算由于改变某一因素而引入的系统误差,这对于分析系统误 差的主要来源有参 考价值。例如 在测定气体摩尔质量时,可推算由于采用理想气体状态方程所引入的系统 误差:在凝固点降低法测摩尔质量时,可推算由于加入品种而引起的系统误差:在蔗糖转化动力学实验中, 可推算由于反应温度偏离所造成的系统误差等。 6.系统误差的减小和消除在测量过程中,如存在若较大的系统误差、必须认直找出产生系统误差的因 素,并应尽力设法消除成减小之。 (1)消除产生系统误差的根源:从产生误差的根源上消除系统误差是最根本的方法。它要求实验者 测量过程中可能产生系统误差的各种环节作仔细分析,找出原因并在测量前加以消除。如为了防止仪器的调 整误差,在测量前要正确和严格地调整仪器。例如,天平的水平调整、测高仪的垂直度调整等。又如,为了 防止测量过程中仪器零点变动,在测量开始和结束时,都需检查零点。再如,为了防止经长期使用导致仪器 精度降低,就要定期进行严格的检定与维护, 如果系统误差是由外界条件变化引起的,应在外界条件比较稳定时进行测量 (②)采用修正法消除系统误差:这种方法是预先将仪器的系统误差检定出来或计算出来,做出误差表或 误差曲线,然后取与误差数值大小相同、符号相反的值作为修正值,进行误差修正。即 -20-