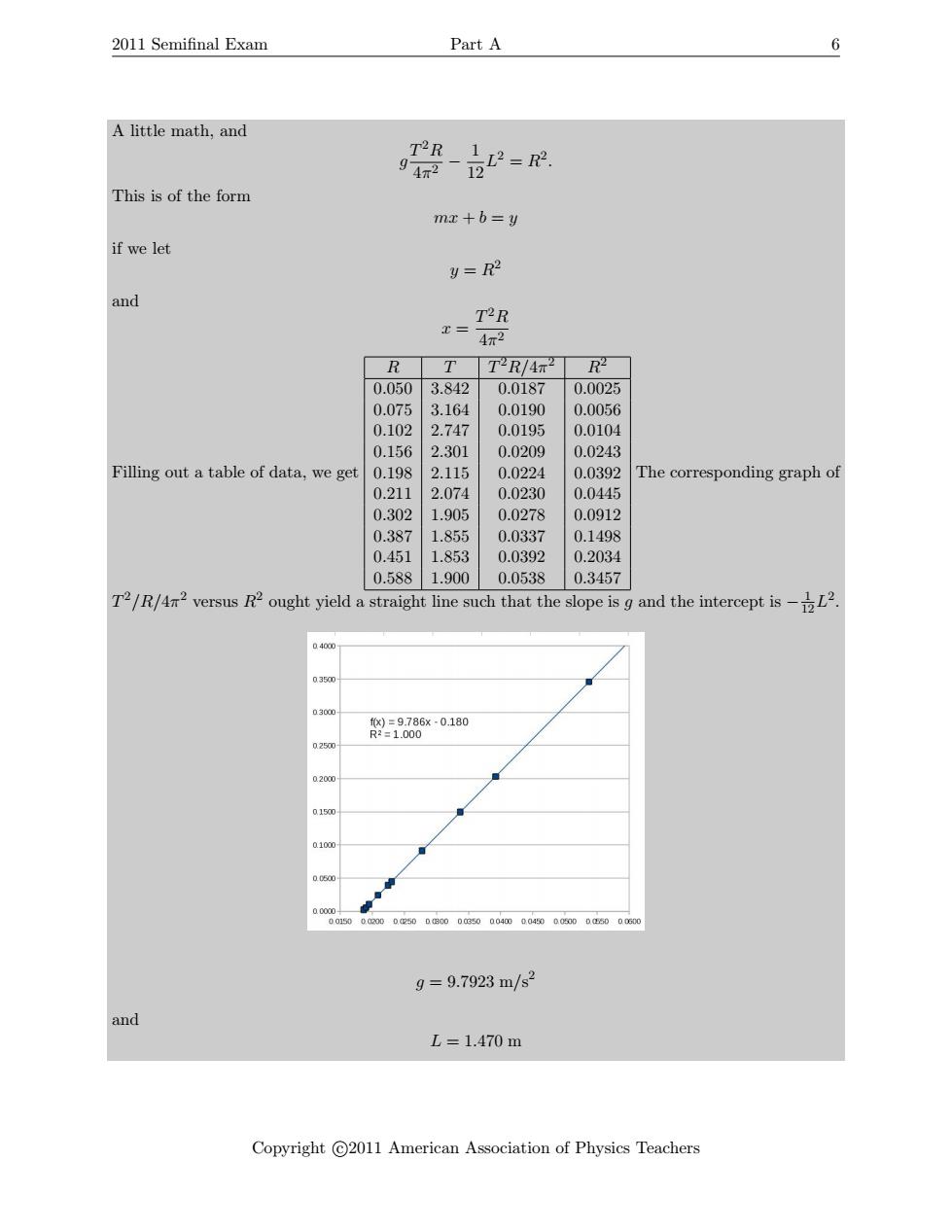
2011 Semifinal Exam Part A 6 A little math,and T2R 12=R2 94r2- 12 This is of the form mx +b=y if we let y=R2 and T2R T= 4r2 R T T2R/4R2 R 0.050 3.842 0.0187 0.0025 0.075 3.164 0.0190 0.0056 0.102 2.747 0.0195 0.0104 0.156 2.301 0.0209 0.0243 Filling out a table of data,we get 0.198 2.115 0.0224 0.0392 The corresponding graph of 0.211 2.074 0.0230 0.0445 0.302 1.905 0.0278 0.0912 0.387 1.855 0.0337 0.1498 0.451 1.853 0.0392 0.2034 0.588 1.900 0.0538 0.3457 T2R42 versus R2ought yield a straight line such that the slope isg and the intercept is 04000 0.3500 0300 f0)=9.786x-0.180 R2=1.000 02500 02000 01500 0.100 00500 001500030002500s0000g5000400.045000000.a5000G00 9=9.7923m/s2 and L=1.470m Copyright C2011 American Association of Physics Teachers
2011 Semifinal Exam Part A 6 A little math, and g T 2R 4π 2 − 1 12 L 2 = R 2 . This is of the form mx + b = y if we let y = R 2 and x = T 2R 4π 2 Filling out a table of data, we get R T T 2R/4π 2 R2 0.050 3.842 0.0187 0.0025 0.075 3.164 0.0190 0.0056 0.102 2.747 0.0195 0.0104 0.156 2.301 0.0209 0.0243 0.198 2.115 0.0224 0.0392 0.211 2.074 0.0230 0.0445 0.302 1.905 0.0278 0.0912 0.387 1.855 0.0337 0.1498 0.451 1.853 0.0392 0.2034 0.588 1.900 0.0538 0.3457 The corresponding graph of T 2/R/4π 2 versus R2 ought yield a straight line such that the slope is g and the intercept is − 1 12L 2 . g = 9.7923 m/s 2 and L = 1.470 m Copyright c 2011 American Association of Physics Teachers

2011 Semifinal Exam Part A Question A3 A light bulb has a solid cylindrical filament of length L and radius a,and consumes power P. You are to design a new light bulb,using a cylindrical filament of the same material,operating at the same voltage,and emitting the same spectrum of light,which will consume power nP.What are the length and radius of the new filament?Assume that the temperature of the filament is approximately uniform across its cross-section;the filament doesn't emit light from the ends;and energy loss due to convection is minimal. Solution Since the new bulb emits the same spectrum of light,the emitted power is simply proportional to the area: P 2TaL P aL If the resistivity of the filament is p,the resistance is Ta2 and therefore the power is also given by p=y、V2ma2 五= pL a2 Combining our conditions, a x p2/3 L Pl/3 So the new filament must have length n2/3a and length n/3L. Question A4 In this problem we consider a simplified model of the electromagnetic radiation inside a cubical box of side length L.In this model,the electric field has spatial dependence E(x,y,z)=Eo sin(kzx)sin(kuy)sin(kzz) where one corner of the box lies at the origin and the box is aligned with the x,y,and z axes.Let h be Planck's constant,kB be Boltzmann's constant,and c be the speed of light. a.The electric field must be zero everywhere at the sides of the box.What condition does this impose on kz,ky,and k:?(Assume that any of these may be negative,and include cases where one or more of the ki is zero,even though this causes E to be zero.) b.In the model,each permitted value of the triple (ky,k)corresponds to a quantum state. These states can be visualized in a state space,which is a notional three-dimensional space Copyright C2011 American Association of Physics Teachers
2011 Semifinal Exam Part A 7 Question A3 A light bulb has a solid cylindrical filament of length L and radius a, and consumes power P. You are to design a new light bulb, using a cylindrical filament of the same material, operating at the same voltage, and emitting the same spectrum of light, which will consume power nP. What are the length and radius of the new filament? Assume that the temperature of the filament is approximately uniform across its cross-section; the filament doesn’t emit light from the ends; and energy loss due to convection is minimal. Solution Since the new bulb emits the same spectrum of light, the emitted power is simply proportional to the area: P ∝ 2πaL P ∝ aL If the resistivity of the filament is ρ, the resistance is R = ρL A = ρL πa2 and therefore the power is also given by P = V 2 R = V 2πa2 ρL P ∝ a 2 L Combining our conditions, a ∝ P 2/3 L ∝ P 1/3 So the new filament must have length n 2/3a and length n 1/3L. Question A4 In this problem we consider a simplified model of the electromagnetic radiation inside a cubical box of side length L. In this model, the electric field has spatial dependence E(x, y, z) = E0 sin(kxx) sin(kyy) sin(kzz) where one corner of the box lies at the origin and the box is aligned with the x, y, and z axes. Let h be Planck’s constant, kB be Boltzmann’s constant, and c be the speed of light. a. The electric field must be zero everywhere at the sides of the box. What condition does this impose on kx, ky, and kz? (Assume that any of these may be negative, and include cases where one or more of the ki is zero, even though this causes E to be zero.) b. In the model, each permitted value of the triple (kx, ky, kz) corresponds to a quantum state. These states can be visualized in a state space, which is a notional three-dimensional space Copyright c 2011 American Association of Physics Teachers