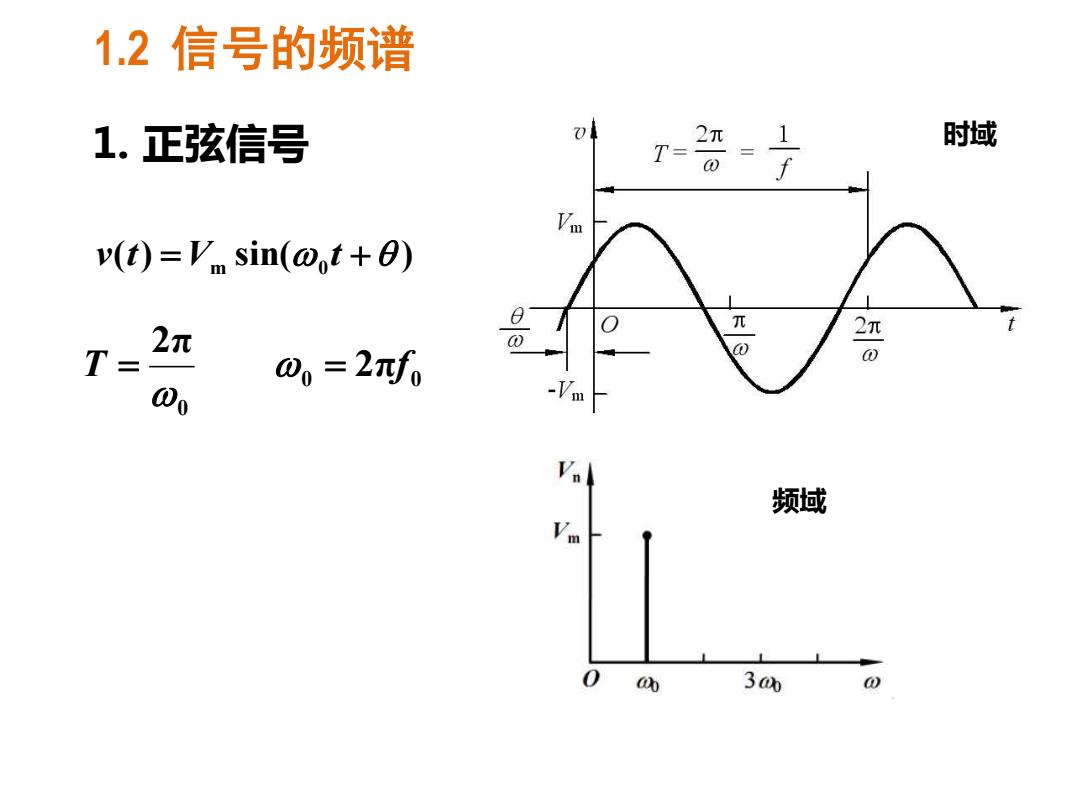
1.2信号的频谱 1.正弦信号 0 T= 2π1 时域 v(t)=V sin(@t+0) 2元 T= w=2f0 酒 00 -Vm 频域 0 a 3 0
1.2 信号的频谱 1. 正弦信号 ( ) sin( ) v t =Vm 0 t + 0 0 0 2π 2π T = = f 时域 频域

1.2信号的频谱 2π T= 2.方波信号 满足狄利克雷条件,展 开成傅里叶级数 方波的时域表示 ()= 2Vs(in+sin3sin5) 2 元 其中 2元 —基波角频率 Vs T 一一直流分量 2 2V基波分量 2V1 一三次谐波分量 元 π3
1.2 信号的频谱 2. 方波信号 sin5 ) 5 1 sin3 3 1 (sin π 2 2 ( ) 0 0 0 = S + S t + t + t + V V v t 满足狄利克雷条件,展 开成傅里叶级数 2 其中 VS ——直流分量 π 2VS ——基波分量 3 1 π 2 S V ——三次谐波分量 方波的时域表示 T 2π 0 = ——基波角频率

1.2信号的频谱 频谱:信号的振幅和相位随频率变化的分布称为该信号的频谱。 2.方波信号 +2 .(sinol+sin3o.t+sin50.+ 1 1 (t)= 2 元 3 傅里叶级数的标准形式 )= +2业2csna,t-2 2 元 =l,3,51 2V 300 500 2 2业 3元 2 5元 1 @6 3c 50 0 幅度谱 相位谱
1.2 信号的频谱 2. 方波信号 sin5 ) 5 1 sin3 3 1 (sin π 2 2 ( ) 0 0 0 = s + s t + t + t + V V v t 频谱:信号的振幅和相位随频率变化的分布称为该信号的频谱。 幅度谱 相位谱 傅里叶级数的标准形式 ) 2 π cos( 1 π 2 2 ( ) 1,3,5 0 s s = + − n= n t n V V v t
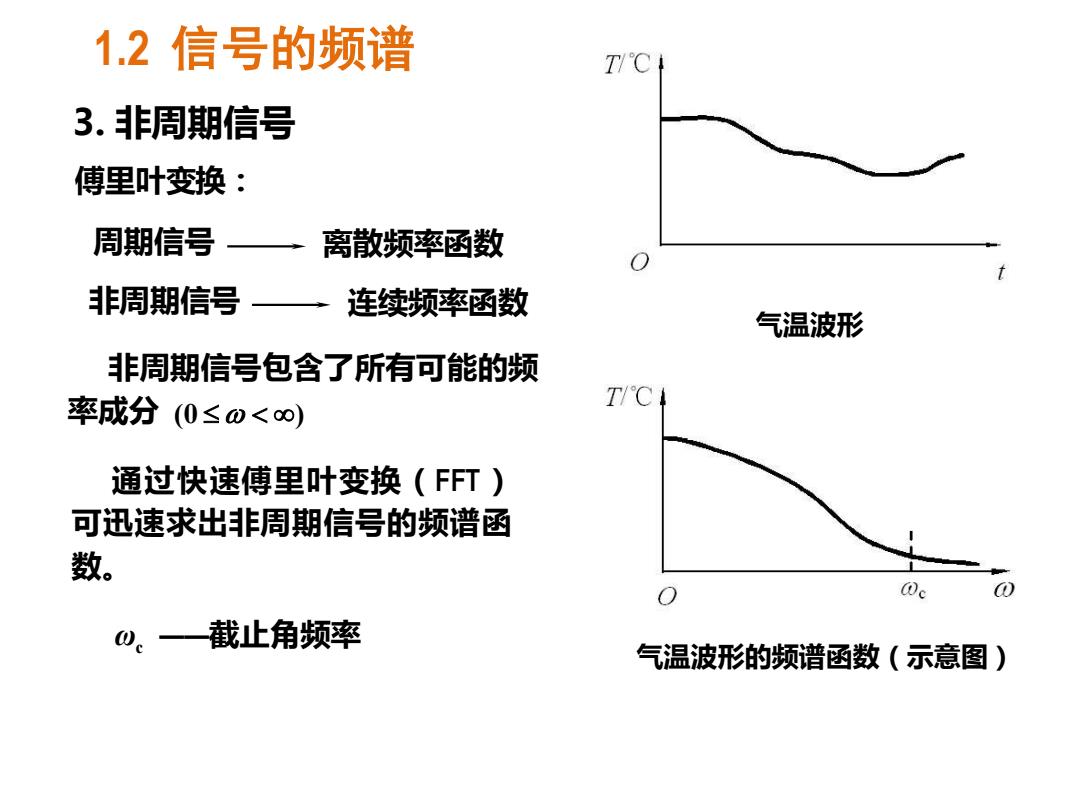
1.2信号的频谱 T℃ 3.非周期信号 傅里叶变换: 周期信号 离散频率函数 1 非周期信号一 连续频率函数 气温波形 非周期信号包含了所有可能的频 率成分(0≤0<∞) T/℃1 通过快速傅里叶变换(FFT) 可迅速求出非周期信号的频谱函 数。 ω。一—截止角频率 气温波形的频谱函数(示意图)
1.2 信号的频谱 3. 非周期信号 傅里叶变换: 通过快速傅里叶变换(FFT) 可迅速求出非周期信号的频谱函 数。 (0 ) 非周期信号包含了所有可能的频 率成分 周期信号 离散频率函数 非周期信号 连续频率函数 气温波形 气温波形的频谱函数(示意图) ωc ——截止角频率