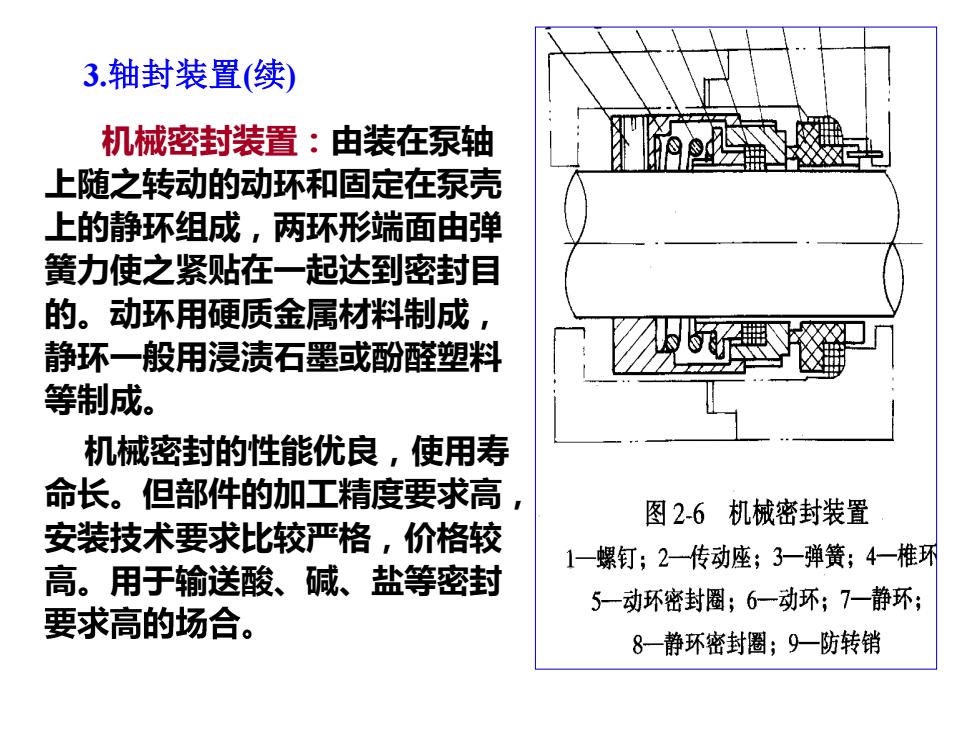
3.轴封装置(续) 机械密封装置:由装在泵轴 上随之转动的动环和固定在泵壳 上的静环组成,两环形端面由弹 簧力使之紧贴在一起达到密封目 的。动环用硬质金属材料制成 静环一般用浸渍石墨或酚醛塑料 等制成。 机械密封的性能优良,使用寿 命长。但部件的加工精度要求高, 图2-6机械密封装置 安装技术要求比较严格,价格较 1一螺钉;2一传动座;3一弹簧;4一椎环 高。用于输送酸、碱、盐等密封 5-动环密封圈;6一动环;7一静环; 要求高的场合。 8一静环密封圈;9一防转销
3.轴封装置(续) 机械密封装置:由装在泵轴 上随之转动的动环和固定在泵壳 上的静环组成,两环形端面由弹 簧力使之紧贴在一起达到密封目 的。动环用硬质金属材料制成, 静环一般用浸渍石墨或酚醛塑料 等制成。 机械密封的性能优良,使用寿 命长。但部件的加工精度要求高, 安装技术要求比较严格,价格较 高。用于输送酸、碱、盐等密封
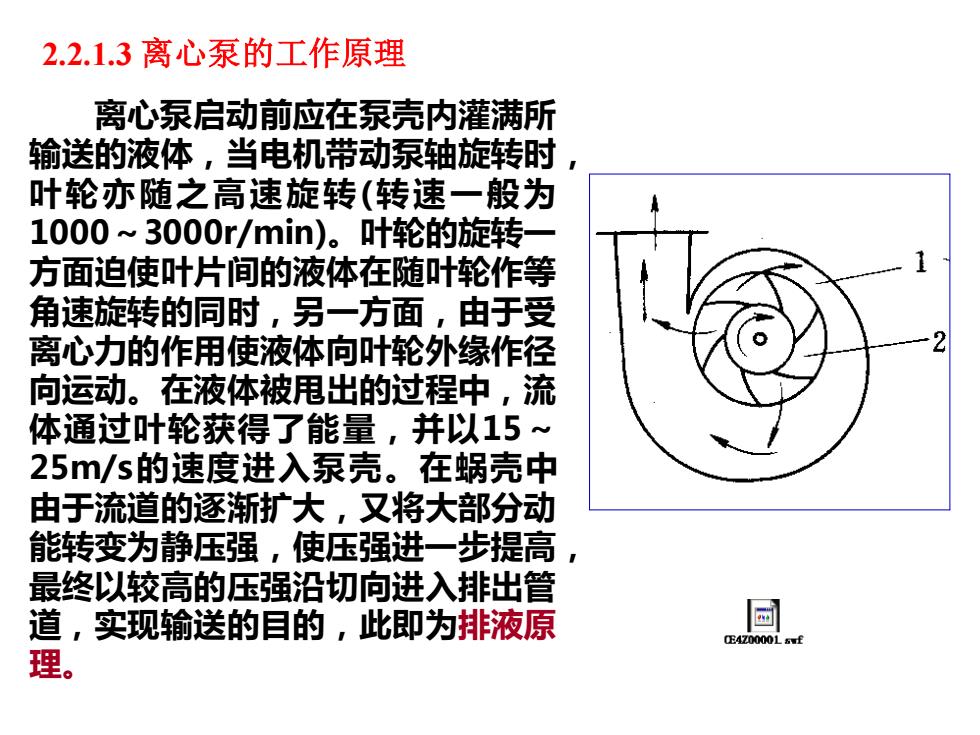
2.2.1.3离心泵的工作原理 离心泵启动前应在泵壳内灌满所 输送的液体,当电机带动泵轴旋转时 1 叶轮亦随之高速旋转(转速一般为 1000~3000r/min)。叶轮的旋转 方面迫使叶片间的液体在随叶轮作等 角速旋转的同时,另一方面,由于受 离心力的作用使液体向叶轮外缘作径 向运动。在液体被甩出的过程中,流 体通过叶轮获得了能量,并以15~ 25m/s的速度进入泵壳。在蜗壳中 由于流道的逐渐扩大,又将大部分动 能转变为静压强,使压强进一步提高, 最终以较高的压强沿切向进入排出管 道,实现输送的目的,此即为排液原 回 E4Z0000L5f 理
2.2.1.3 离心泵的工作原理 离心泵启动前应在泵壳内灌满所 输送的液体,当电机带动泵轴旋转时, 叶轮亦随之高速旋转(转速一般为 1000~3000r/min)。叶轮的旋转一 方面迫使叶片间的液体在随叶轮作等 角速旋转的同时,另一方面,由于受 离心力的作用使液体向叶轮外缘作径 向运动。在液体被甩出的过程中,流 体通过叶轮获得了能量,并以15~ 25m/s的速度进入泵壳。在蜗壳中 由于流道的逐渐扩大,又将大部分动 能转变为静压强,使压强进一步提高, 最终以较高的压强沿切向进入排出管 道,实现输送的目的,此即为排液原 理

当液体由叶轮中心流向外缘时,在叶 轮中心处形成了低压。在液面压强与泵内 压强差的作用下,液体经吸入管路进入泵 的叶轮内,以填补被排出液体的位置,此 即为吸液原理。只要叶轮旋转不停,液体 就被源源不断地吸入和排出,这就是离心 泵的工作原理。 若离心泵在启动前泵壳内不是充满液体而是空气,由于空气 的密度远小于液体的密度,产生的离心力很小,因而叶轮中心区 形成的低压不足以将贮槽内液体压入泵内,此时虽启动离心泵但 不能够输送液体,这种现象称作气缚。表示离心泵无自吸能力。 因此在启动泵前一定要使泵壳内充满液体。通常若吸入口位于贮 槽液面上方时,在吸入管路中安装一单向底阀和滤网,以防止停 泵时液体从泵内流出和吸入杂物
当液体由叶轮中心流向外缘时,在叶 轮中心处形成了低压。在液面压强与泵内 压强差的作用下,液体经吸入管路进入泵 的叶轮内,以填补被排出液体的位置,此 即为吸液原理。只要叶轮旋转不停,液体 就被源源不断地吸入和排出,这就是离心 泵的工作原理。 若离心泵在启动前泵壳内不是充满液体而是空气,由于空气 的密度远小于液体的密度,产生的离心力很小,因而叶轮中心区 形成的低压不足以将贮槽内液体压入泵内,此时虽启动离心泵但 不能够输送液体,这种现象称作气缚。表示离心泵无自吸能力。 因此在启动泵前一定要使泵壳内充满液体。通常若吸入口位于贮 槽液面上方时,在吸入管路中安装一单向底阀和滤网,以防止停 泵时液体从泵内流出和吸入杂物

2.2.2离心泵的基本方程式一一能量方程式 (一)问题的提出 离心泵的压头(即液体获得的静压能)与哪些因素有关?如何提高液体的 静压能? 离心泵的基本方程式是从理论上描述在理想情况下离心泵可能达到的最大 压头(扬程)与泵的结构、尺寸、转速及液体流量诸因素之间关系的表达式。由 于液体在叶轮中的运动情况十分复杂,很难提出一个定量表达上述各因素之 间关系的方程。工程上采用数字模型法来研究此类问题。 (二)数学模型的建立 1.简化假设 为了便于分析研究流体在叶轮内的运动情况,特作如下简化假设: (1)叶轮为具有无限薄、无限多叶片的理想叶轮,流体质点将完全沿着叶 片表面而流动,流体无旋涡、无冲击损失; (2)被输送的是理想液体,液体在叶轮内流动不存在流动阻力; (3)泵内为稳态流动过程。 按上面假想模型推导出来的压头必为在指定转速下可能达到的最大压头一 理论压头
2.2.2 离心泵的基本方程式――能量方程式 (一)问题的提出 离心泵的压头(即液体获得的静压能)与哪些因素有关?如何提高液体的 静压能? 离心泵的基本方程式是从理论上描述在理想情况下离心泵可能达到的最大 压头(扬程)与泵的结构、尺寸、转速及液体流量诸因素之间关系的表达式。由 于液体在叶轮中的运动情况十分复杂,很难提出一个定量表达上述各因素之 间关系的方程。工程上采用数字模型法来研究此类问题。 (二)数学模型的建立 1.简化假设 为了便于分析研究流体在叶轮内的运动情况,特作如下简化假设: (1) 叶轮为具有无限薄、无限多叶片的理想叶轮,流体质点将完全沿着叶 片表面而流动,流体无旋涡、无冲击损失; (2) 被输送的是理想液体,液体在叶轮内流动不存在流动阻力; (3) 泵内为稳态流动过程。 按上面假想模型推导出来的压头必为在指定转速下可能达到的最大压头— —理论压头

2.流体通过叶轮的流动一一速度三角形 理想流体在理想叶轮中的旋转运动应是等角速度的。 流体质点以绝对速度C0沿着轴向进入叶轮后,随即转化为径向运动,此时流 体一方面以圆周速度u1随叶轮旋转,其运动方向即流体质点所在位置的切线方向 而大小沿半径而变化;另一方面以相对速度W1在叶片间的径向作相对运动,其运 动方向是液体质点所在处叶片的切线方向,大小从里向外由于流道变大而降低。 二者的合速度为绝对速度c1,此即流体质点相对于泵壳的绝对速度。上述三个速 度W1、u1、C1所组成的矢量图称为速度三角形。同样,在叶轮出口处,圆周速度 u2、相对速度W2及绝对速度c2也构成速度三角形。c表示绝对速度与圆周速度两 矢量之间的夹角,表示相对速度与圆周速度反方向延线的夹角,称之为流动角。 c及β的大小与叶片的形状有关。 切2 (a) (0): (a)后弯叶片(b)径向叶片(c)前弯叶片 图2-7叶片形状及出口速度三角形
2.流体通过叶轮的流动――速度三角形 理想流体在理想叶轮中的旋转运动应是等角速度的。 流体质点以绝对速度c0沿着轴向进入叶轮后,随即转化为径向运动,此时流 体一方面以圆周速度u1随叶轮旋转,其运动方向即流体质点所在位置的切线方向, 而大小沿半径而变化;另一方面以相对速度w1在叶片间的径向作相对运动,其运 动方向是液体质点所在处叶片的切线方向,大小从里向外由于流道变大而降低。 二者的合速度为绝对速度c1,此即流体质点相对于泵壳的绝对速度。上述三个速 度w1、u1、c1所组成的矢量图称为速度三角形。同样,在叶轮出口处,圆周速度 u2、相对速度w2及绝对速度c2也构成速度三角形。α表示绝对速度与圆周速度两 矢量之间的夹角,β表示相对速度与圆周速度反方向延线的夹角,称之为流动角。 α及β的大小与叶片的形状有关