
5.2图像噪声的空间和频率特性 数字图像的噪声主要来源于图像的获取(数字化 过程)和传输过程。 ·噪声的空间和频率特性: 一频率特性:噪声在傅里叶变换域的频率特性。 空间特性:噪声与空间坐标的关系。 (除周期噪声以外,本章中假设噪声独立于空间坐标, 并且它与图像内容无关联) 空间噪声利用退化模型中噪声分量的灰度值统计 特性来表示,可以被认为是由概率密度函数 (PDF)表示的随机变量
5.2 图像噪声的空间和频率特性 • 数字图像的噪声主要来源于图像的获取(数字化 过程)和传输过程。 • 噪声的空间和频率特性: – 频率特性:噪声在傅里叶变换域的频率特性。 – 空间特性:噪声与空间坐标的关系。 (除周期噪声以外,本章中假设噪声独立于空间坐标, 并且它与图像内容无关联) • 空间噪声利用退化模型中噪声分量的灰度值统计 特性来表示,可以被认为是由概率密度函数 (PDF)表示的随机变量
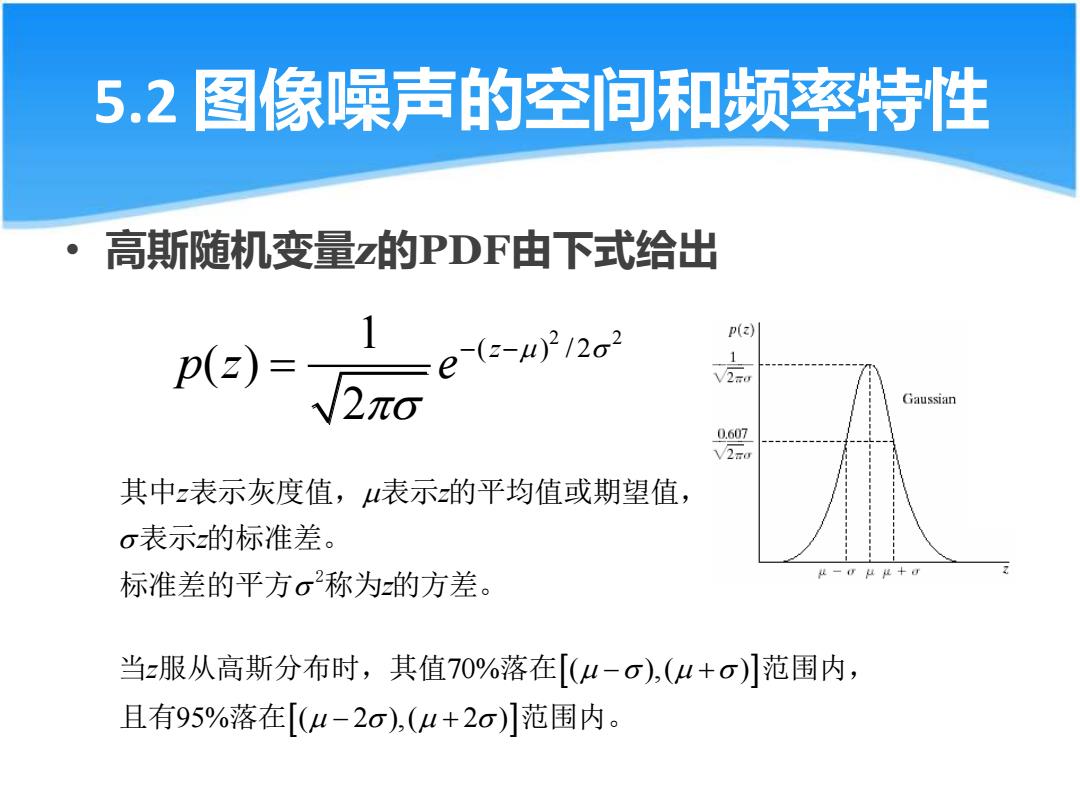
5.2图像噪声的空间和频率特性 高斯随机变量z的PDF由下式给出 a) p(z) Gaussian 0.607 V2云d 其中z表示灰度值,表示的平均值或期望值, o表示的标准差。 标准差的平方σ称为的方差。 当z服从高斯分布时,其值70%落在[(4-o),(u+o)]范围内, 且有95%落在[(u-2o),(u+2o)]范围内
5.2 图像噪声的空间和频率特性 • 高斯随机变量z的PDF由下式给出 2 2 1 ( ) / 2 ( ) 2 z p z e − − = z z z z 2 其中 表示灰度值, 表示 的平均值或期望值, 表示 的标准差。 标准差的平方 称为 的方差。 70% ( ),( ) 95% ( 2 ),( 2 ) z − + − + 当 服从高斯分布时,其值 落在 范围内, 且有 落在 范围内

5.2 图像噪声的空间和频率特性 瑞利噪声的PDF由下式给出 Pl)(e 0 z≥a 0.5 0.4 0 z <a 0.3 0.2 概率密度的均值和方差由下式给定: 0.1 4 u=a+Vπb/4 123 b(4-π) 4 瑞利密度对于近似偏移的直方图十分适用。 当一个随机二维向量的两个分量呈独立的、有着相同的方差的正态分布时,这个向量的 模呈瑞利分布
5.2 图像噪声的空间和频率特性 • 瑞利噪声的PDF由下式给出 • 瑞利密度对于近似偏移的直方图十分适用。 2 2 ( ) / ( ) ( ) 0 z a b z a e z a p z b z a − − − = 当一个随机二维向量的两个分量呈独立的、有着相同的方差的正态分布时,这个向量的 模呈瑞利分布 : a b / 4 = + 2 概率密度的均值和方差由下式给定 b(4- ) = 4
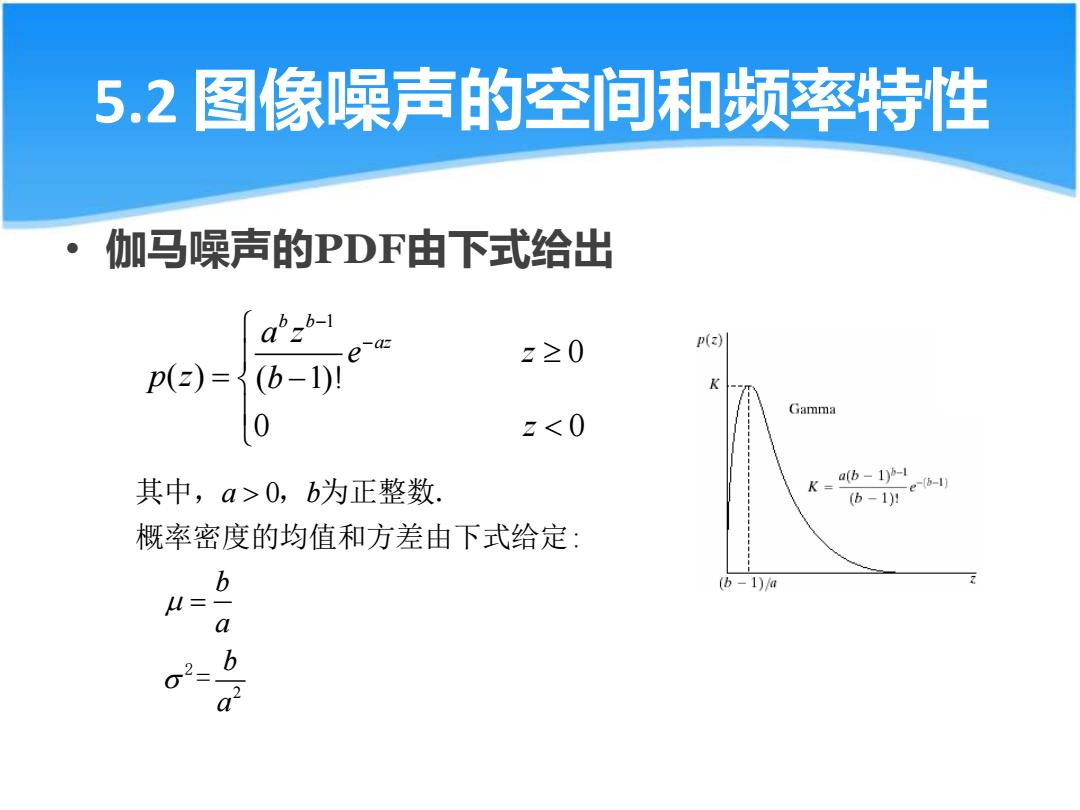
5.2 图像噪声的空间和频率特性 伽马噪声的PDF由下式给出 aPzb e a z≥0 p(z) p(z)=(b-1)! Gamma 0 z<0 其中,a>0,b为正整数, ab-1)- e-6-l (b-1)1 概率密度的均值和方差由下式给定: b (b-1)/a a b 2
5.2 图像噪声的空间和频率特性 • 伽马噪声的PDF由下式给出 1 0 ( ) ( 1)! 0 0 b b a z az e z p z b z − − = − 2 0 : a b b a b a = 2 其中, , 为正整数. 概率密度的均值和方差由下式给定 =
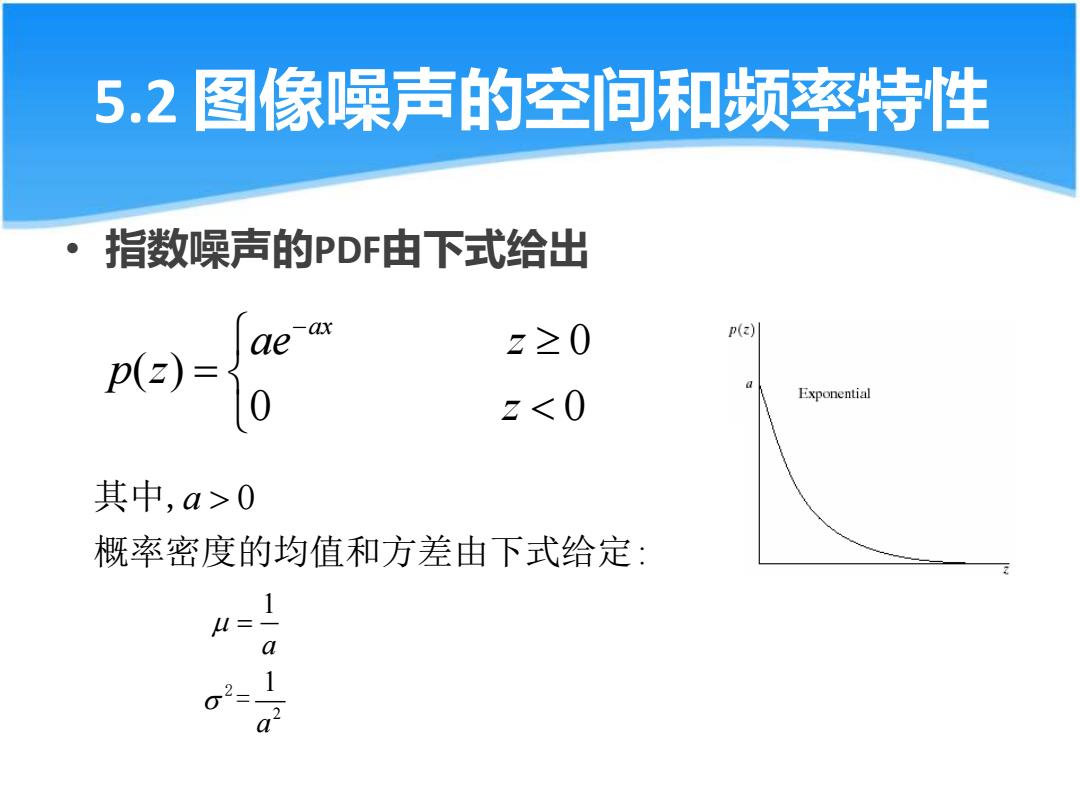
5.2 图像噪声的空间和频率特性 指数噪声的PDF由下式给出 z≥0 p(z) p(z)= 0 z<0 Exponential 其中,a>0 概率密度的均值和方差由下式给定: 1 a 1
5.2 图像噪声的空间和频率特性 • 指数噪声的PDF由下式给出 2 1 1 a a = 2 = 0 ( ) 0 0 ax ae z p z z − = 0 : 其中,a 概率密度的均值和方差由下式给定