
热力学第一章 20、反应热与温度的关系 AH(G)-AI(T)+Cd R(T,P) △,Hm(T) PT,p) △.Hm(T)=△H1+△Hm+△Hm C(RT+,H()+c(PT R(T2 PA P(Ta,P) =4,H.()+aAC,nd7 注意:T1~T2间任何物质不能发生相变 如在该温度区间内有物质发生相变,就要分段积分
20、反应热与温度的关系 H T H T C T T T ( ) ( ) p d 2 1 r m 2 = r m 1 + r ,m R(T1 , p) P(T1 , p) rHm(T1 ) R(T2 , p) P(T2 , p) rHm(T2 )=? Ⅰ Ⅱ Ⅲ r Hm (T2 ) = HⅠ+ HⅡ + HⅢ = + + 2 1 1 2 ,m (R)d r m ( 1 ) ,m (P)d T T p T T Cp T H T C T = + 2 1 r m ( 1 ) r ,m d T T H T Cp T 注意:T1~T2间任何物质不能发生相变 如在该温度区间内有物质发生相变,就要分段积分。 热力学第一章

热力学第一章 21、理想气体简单状态变化过程 AU-CT-nCd △l=jhC,dr=jn-Cndn w-fnav- -P(V-V)(等外压) 0 (恒容) AU=∫C, ”(绝热) O=△UJ-W (定温可逆)
21、理想气体简单状态变化过程 2 2 1 1 , T T V V m T T = = U C dT n C dT 2 2 1 1 , T T p p m T T = = H C dT n C dT W p dV = − = e 2 1 ( ) e − − p V V (等外压) 0 (恒容) U (绝热) 2 1 T V T = C dT Q = − U W 2 1 lnV pdV nRT V − = − (定温可逆) 热力学第一章

热力学第一章 22、相变化过程 可逆相变 △H=n·△相Hm △U=Q+W=△H-p△V w=-∫p.aW=-∫pW=-p-) =-pV =-nRT (末态为气态,且 为理想气体) =AH 不可逆相变 △U和△H可通过在始终态间设计过程计 算,W和Q必须按照实际途径计算
22、相变化过程 可逆相变 = H n H相 m W e = − = − p dV pdV 2 1 = − − p V V ( ) g = − = − pV nRT (末态为气态,且 为理想气体) = + U Q W = − H p V Q H p = 不可逆相变 ΔU和ΔH可通过在始终态间设计过程计 算,W和Q必须按照实际途径计算 热力学第一章

热力学第一章 23、化学变化过程 AH=5△,H=5(∑yA,H)=(-∑yBAH) △U=5·△,UA=5A,HR-∑yRT) w (定压) (定容) O=△H (定压,W'=0) Q=△U (定容,W=0)
23、化学变化过程 r m H H = ( ) B f m H = ( ) B c m H = − U Ur m = ( ) r m g H RT = − W p dV = − e ( ) g = − = − p V n RT (定压) = 0 (定容) Q H = (定压, W’=0) Q = U (定容, W’=0) 热力学第一章
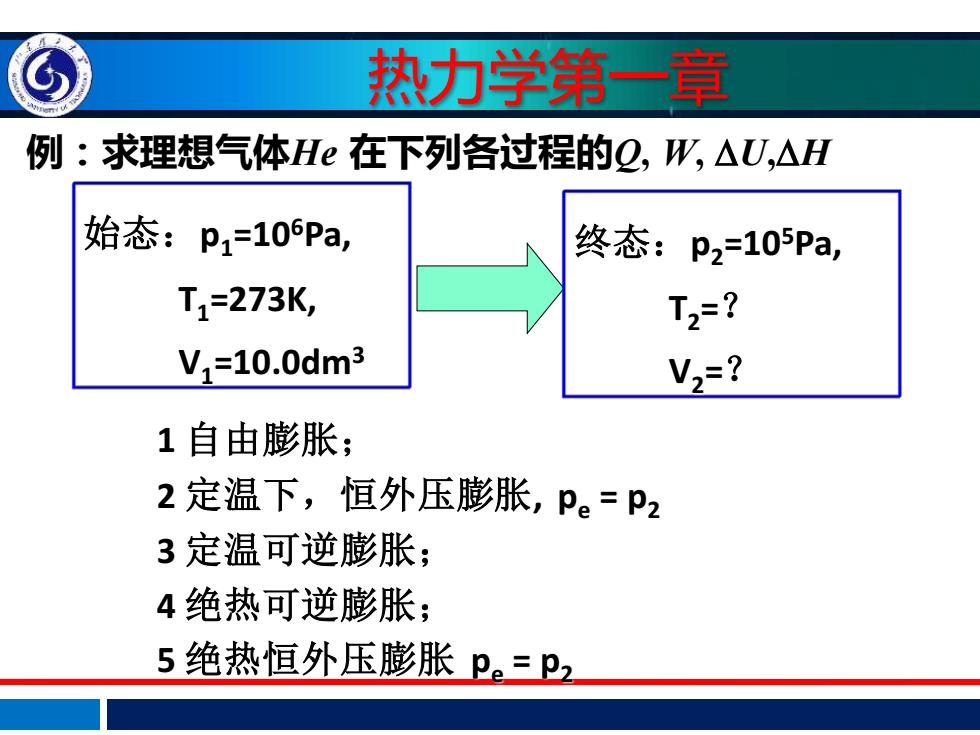
热力学第一章 例:求理想气体H在下列各过程的2,W,△U,△H 始态:p1=10Pa, 终态: p2=105Pa, T1=273K, T2=? V,=10.0dm3 V2=? 1自由膨胀; 2定温下,恒外压膨胀,P。=P2 3定温可逆膨胀; 4绝热可逆膨胀; 5绝热恒外压膨胀p。=p2
例:求理想气体He 在下列各过程的Q, W, U,H 1 自由膨胀; 2 定温下,恒外压膨胀, pe = p2 3 定温可逆膨胀; 4 绝热可逆膨胀; 5 绝热恒外压膨胀 pe = p2 始态:p1 =106Pa, T1 =273K, V1 =10.0dm3 终态:p2 =105Pa, T2 =? V2 =? 热力学第一章