
偏摩尔量的定义 在多组分系统中,每个热力学函数的变量就 不止两个,还与组成系统各物的物质的量有关 设系统中有1,2,3,·,k个组分 系统中任一容量性质Z(代表V,U,H,S, A,G等)除了与温度、压力有关外,还与各 组分的数量有关,即 Z=Z(T,p,n,n,...,n) 如果温度、压力和组成有微小的变化,则 系统中任一容量性质Z的变化为:
偏摩尔量的定义 在多组分系统中,每个热力学函数的变量就 不止两个,还与组成系统各物的物质的量有关 1 2 k Z Z T p n n n = ( , , , , , ) 系统中任一容量性质Z(代表V,U,H,S, A,G等)除了与温度、压力有关外,还与各 组分的数量有关,即 设系统中有 1,2,3, ,k 个组分 如果温度、压力和组成有微小的变化,则 系统中任一容量性质Z的变化为:
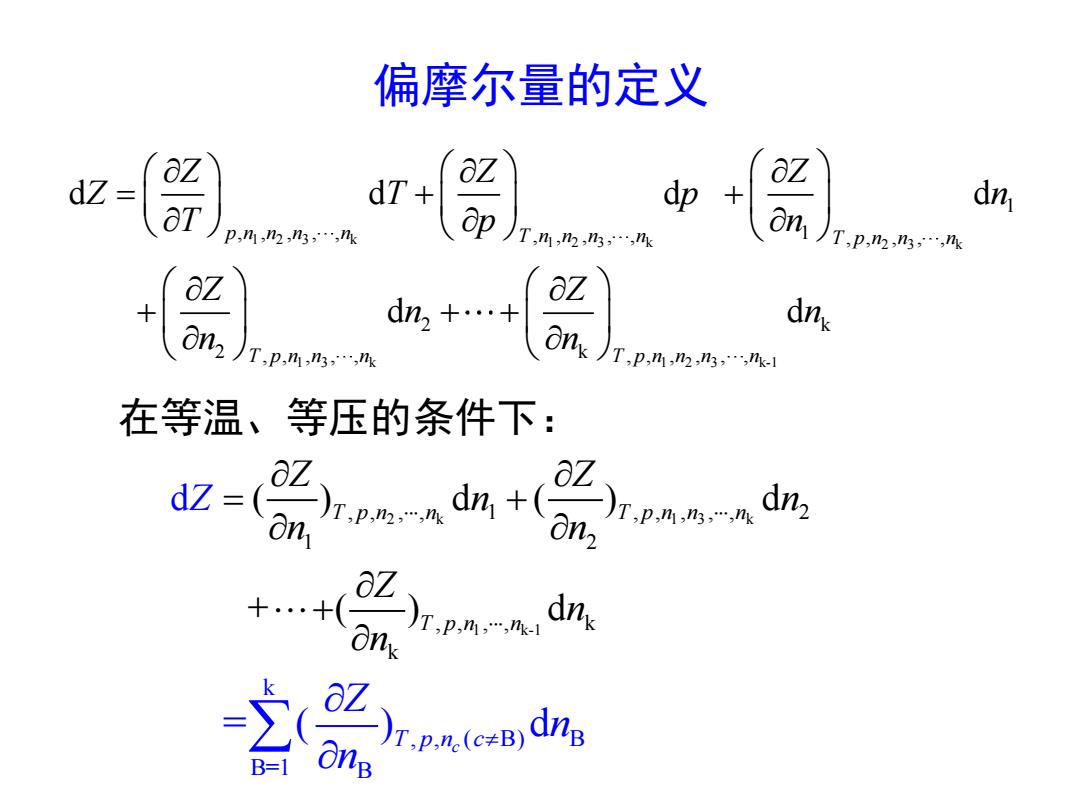
偏摩尔量的定义 dZ dT+ aZ OZ dp + O dn P,1,n2,n3,…,hk ap T,n,h,乃… 1T,p,n2n3…m aZ aZ On dnx 2T,p,3…m On)T.pA,两m 在等温、等压的条件下: d=货咖朗-品nd 品an B-
偏摩尔量的定义 1 2 3 k 1 2 3 k 2 3 k 1 3 k 1 2 3 k-1 1 , , , , , , , , , , 1 , , , , , 2 k 2 k , , , , , , , , , , , d d d d d d p n n n n T n n n n T p n n n T p n n n T p n n n n Z Z Z Z T p n T p n Z Z n n n n = + + + + + 在等温、等压的条件下: 2 k 1 3 k 1 k-1 , , , , 1 , , , , , 2 1 2 , , , , k k d ( ) d ( ) d + ( ) d T p n n T p n n n T p n n Z Z n n n n Z n n Z = + + k , , ( B) B B=1 B = ( ) d T p n c c Z n n

偏摩尔量的定义 偏摩尔量Z的定义为: Ze def OZ n ).n.(cB Z3称为物质B的某种容量性质Z的偏摩尔量 代入下式并整理得 d-交0aw B=1 =Z,dn1+Z2dn2+…+Zdnk =∑Zdne B=1
偏摩尔量的定义 B , , (c B) B def ( )T p nc Z Z n 偏摩尔量ZB的定义为: ZB称为物质B的某种容量性质Z的偏摩尔量 代入下式并整理得 k , , ( B) B B=1 B d ( ) d T p n c c Z Z n n = = + ++ Z n Z n Z n 1 1 2 2 k k d d d k B B B=1 = Z nd
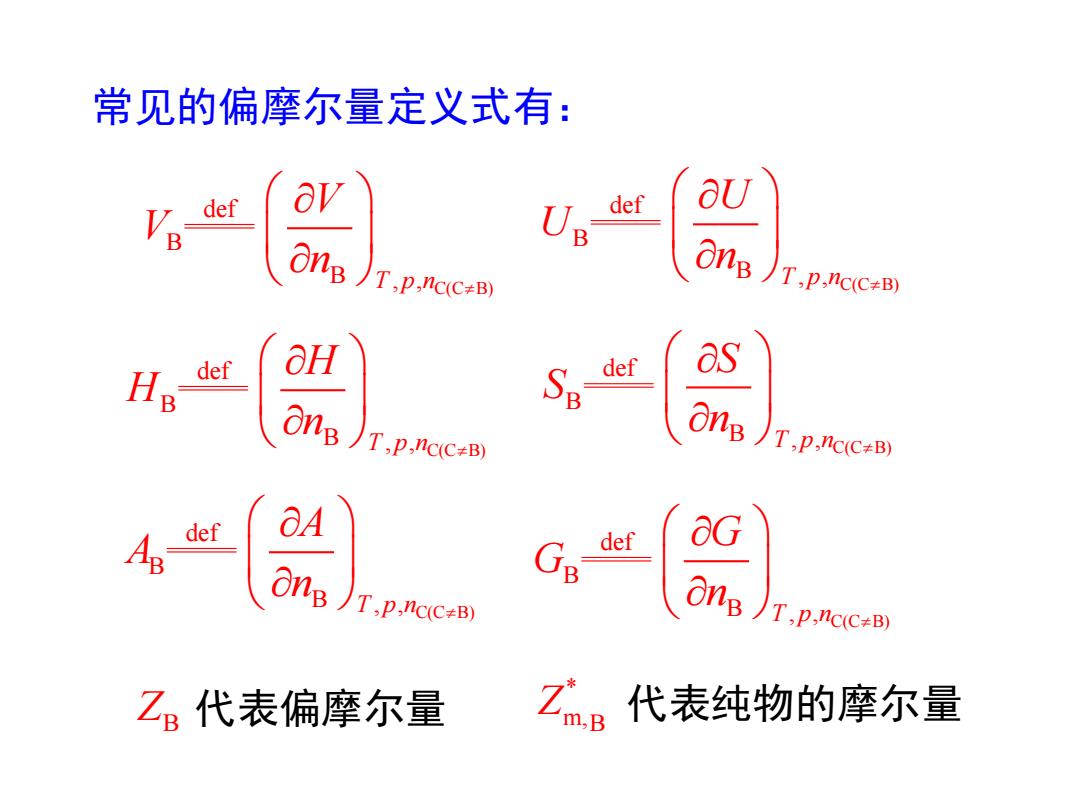
常见的偏摩尔量定义式有: def av def aU ong )T.p.ncc-) ong )T.p.ncc+B) Hg ef aH def as ong )T.p.ncc-B) On B T,p.nc(C+B) def OA def OG ong )T.p.ncc-) ong )T.p.ncc-) Z代表偏摩尔量 Zm.B 代表纯物的摩尔量
常见的偏摩尔量定义式有: C(C B) B B , , def T p n V V n C(C B) B B , , def T p n U U n C(C B) B B , , def T p n H H n C(C B) B B , , def T p n S S n C(C B) B B , , def T p n A A n C(C B) B B , , def T p n G G n ZB 代表偏摩尔量 代表纯物的摩尔量 * m,B Z

意义: ①指定T、D条件下,在各组分浓度确定的大量 系统中,加入1molB组分所引起系统容量性质的改 变. ②指定T、条件下,在有限量系统中,其它组 分不变(nc不变)的条件下,加入无限小量dnB摩尔 的B组分所引起系统容量性质的改变 核心:都是保持系统浓度不变
② 指定T、p条件下, 在有限量系统中, 其它组 分不变 (nC不变)的条件下, 加入无限小量 dnB 摩尔 的 B 组分所引起系统容量性质的改变. 意义: ① 指定T、p条件下, 在各组分浓度确定的大量 系统中, 加入 1mol B组分所引起系统容量性质的改 变. 核心:都是保持系统浓度不变