
第四章 流体混合物的热力学性质
第四章 流体混合物的热力学性质

·4.1变组分体系热力学性质间的关系 "4.2化学位和偏摩尔性质 ·4.3混合物的逸度与逸度系数 ·4.4理想溶液和标准态 4.5活度与活度系数 4.6混合过程性质变化 4.7超额性质 4.8活度系数与组成的关联 4.9习题计算
▪ 4.1 变组分体系热力学性质间的关系 ▪ 4.2 化学位和偏摩尔性质 ▪ 4.3 混合物的逸度与逸度系数 ▪ 4.4 理想溶液和标准态 ▪ 4.5 活度与活度系数 ▪ 4.6 混合过程性质变化 ▪ 4.7 超额性质 ▪ 4.8 活度系数与组成的关联 ▪ 4.9 习题计算

4.1 变组成体系热力学性质 之间的关系式 ·对于单相,纯物质组成体系,热力学性质间的关系式: 对1mo1 H=U+PV A U-TS G=H-TS U+PV-TS n mol nH=nU+n(PV) nA=nU-T(nS) nG=nH-T(nS)=nU+P(nV)-T(nS)
4.1 变组成体系热力学性质 之间的关系式 ▪ 对于单相,纯物质组成体系,热力学性质间的关系式: 对1mol H = U+PV A = U-TS G = H-TS = U+PV-TS n mol nH= nU+ n(PV) nA= nU-T(nS) nG= nH-T(nS)= nU+P(nV)-T(nS)
对应微分方程 对1mo1 对nmol ·dU=TdS-PdV -dU,=d (nU)=Td(nS)-Pd(nV) dH=TdS+VdP dH,=d (nH)=Td(nS)+(nV)dP dA=-SdT-PdV dA:=d (nA)=-(nS)dT-Pd (nV) dG=-SdT+VdP dG:=d (nG)=-(nS)dT+(nV)dP Maxwe I I:关系式对此也适用
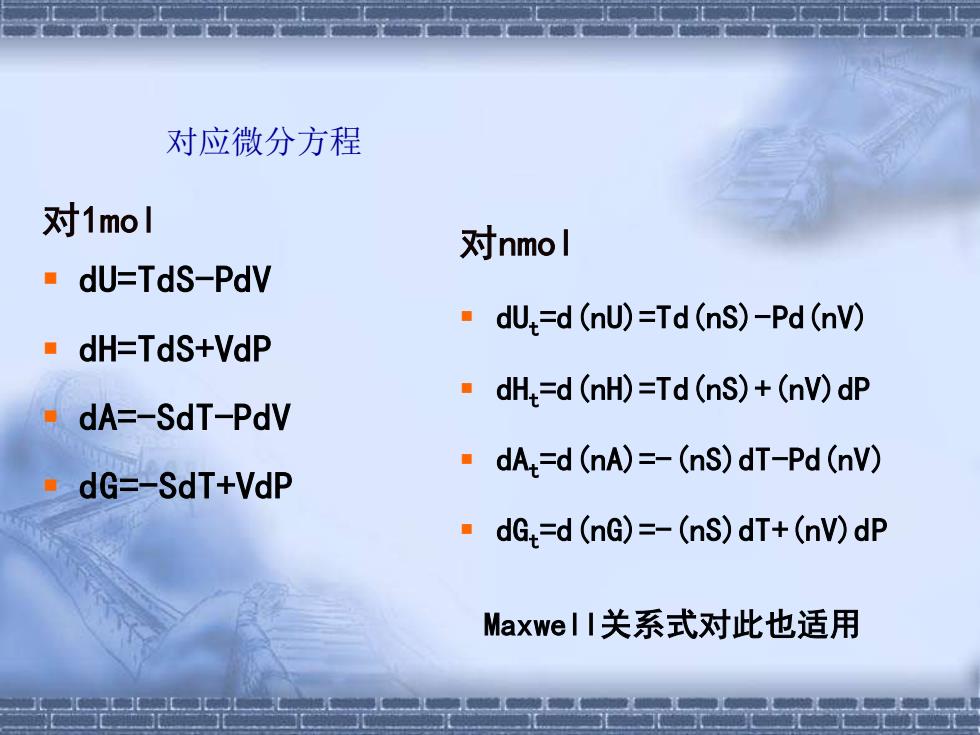
对应微分方程 对1mol ▪ dU=TdS-PdV ▪ dH=TdS+VdP ▪ dA=-SdT-PdV ▪ dG=-SdT+VdP 对nmol ▪ dUt=d(nU)=Td(nS)-Pd(nV) ▪ dHt=d(nH)=Td(nS)+(nV)dP ▪ dAt=d(nA)=-(nS)dT-Pd(nV) ▪ dGt=d(nG)=-(nS)dT+(nV)dP Maxwell关系式对此也适用

对于可变组成的单相体系: U-nU=f(nS,nV,n1,n2,.,n,.) 式中n:是i组份的摩尔数 内能的全微分式为: ai (n) sany2dh+ )-
对于可变组成的单相体系: Ut =nU=f(nS,nV,n1 ,n2 ,.,ni ,.) 式中ni是i组份的摩尔数 内能的全微分式为: dUt=d(nU)= d(nS) nS nU nV ,n ] ( ) ( ) [ , 1, 1 1 , ] ( ) ] ( ) [ ( ) ( ) [ + + n j n S n n S n V dn n nU d nV nV nU + + , , 2 2 2 ] ( ) [ dn n nU jj nS nV n ] ( ) ( ) ( ) ] ( ) [ ( ) ( ) [ , , d nV nV nU d nS nS nU nV n nS n + = nS nV n i i dn n nU + , , ] ( ) [