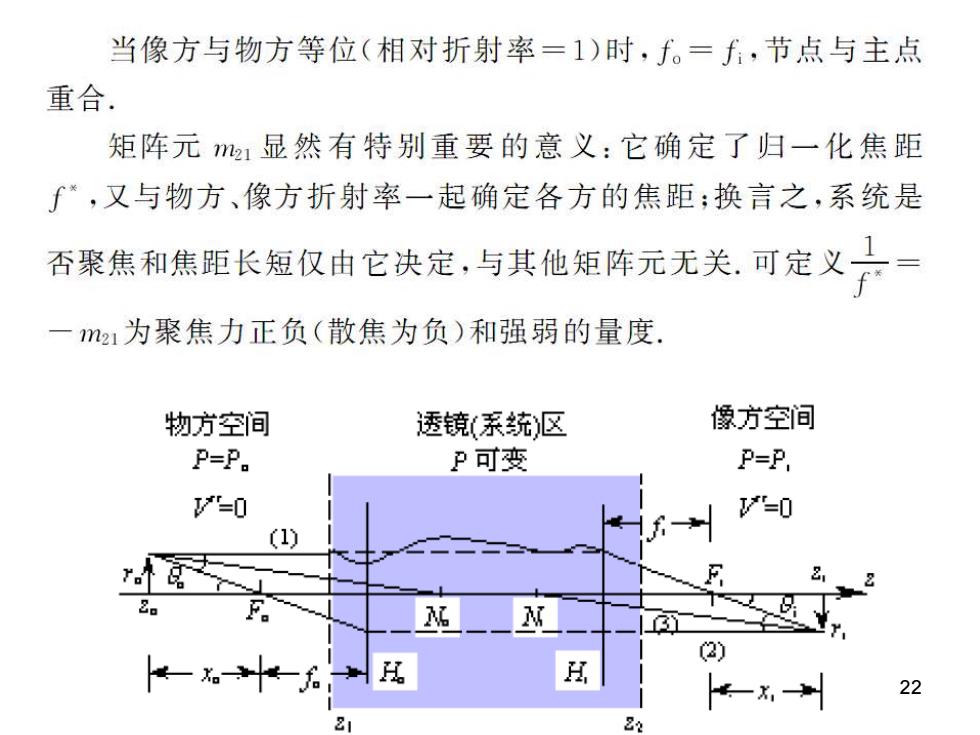
当像方与物方等位(相对折射率=1)时,f。=f,节点与主点 重合. 矩阵元21显然有特别重要的意义:它确定了归一化焦距 ∫,又与物方、像方折射率一起确定各方的焦距;换言之,系统是 否聚焦和焦距长短仅由它决定,与其他矩阵元无关.可定义子 21为聚焦力正负(散焦为负)和强弱的量度. 物方空间 透镜(系统)区 像方空间 P=P. P可变 P=P, "=0 =0 (1) F 2) 以 22 2
22

在得到上述公式的同时,已证明了几何光学中若干个著名的 定理,如: 物方,像方焦距之比等于两方空间的相对折射率,即。=卫 P 牛顿公式:x·x=f。·f 高斯公式:专十专-1当=时,为点十专=方。=月 拉格朗日公式:M,·M,· 1 P。 这些定理的发现者都曾显赫一时,可以想见这些定理对几何 光学的发展曾起过重要作用.它们对解决电子光学中的高斯轨迹 问题同样有效,在有关电子光学的计算中应能灵活运用这些定理」 例如,已知透镜系统的基点和物距,可由M,=1。、求得单向放 1 o 大率,再用高斯公式求像距. fo 23
23

只要高斯勄迹方程成立.传输矩阵尸得到.诱镜系统的基点很 M, 0 容易 一 步假过 M, 0 生代替 透镜 M 使用下ūM 1 (以别 于后义延判时逊以估足件省代法同本, f 第一种矩阵替代法为直接使用物点到像点的成像矩阵.如“光 路系统”中多次、接续成像,显然此法艰方便.因为每次成像的“物” 即为上次的“像”(无论实、虚),矩阵可直接在乘.易知此时总的单 向放大率、角放大率即等于各次放大率的连乘积,最终像的位置亦 可从计算中得到;但轨迹的细节不得防知.此种矩阵是 有人用几何相空间处理此问题状态用r和的列向量表示, 则当像点、物点不等位,即P≠办。时,应将物理相空间传输矩阵 的第2列乘以P。、第2行除以P而得到几何相空间传输矩阵(其 行列式值等于是,正反映才几何相空间父射度的变化).这种几何 相空间的成像矩阵是
24

第二种替代法是将透镜系统等效于两个“延伸漂移段”夹一薄 透镜,如同前述.此法与几何作图法等效.薄透镜的唯一异于单位 矩阵的矩阵元21与全系统原来的传输矩阵一样.即 M=M·M·Mo 1 2—之HH 之Ho一 P P。 0 1 22-1 21 此式是严格成立的.使用此法时,勿忘将薄透镜两侧看作与物 方、像方空间同折射率的等位区(假设“充以媒质”):且当两方折射 率不等时,两侧焦距不同.两侧无等位区而是加速区时,处理上麻 烦一些.此法当然也得不到透镜区内部的真实轨迹
25

行文至此,似应就由薄透镜和漂移段组成的系统稍加说明.这 不仅因为刚才提到了“精确的”薄透镜替代法,下文就要谈到“薄透 镜近似法”,而且因为与薄透镜有关的矩阵乘法可通过手算(无须 计算机)进行,是束流光学计算的基本功. 前已述及,薄透镜和漂移段对应的矩阵是两种最简单的传输 矩阵,它们与单位矩阵的区别分别只有一个矩阵元:前者是21= 子(此处暂不区别f和归一化焦矩∫“),后者则是m:= (可 称为等效长度).容易看出,如将两个紧密相连的薄透镜矩阵链接, 只需将其21项相加:而几个漂移段矩阵链接,也只需将其等效长 度相加.所以,如能用“漂移段十薄透镜十漂移段”(精确地或近似 地)替代一个透镜系统,而该系统两侧的空间原确为漂移段,只要 把它们各延长一个已知长度,不必增加矩阵个数,即可把透镜皆变 为薄透镜
26