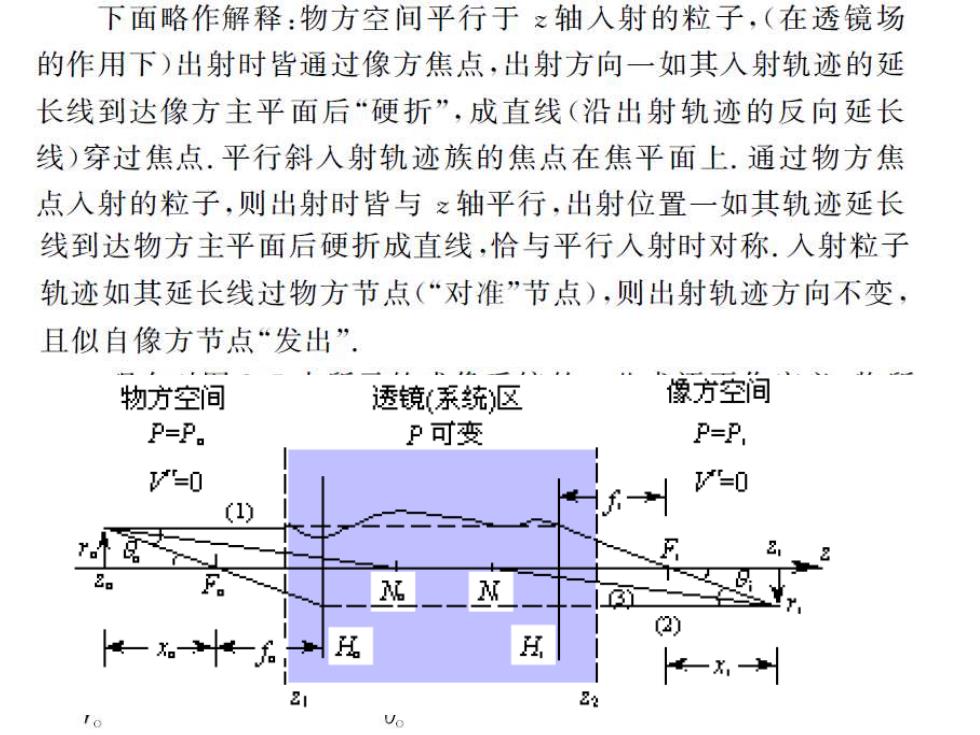
下面略作解释:物方空间平行于之轴人射的粒子,(在透镜场 的作用下)出射时皆通过像方焦点,出射方向一如其入射轨迹的延 长线到达像方主平面后“硬折”,成直线(沿出射轨迹的反向延长 线)穿过焦点.平行斜入射轨迹族的焦点在焦平面上.通过物方焦 点入射的粒子,则出射时皆与之轴平行,出射位置一如其轨迹延长 线到达物方主平面后硬折成直线,恰与平行入射时对称.入射粒子 轨迹如其延长线过物方节点(“对准”节点),则出射轨迹方向不变, 且似自像方节点“发出” 物方空间 透镜(系统)区 像方空间 P=P。 P可变 P=P. "=0 =0 (1) F F 】 2) 21 22 Vo
17
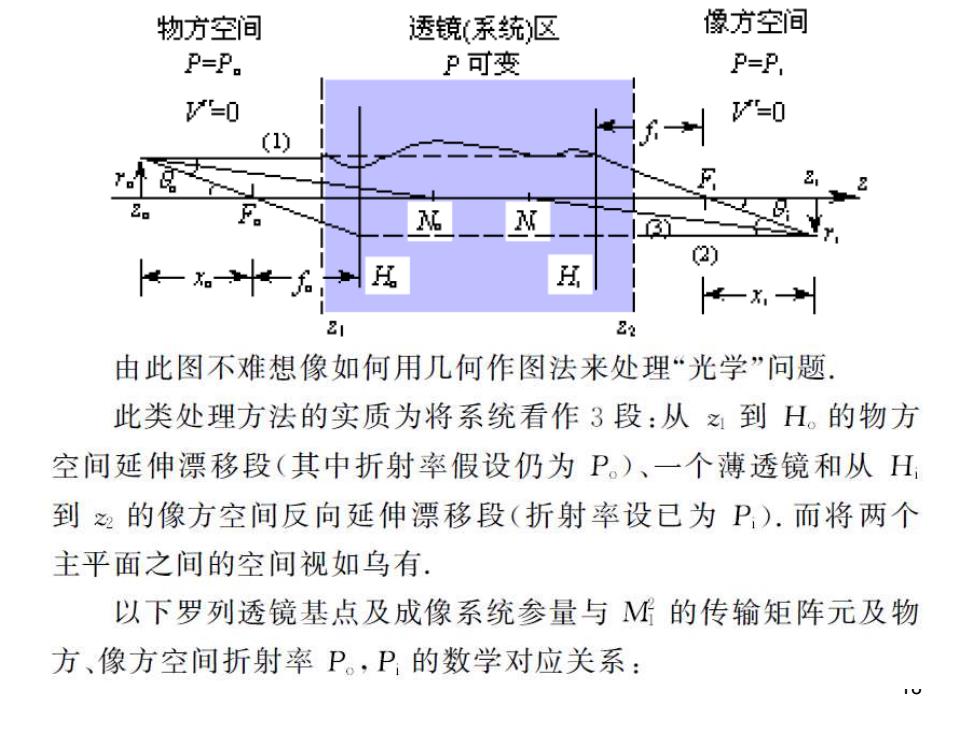
物方空间 透镜(系统)区 像方空间 P=P. P可变 P=P. "=0 "=0 (1) F 2 2 2) 。6 21 22 由此图不难想像如何用几何作图法来处理“光学”问题, 此类处理方法的实质为将系统看作3段:从之到H。的物方 空间延伸漂移段(其中折射率假设仍为P。)、一个薄透镜和从H 到忽的像方空间反向延伸漂移段(折射率设已为P).而将两个 主平面之间的空间视如乌有. 以下罗列透镜基点及成像系统参量与M的传输矩阵元及物 方、像方空间折射率P。,P的数学对应关系: IU
18
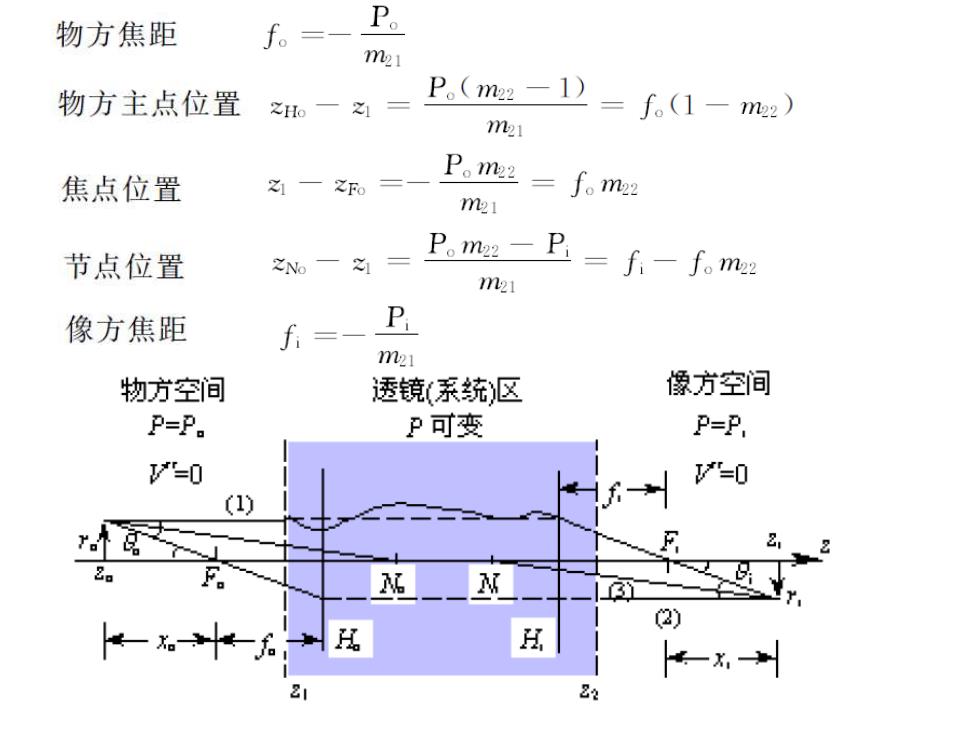
物方焦距 f。= P。 m21 物方主点位置 P。(m22-1) ZHo f。(1-m2) m21 焦点位置 P。m2=∫。m22 m2i 节点位置 P。m22- 之%一 21 卫=f-f。m 像方焦距 P m21 物方空间 透镜(系统)区 像方空间 P=P. P可变 P=P, =0 "=0 (1) 8 2 F 2) 22
19
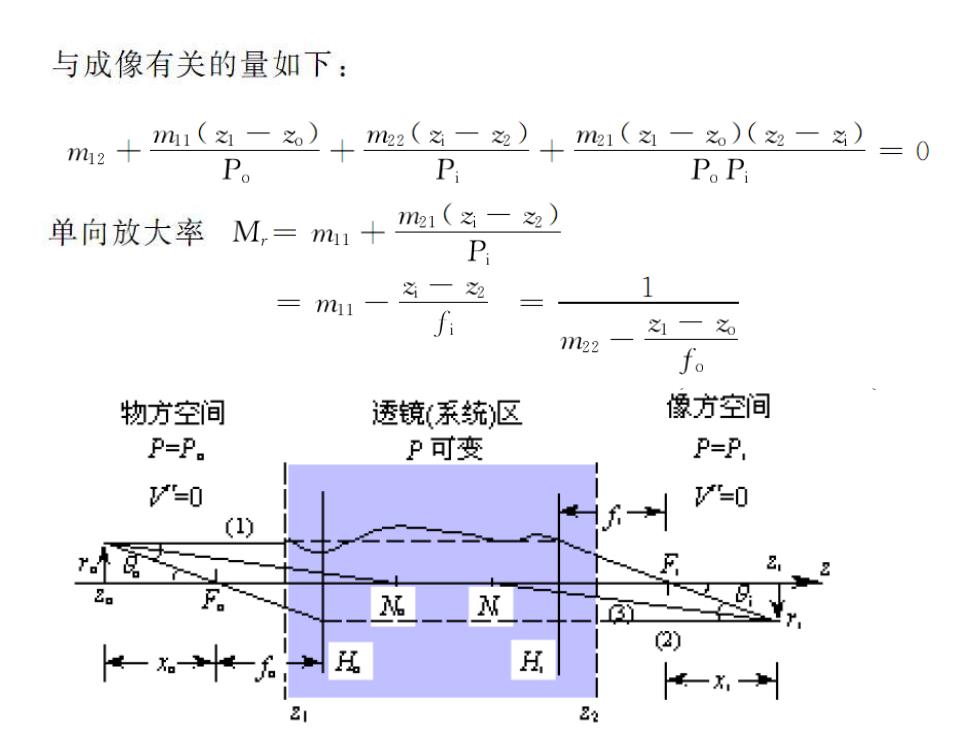
与成像有关的量如下: m:十m(-之)+:(名-)+他1(名-)(一) P。 P P。P 二0 单向放大率M,=m1十1(一之) P 必一2 11 之1一之0 22 f。 物方空间 透镜(系统)区 像方空间 P=P. P可变 P=P, "=0 =0 (1) F F. 2) 21 22
20

计算这些量时,符号皆应保留,并注意其含义.如:焦距小于 0,意味着是散焦和虚焦点(好似光学凹透镜):位置计算值小于0, 则该点在参考点另一侧;单向放大率小于0,指像点与共轭物点在 之轴的异侧(180°翻转)一单个透镜作用、得实像往往如此:角放 大率恒与单向放大率同号:单个透镜的H。常在H之后或右侧, 称为“主平面交叉”. 推导要点 由矩阵链接 M=M,·M·M 满足成像条件时 M, 0 M,= 21 品 M 依次求轨迹(1)、(2)、(3)的'和/或',利用△=△'求位置 坐标. 最后满意地得到:以上量皆与。无关,即基点与外界无关.口
21