中国科学技术大学：《束流光学》课程教学资源（PPT课件讲稿）第二章 电子透镜

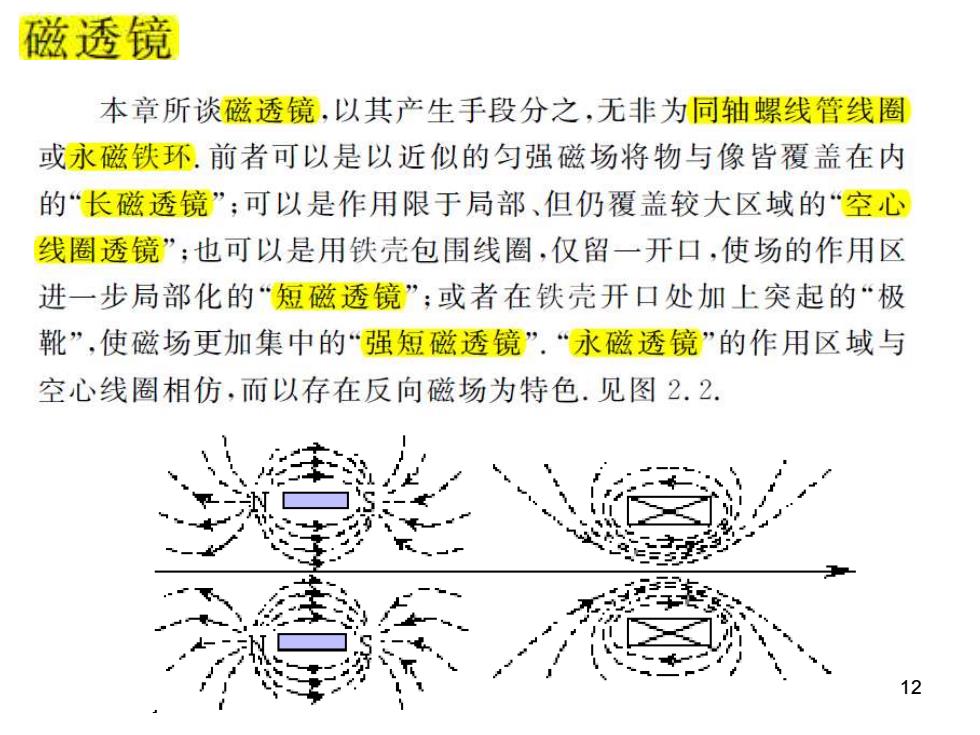
磁透镜 本章所谈磁透镜，以其产生手段分之，无非为同轴螺线管线圈 或永磁铁环.前者可以是以近似的匀强磁场将物与像皆覆盖在内 的“长磁透镜”；可以是作用限于局部、但仍覆盖较大区域的“空心 线圈透镜”：也可以是用铁壳包围线圈，仅留一开口，使场的作用区 进一步局部化的“短磁透镜”；或者在铁壳开口处加上突起的“极 靴”，使磁场更加集中的“强短磁透镜”.“永磁透镜”的作用区域与 空心线圈相仿，而以存在反向磁场为特色.见图2.2 12

12

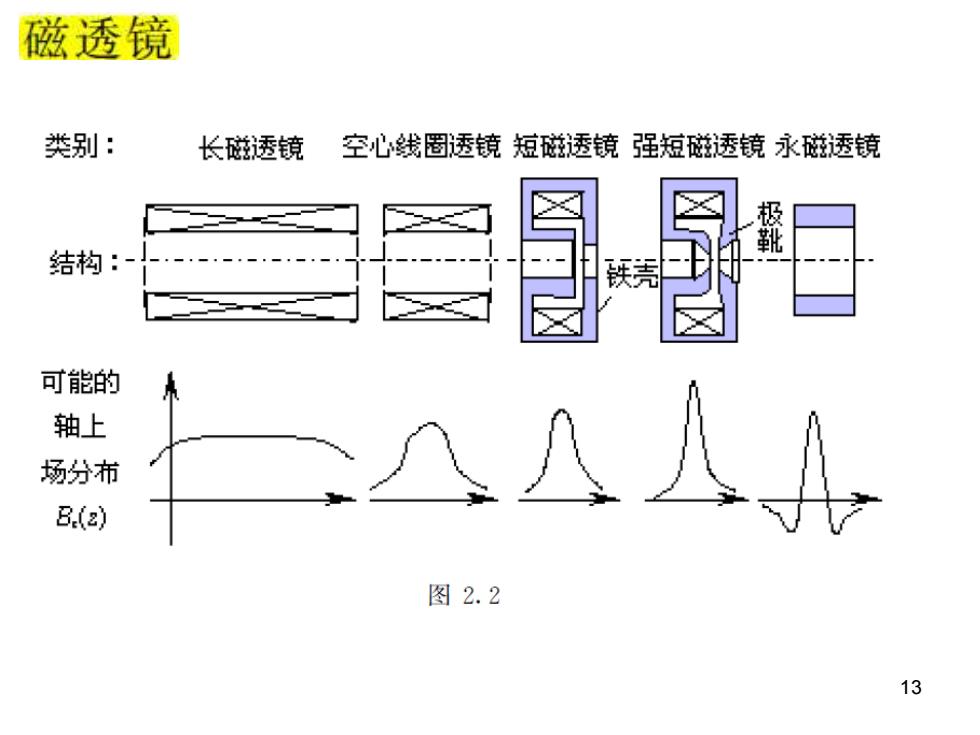
磁透镜 类别： 长磁透镜 空心线圈透镜短磁透镜强短磁透镜永磁透镜 结构： 可能的 轴上 场分布 八 B.() 图2.2 13

13

2.2 电子透镜的主要参量和传输矩阵、场分布 在几何光学中，常采用作图法，大致如图2.4所示.这相当于 以透镜为“薄透镜”，设∫为透镜的“焦距”，即镜平面到平行光在 “像方”的会聚点的距离，该透镜的作用矩阵元除m三二外皆 与单位矩阵相同 自由空间M=0 自由空-0] 事北疗梦 对于成像的情况仅和，有关而与式无关，所以儿(-月引L=0 卧非身身 几何光学处理“厚透镜”的方式复杂一些，要用到不止一个参 量.这些参量常称为透镜或光学系统的“基点

14       = 0 1 1 1 L 自由空间M         − = 1 1 1 0 2 f 薄透镜M             − − +        − − =          − −      =               −      = = f L f L f L L f L f L f L L L f L M M M M i i i i i 1 1 1 1 1 1 1 0 1 1 0 1 1 1 1 1 0 0 1 1 0 3 2 1          = − +  −          = −                    − −         − =       =       f L x f x x f L x x x x f L f f L x x M x x i i i i i 1 , 1 1 1 1 1 0 0 0 0 0 0 0 0 0       = 0 1 1 3 Li 自由空间M , 0 , 0 , 1 + = 0          − L f L 对于成像的情况 xi仅和x 有关 而与x 无关 所以Li             − −         − = f L f f L M i 1 1 1 1 0 0 L x0 xi f f Li

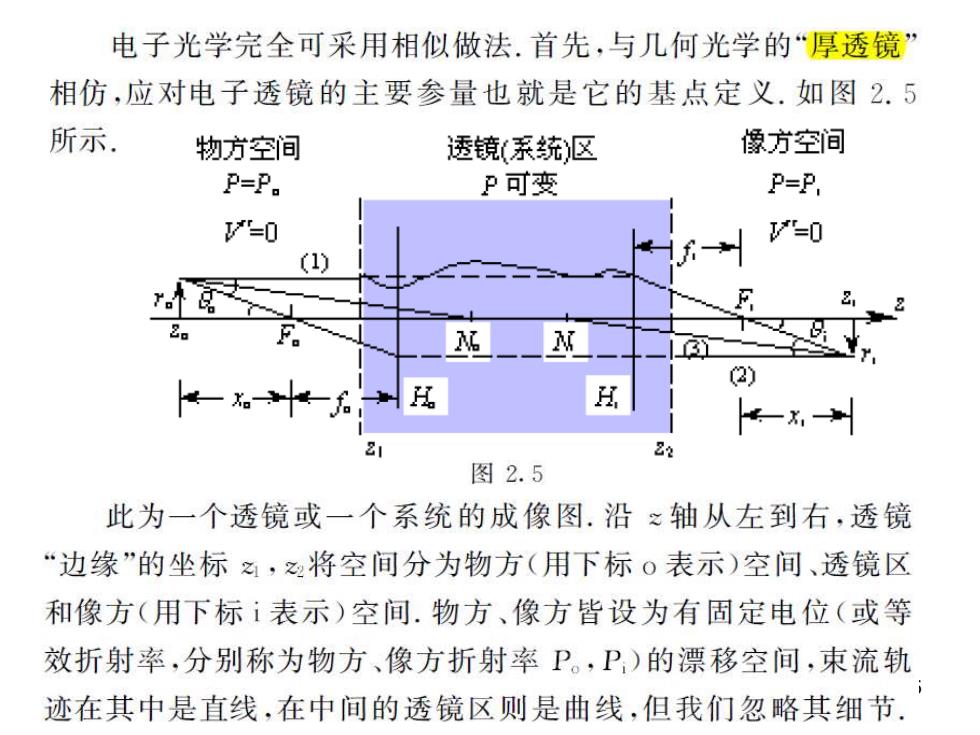
电子光学完全可采用相似做法.首先，与几何光学的“厚透镜” 相仿，应对电子透镜的主要参量也就是它的基点定义.如图2.5 所示. 物方空间 透镜（系统区 像方空间 P=P. P可变 P=P. "=0 "=0 (1) 2 F. 2) H 22 图2.5 此为一个透镜或一个系统的成像图.沿≈轴从左到右，透镜 “边缘”的坐标，将空间分为物方（用下标o表示）空间、透镜区 和像方（用下标ⅰ表示）空间.物方、像方皆设为有固定电位（或等 效折射率，分别称为物方、像方折射率P。,P)的漂移空间，束流轨 迹在其中是直线，在中间的透镜区则是曲线，但我们忽略其细节

15

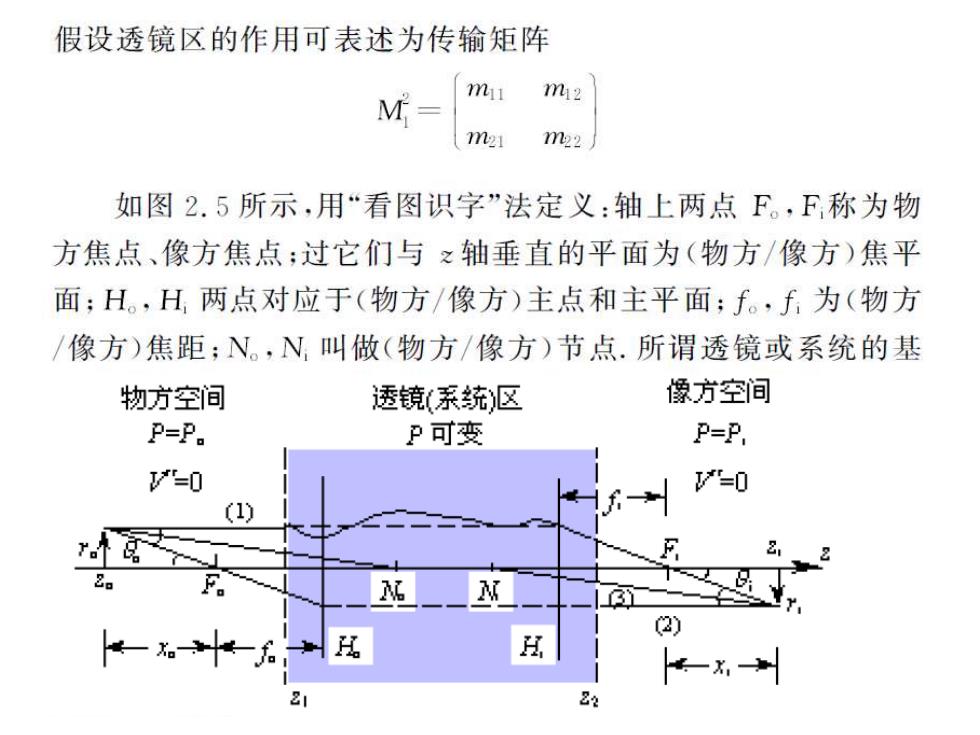
假设透镜区的作用可表述为传输矩阵 m m2 m21 m22 如图2.5所示，用“看图识字”法定义：轴上两点F。,F称为物 方焦点、像方焦点：过它们与之轴垂直的平面为（物方/像方）焦平 面；H。,H,两点对应于（物方/像方）主点和主平面；f。,f为（物方 /像方)焦距；N。,N叫做（物方/像方）节点.所谓透镜或系统的基 物方空间 透镜（系统）区 像方空间 P=P. P可变 P=P. "=0 =0 (1) 1- F. 2) H 2 22

16